| подавляющее большиство фукций на пространстве последовательостей? |
Рекурсия, итерация и оценки сложности алгоритмов
Более подробное изложение материала, рассматриваемого в данном параграфе, может быть найдено в книгах [9] и [4]. Вопросы, связанные с асимптотическими оценками сложности алгоритмов, подробно изложены в классической книге Кнута [6] и, охватывающем тематику двух первых курсов цикла программистских дисциплин, прекрасном издании [8].
Рекурсия и итерация
До сих пор мы рассматривали либо линейные программы, либо программы с ветвлениями, не требовавшими многократного повторения одних и тех же операций. Гораздо чаще, однако, приходится иметь дело именно с такими ситуациями. Существует два основных подхода к решению задач подобного типа: рекурсия и итерация.
Определение 5.1. Рекурсия — это такой способ организации обработки данных, при котором программа вызывает сама себя непосредственно, либо с помощью других программ.
Определение 5.2. Итерация — способ организации обработки данных, при котором определенные действия повторяются многократно, не приводя при этом к рекурсивным вызовам программ.
Математическая модель рекурсии заключается в вычислении рекурсивно определенной функции на множестве программных переменных. Примерами таких функций могут служить факториал числа и числа Фибоначчи. В каждом из этих случаев значение функции для всех значений аргумента, начиная с некоторого, определяется через предыдущие значения.
Факториал  ! целого неотрицательного числа
! целого неотрицательного числа  задается
следующими соотношениями:
задается
следующими соотношениями:
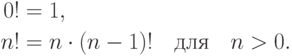
Числами Фибоначчи 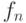 называют последовательность величин 0,
1, 1, 2, 3, 5,
8,
называют последовательность величин 0,
1, 1, 2, 3, 5,
8,  , определяемую равенствами:
, определяемую равенствами:

Математическая модель итерации сводится к повторению
некоторого преобразования (отображения)  на множестве переменных программы
на множестве переменных программы  (прямом произведении множеств
значений
отдельных переменных). Программной реализацией итерации является обычно
некоторый цикл, тело которого осуществляет преобразование
(прямом произведении множеств
значений
отдельных переменных). Программной реализацией итерации является обычно
некоторый цикл, тело которого осуществляет преобразование  .
.
В качестве примера можно рассмотреть схему вычисления факториала
натурального
числа в соответствии с его другим определением: 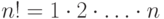 . При написании программы в соответствии с ним нужно работать с
двумя
величинами целого типа
. При написании программы в соответствии с ним нужно работать с
двумя
величинами целого типа 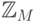 : числом
: числом  ,
которое будет играть роль
счетчика и изменяться от 1 до
,
которое будет играть роль
счетчика и изменяться от 1 до  включительно, и величиной
включительно, и величиной  , в которой
будет накапливаться произведение чисел от 1 до
, в которой
будет накапливаться произведение чисел от 1 до  .
.
Пространством  в данном случае будет
в данном случае будет  , в качестве
начальной точки в этом пространстве возьмем точку
, в качестве
начальной точки в этом пространстве возьмем точку 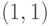 (что
соответствует
(что
соответствует 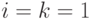 ), а преобразование
), а преобразование  будет
иметь вид
будет
иметь вид 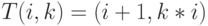 . В случае, например, трехкратного
применения преобразования
. В случае, например, трехкратного
применения преобразования  получим
получим 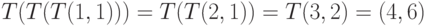 ,
что обеспечит вычисление факториала числа 3.
,
что обеспечит вычисление факториала числа 3.
Рекурсия и итерация взаимозаменяемы. Более точно, справедливо следующее утверждение.
Теорема 5.1. Любой алгоритм, реализованный в рекурсивной форме, может быть переписан в итерационном виде, и наоборот.
Данная теорема не означает, что временная и емкостная эффективности получающихся программ обязаны совпадать. Однако наилучшие рекурсивный и итерационный алгоритм имеют совпадающую с точностью до постоянного множителя временную сложность.
Особенности рекурсивных программ
Решая некоторую задачу, рекурсивный алгоритм вызывает сам себя для решения ее подзадач. Вот классический пример.
Задача 5.1. Напишите рекурсивную программу, вычисляющую факториал введенного натурального числа.
Текст программы
public class FactR {
static int f(int x) {
return (x == 0) ? 1 : x * f(x-1);
}
public static void main(String[] args) throws Exception {
Xterm.println("n!=" + f(Xterm.inputInt("n=")));
}
}Организация рекурсивных вычислений на языке Java не требует использования
никаких специальных конструкций — достаточно известного нам
вызова метода. В приведенной программе метод f
получает на вход целое число x и рекурсивно вычисляет его
факториал. Рассмотрим процесс выполнения данной программы для 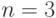 более
подробно.
более
подробно.
Вызов метода f с аргументом 3 представим в виде листа бумаги, на котором указано входное значение (число 3). Универсальный исполнитель должен выполнить предписанные действия на этом листе бумаги и получить итоговый результат. Так как число 3 отлично от нуля, универсальный исполнитель попытается умножить число 3 на f(2), но последняя величина для ее вычисления требует вызова метода f с аргументом 2.
В результате выполнение метода f с аргументом 3 приостановится и Универсальный исполнитель приступит к выполнению этого же метода с меньшим на единицу значением аргумента, что можно себе представить в виде еще одного листа бумаги, положенного на первый.
Вычисление f(2) потребует нахождения f(1), что вызовет появление еще одного листа бумаги — третьего экземпляра метода f. Он, в свою очередь, вызовет f(0). В этот момент накопится уже пачка листов (ее называют стеком вызовов ) — целых четыре штуки. При этом вычисления на всех нижних листах приостановлены до завершения работы с верхними.
Далее события будут развиваться следующим образом. Метод f, вызванный с нулевым аргументом, самостоятельно вычисляет и возвращает с помощью оператора return результат — число 1. Верхний элемент из стека вызовов методов после этого удаляется и возобновляются вычисления величины f(1). Этот процесс продолжается до тех пор, пока стек вызовов не станет пустым, что произойдет по завершению вычисления значения f(3). Итоговое значение 6 будет возвращено в метод main, который его и напечатает.
При написании рекурсивных программ обычно необходимо исследовать два основных вопроса:
а) всегда ли и почему программа заканчивает работу?
б) почему после окончания работы программы будет получен требуемый результат?
Подобное исследование для рассмотренной программы провести достаточно просто. Докажем по индукции, что эта программа заведомо завершит свою работу для всех целых неотрицательных чисел.
Рассмотрим следующее утверждение  , зависящее от числа
, зависящее от числа  : программа
завершает свою работу для входного значения
: программа
завершает свою работу для входного значения  за конечное время.
Для того чтобы доказать
истинность утверждения
за конечное время.
Для того чтобы доказать
истинность утверждения  для всех целых неотрицательных чисел
с помощью
метода математической индукции достаточно проверить его истинность при
нулевом значении
для всех целых неотрицательных чисел
с помощью
метода математической индукции достаточно проверить его истинность при
нулевом значении  (база индукции) и убедиться в справедливости
индуктивного
перехода, что требует проверки истинности предиката
(база индукции) и убедиться в справедливости
индуктивного
перехода, что требует проверки истинности предиката 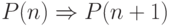 .
.
При нулевом значении аргумента программа завершает свою работу немедленно,
поэтому утверждение  истинно и база индукции проверена.
истинно и база индукции проверена.
Пусть утверждение  истинно при некотором значении
истинно при некотором значении  . Покажем, что и
. Покажем, что и 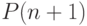 тогда истинно. Для вычисления f(n+1) в соответствии
с текстом
программы нужно перемножить n+1 и f(n). Истинность
тогда истинно. Для вычисления f(n+1) в соответствии
с текстом
программы нужно перемножить n+1 и f(n). Истинность  гарантирует нам вычисление второго множителя за конечное время, а так как
перемножение двух чисел тоже требует конечного времени, то и
гарантирует нам вычисление второго множителя за конечное время, а так как
перемножение двух чисел тоже требует конечного времени, то и 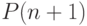 истинно,
что и завершает доказательство завершения работы программы при всех целых
неотрицательных значениях аргумента.
истинно,
что и завершает доказательство завершения работы программы при всех целых
неотрицательных значениях аргумента.
Заметим, что для отрицательных значений 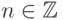 данная
программа
должна была бы работать бесконечно долго (как принято говорить, должна зациклиться ). Однако из-за того, что в реальности мы имеем дело с
машинным заменителем множества целых чисел — множеством
данная
программа
должна была бы работать бесконечно долго (как принято говорить, должна зациклиться ). Однако из-за того, что в реальности мы имеем дело с
машинным заменителем множества целых чисел — множеством 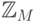 ,
выполнение всегда завершится за конечное время, хотя полученный результат
и не будет иметь никакого смысла.
,
выполнение всегда завершится за конечное время, хотя полученный результат
и не будет иметь никакого смысла.
Доказательство правильности вычисляемого приведенной программой значения
проводится совершенно аналогично. Рассмотрим утверждение 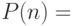 ( для входного значения
( для входного значения  результатом является
результатом является  !) и
докажем его истинность по индукции.
!) и
докажем его истинность по индукции.
Истинность  (база индукции) проверяется непосредственно, а
для проверки
корректности индуктивного перехода напишем следующую цепочку равенств:
(база индукции) проверяется непосредственно, а
для проверки
корректности индуктивного перехода напишем следующую цепочку равенств: 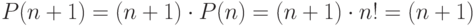 !, первое из
которых следует
из текста программы, второе — из предположения индукции, а третье — из
определения факториала. Это завершает доказательство теоретической
правильности написанной программы.
!, первое из
которых следует
из текста программы, второе — из предположения индукции, а третье — из
определения факториала. Это завершает доказательство теоретической
правильности написанной программы.
В реальности,
однако, быстрый рост функции  ! и ограниченность множества
! и ограниченность множества 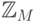 приводят к тому, что эта программа позволяет получить
правильные результаты только при очень небольших значениях
приводят к тому, что эта программа позволяет получить
правильные результаты только при очень небольших значениях  . Уже
при
. Уже
при 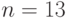 печатаемое ей значение 1932053504 отличается от правильного 6227020800, а при
печатаемое ей значение 1932053504 отличается от правильного 6227020800, а при 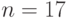 программа выдает даже отрицательный результат!
программа выдает даже отрицательный результат!
Рассмотрим еще одну задачу.
Задача 5.2. Напишите рекурсивную программу, печатающую  -ое число Фибоначчи.
-ое число Фибоначчи.
Текст программы
public class FibR {
static int fib(int x) {
return (x > 1) ? fib(x-2) + fib(x-1) : (x == 1) ? 1 : 0;
}
public static void main(String[] args) throws Exception {
int n = Xterm.inputInt("Введите n -> ");
Xterm.println("fib(" + n + ") = " + fib(n));
}
}Обратите внимание, что при вычислении 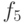 в соответствии с
этой программой
понадобится найти
в соответствии с
этой программой
понадобится найти 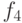 и
и 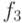 . Определение
. Определение 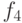 , в свою очередь, потребует
вычисления
, в свою очередь, потребует
вычисления 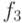 и
и  , и так далее. Внимательно
изучение содержимого стека
вызовов для этой задачи показывает, что для нахождения каждого следующего
числа Фибоначчи требуется примерно вдвое большее время,
чем для определения предыдущего. Для того, чтобы убедиться в этом, нарисуйте
дерево, изображающее процесс вычисления
, и так далее. Внимательно
изучение содержимого стека
вызовов для этой задачи показывает, что для нахождения каждого следующего
числа Фибоначчи требуется примерно вдвое большее время,
чем для определения предыдущего. Для того, чтобы убедиться в этом, нарисуйте
дерево, изображающее процесс вычисления 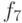 с помощью данной
программы.
с помощью данной
программы.
