| подавляющее большиство фукций на пространстве последовательостей? |
Изображение полиэдра
Этот параграф посвящен рассмотрению еще одного проекта, который позволит познакомиться с простейшими задачами вычислительной геометрии. Построение изображения полиэдра с удалением невидимых линий — пример столь же классической задачи, как и рассмотренная в предыдущем параграфе задача компиляции. В процессе работы над проектом происходит также знакомство с графической библиотекой (пакетом) AWT и системой документирования программ javadoc.
В книгах [9] и [8] содержится большое количество дополнительной информации, связанной с рассматриваемой задачей и ее различными обобщениями. Вопросы работы с пакетом AWT и системой документирования в языке Java более подробно могут быть изучены с помощью книг [11] и [10] .
Постановка задачи
В настоящее время во многих областях науки и техники используются различные методы моделирования геометрических объектов в трехмерном пространстве. Один из способов моделирования состоит в том, чтобы аппроксимировать реальный объект набором выпуклых плоских многоугольников. Такой набор мы будем называть полиэдром , многоугольники — гранями, а их стороны — ребрами полиэдра.
Примерами полиэдров могут служить поверхности куба, призмы и пирамиды (включая усеченную), листы полураскрытой веером книги и даже просто два-три выпуклых многоугольника, расположенных в трехмерном пространстве друг относительно друга произвольным образом.
При изображении полиэдра реально рисуются не сами многоугольники, а линии, их ограничивающие, то есть их ребра. Если, однако, изобразить все ребра полиэдра, то получится весьма запутанная, непривычная для человека картина. Для получения удобного для человека рисунка нужно при построении изображения учитывать, что некоторые ребра могут оказаться полностью или частично невидимыми, так как их могут загородить грани полиэдра. Таким образом, при построении изображения надо удалить (не рисовать) части ребер, которые не видны. По этой причине рассматриваемая задача в литературе часто называется задачей удаления невидимых линий.
Задача 13.1. Напишите программу, которая строит изображение заданного полиэдра с удалением невидимых линий. Программа должна быть реализована в виде автономного приложения на языке Java и использовать возможности пакета AWT.
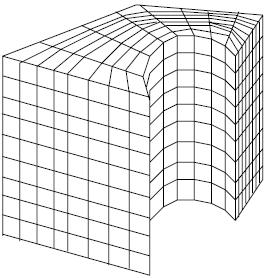
В результате решения этой задачи полиэдр должен изображаться примерно так, как это показано на рис. 13.1.
Изображение полиэдра зависит от того, откуда на него посмотреть. Это направления должно быть задано в точной постановке задачи. Направление, противоположное направлению взгляда, будем называть вектором проектирования и считать, что он направлен вверх. Этого всегда можно добиться, осуществив поворот полиэдра вместе с заданным вектором проектирования. Для того чтобы упростить терминологию, договоримся называть в дальнейшем параллельные вектору проектирования прямые и плоскости вертикальными, а ортогональные ему — горизонтальными.
Рассматриваемая задача, таким образом, сводится к следующей: построить
проекцию полиэдра с удалением невидимых линий на бесконечно высокую
горизонтальную плоскость 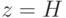 . Требуемое плоское изображение при
этом задано
не однозначно, так как вращения вокруг вертикальной оси
. Требуемое плоское изображение при
этом задано
не однозначно, так как вращения вокруг вертикальной оси 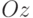 приводят к
поворотам итоговой картинки. Будем поэтому считать, что полная постановка
задачи кроме самого полиэдра и вектора проектирования содержит также задание
угла поворота в плоскости проекции.
приводят к
поворотам итоговой картинки. Будем поэтому считать, что полная постановка
задачи кроме самого полиэдра и вектора проектирования содержит также задание
угла поворота в плоскости проекции.
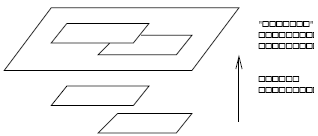
Такую уточненную постановку задачи иллюстрирует рис. 13.2.
Способ задания вектора проектирования и угла поворота в плоскости проекции вполне ясен, а вот как следует задавать полиэдр нужно обсудить. Простейший способ — перечисление координат всех вершин каждой из его граней. В силу ряда недостатков такого представления, однако, этот способ на практике не применяется.
Достаточно часто при задании полиэдра всю информацию о нем разделяют на две части. Первая из них задает так называемый абстрактный полиэдр. При этом определяется только количество граней, ребер и вершин в нем с указанием того, какие именно ребра принадлежат отдельным граням, а вершины — ребрам. Вторая часть информации, называемая метрической, определяет координаты всех вершин полиэдра в пространстве.
Способ представления полиэдра, который будет использован нами при решении рассматриваемой задачи, несколько отличен от только что описанного. Он предусматривает указание числа и координат вершин полиэдра, а также количества граней и ребер с указанием для каждой из граней номеров всех ее вершин. По этой причине многие ребра оказываются указанными дважды или даже большее число раз (так как принадлежат нескольким граням), что является, безусловно, недостатком этого способа представления.
Этот способ задания полиэдра, тем не менее, является достаточно удобным и распространенным, а устранение его негативных последствий будет предложено в конце параграфа в виде задачи для самостоятельного решения.
Информация, представляющая полиэдр, является достаточно объемной, и поэтому было бы весьма неудобно вводить ее, используя клавиатуру. Гораздо разумнее создать описание полиэдра в специальном файле, а программе передать его имя. Вот как будет выглядеть этот файл, представляющий поверхность единичного куба с центром в начале координат и гранями, параллельными координатным плоскостям:
8 6 24
-0.5 -0.5 0.5
-0.5 0.5 0.5
0.5 0.5 0.5
0.5 -0.5 0.5
-0.5 -0.5 -0.5
-0.5 0.5 -0.5
0.5 0.5 -0.5
0.5 -0.5 -0.5
4 1 2 3 4
4 5 6 2 1
4 3 2 6 7
4 3 7 8 4
4 1 4 8 5
4 8 7 6 5Первая строка говорит о том, что у куба 8 вершин, 6 граней и 24 (!) ребра. Число 24, вдвое превышающее реальное количество ребер у куба, является результатом уже описанного выше эффекта, — каждое из ребер куба принадлежит ровно двум граням.
Следующая часть файла содержит метрическую информацию — координаты всех восьми вершин полиэдра, а в заключительной части файла для каждой из шести граней куба указываются количество ее вершин и перечисляются их номера.
Технические детали работы с файлами и чтения информации из них могут быть изучены заинтересованными читателями самостоятельно с использованием итогового текста проекта, приведенного в конце параграфа, и литературы, содержащей описание библиотек (пакетов) языка Java.
Проектирование основных классов
В данной секции будет построена иерархия классов, необходимых для реализации рассматриваемого проекта. Здесь же мы рассмотрим (в самых общих чертах) использование библиотеки AWT программами, не являющимися аплетами.
Класс R3Vector позволит задать произвольный вектор и обеспечит все необходимые манипуляции над векторами в трехмерном пространстве. Полный набор методов, которые должен реализовывать класс R3Vector, выяснится в процессе дальнейшего решения задачи. Пока же заметим, что вектор проектирования, являющийся экземпляром класса R3Vector, должен вводиться с клавиатуры, и предусмотрим дополнительный конструктор специально для этих целей.
public class R3Vector {
private double x, y, z;
public R3Vector(double x, double y, double z) {
this.x = x; this.y = y; this.z = z;
}
public R3Vector() throws Exception {
x = Xterm.inputDouble("X-коорд. вектора проектирования -> ");
y = Xterm.inputDouble("Y-коорд. вектора проектирования -> ");
z = Xterm.inputDouble("Z-коорд. вектора проектирования -> ");
}
}Для представления вершин полиэдра можно использовать выведенный из класса R3Vector класс Vertex. Конструктор данного класса обязан явным образом (с помощью ключевого слова super ) вызвать конструктор его базового класса R3Vector, так как иначе компилятор автоматически вставит вызов конструктора класса R3Vector без параметров.
public class Vertex extends R3Vector {
public Vertex(double x, double y, double z) {
super(x, y, z);
}
}Ребра полиэдра будем представлять с помощью класса Edge, в каждом экземпляре которого содержатся две private -компоненты типа Vertex, соответствующие началу и концу ребра. В подобных ситуациях для обеспечения возможности получения координат начала и конца ребра используют так называемые методы-селекторы getBegin и getEnd.
public class Edge {
private Vertex begin;
private Vertex end;
public Edge(Vertex begin, Vertex end) {
this.begin = begin; this.end = end;
}
public final Vertex getBegin() {
return begin;
}
public final Vertex getEnd() {
return end;
}
}Грани полиэдра будем описывать с помощью класса Facet. Так как грань задается последовательностью ее вершин, то в каждом экземпляре класса должен содержаться массив объектов типа Vertex, для получения количества и координат которых необходимо предусмотреть соответствующие методы.
public class Facet {
private Vertex[] vertexes;
public Facet(Vertex[] vertexes) {
this.vertexes = vertexes;
public final int getVertexesQuantity() {
return vertexes.length;
}
public final Vertex getVertex(int i) {
return vertexes[i];
}Полиэдр в целом, наконец, будем задавать с помощью класса Polyedr. Каждый экземпляр этого класса будет хранить в массивах vertexes, edges и facets все вершины, ребра и грани полиэдра. При этом оказывается, что часть информации хранится продублированной, так как каждая из граней полиэдра уже содержит все ее вершины. Устранение этого дублирования является еще одной из задач, предлагаемых в конце параграфа.
При создании нового экземпляра класса Polyedr с помощью конструктора вся информация о полиэдре, хранящаяся в файле file в описанном выше формате, должна быть прочитана из него и размещена должным образом в компонентах создаваемого экземпляра. Для реализации этих действий необходимо использование пакетов java.util и java.io, что обуславливает необходимость наличия директив import в начале файла. Все технические детали осуществления чтения информации из файла оставляются читателю, а полный исходный текст проектируемого класса приведен для справки в последней секции параграфа.
import java.util.*;
import java.io.*;
public class Polyedr {
private Vertex[] vertexes;
private Edge[] edges;
private Facet[] facets;
public Polyedr(String file) throws Exception {
...
}
public final int getVertexesQuantity() {
return vertexes.length;
}
public final Vertex getVertex(int i) {
return vertexes[i];
}
public final int getEdgesQuantity() {
return edges.length;
}
public final Edge getEdge(int i) {
return edges[i];
}
public final int getFacetsQuantity() {
return facets.length;
}
public final Facet getFacet(int i) {
return facets[i];
}
}