| подавляющее большиство фукций на пространстве последовательостей? |
Спецификация программ и преобразователь предикатов
Важнейший для дальнейшего изучения материал этого параграфа в более подробном изложении можно найти в книге [4]. Полезным будет также и знакомство с подходом учебного пособия [9].
Предикаты и документирование программ
Как уже отмечалось выше, предикаты нам нужны прежде всего для того, чтобы иметь возможность ясно и недвусмысленно формулировать определенные утверждения о программах и программных переменных. Сейчас мы рассмотрим ряд примеров подобного типа.
Задача 6.1. Запишите предикат, утверждающий, что
если  , а
, а  , то
, то  .
.
Решение. В данном случае все очевидно:  .
.
Задача 6.2. Запишите предикат, утверждающий, что
ни одно из следующих утверждений не является истинным:  ,
,  и
и 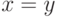 .
.
Решение Это задание тоже не является сложным. Вот несколько эквивалентных между
собой решений:  ,
,  и
и 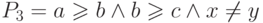 . Так как
обычно нужно
предъявить максимально простой предикат, то будем считать ответом последний
из них —
. Так как
обычно нужно
предъявить максимально простой предикат, то будем считать ответом последний
из них —  .
.
В ряде последующих задач нам придется иметь дело с массивами, поэтому
договоримся о следующих обозначениях: будем обозначать вырезку из
массива ![b[0..m-1]](/sites/default/files/tex_cache/4076bda9f74e4a0083e3d3e407de4f68.png) , в которой содержатся все элементы данного
массива с
индексами от
, в которой содержатся все элементы данного
массива с
индексами от  до
до  включительно, символом
включительно, символом ![b[j..k]](/sites/default/files/tex_cache/3b3b31473e43560c64c3e2a946b7f1b8.png) . В случаях, когда
. В случаях, когда  ,
,  или
или  , вырезка
представляет из себя пустое множество.
, вырезка
представляет из себя пустое множество.
Задача 6.3.Запишите предикат, утверждающий, что
для массива ![b[0..n-1]](/sites/default/files/tex_cache/f0d2d66a2d25c9d587516c612208e85d.png) длины
длины  все элементы вырезки
все элементы вырезки ![b[j..k]](/sites/default/files/tex_cache/3b3b31473e43560c64c3e2a946b7f1b8.png) являются нулевыми.
являются нулевыми.
Решение.
Используем квантор всеобщности: ![\forall i\ j\leqslant i<k+1\ b[i]=0](/sites/default/files/tex_cache/20fc86688042280f46d570de3c992cbc.png) .
.
Задача 6.4.Запишите предикат, утверждающий, что
для массива ![b[0..n-1]](/sites/default/files/tex_cache/f0d2d66a2d25c9d587516c612208e85d.png) длины
длины  ни один из элементов вырезки
ни один из элементов вырезки ![b[j..k]](/sites/default/files/tex_cache/3b3b31473e43560c64c3e2a946b7f1b8.png) не нулевой.
не нулевой.
Решение.
Переформулировав данное высказывание (все элементы вырезки не нулевые),
запишем ответ в следующем виде: ![\forall i\ j\leqslant i<k+1\ b[i]\ne
0](/sites/default/files/tex_cache/70e941380c2582db10e70aa143956722.png) .
.
Задача перевода высказывания с естественного языка на язык предикатов не всегда является однозначной, но именно это и является одной из причин его использования. Вот пример.
Задача 6.5. Запишите предикат, утверждающий, что
для массива ![b[0..n-1]](/sites/default/files/tex_cache/f0d2d66a2d25c9d587516c612208e85d.png) длины
длины  некоторые из элементов вырезки
некоторые из элементов вырезки ![b[j..k]](/sites/default/files/tex_cache/3b3b31473e43560c64c3e2a946b7f1b8.png) нулевые.
нулевые.
Решение.
Данное высказывание можно понимать двояко: оно может означать, что в вырезке
существует хотя бы один нулевой элемент, а может значить и то, что в ней как
минимум два нулевых элемента. Вот ответы для каждого из этих вариантов
трактовки задачи: ![P_1 = \exists i\ j\leqslant i<k+1\ b[i]=0](/sites/default/files/tex_cache/fe06ac331e47a0d7899c5f1ae134f181.png) и
и ![P_2 = \exists i\ j\leqslant i<k+1\
\exists m\ (j\leqslant m<k+1 \land m \ne i) (b[i]=0)\land (b[m]=0)](/sites/default/files/tex_cache/9bb526b1eeca808536784782908644b7.png) .
.
Вот аналогичные задачи из области математики.
Задача 6.6. Запишите предикат, который утверждает, что функция  является сюръективной и отрицание этого факта.
Упростите получившиеся предикаты, если это возможно.
является сюръективной и отрицание этого факта.
Упростите получившиеся предикаты, если это возможно.
Решение.
В соответствии с определением сюръективности имеем  .
Построим отрицание и упростим его в соответствии с законами эквивалентности.
.
Построим отрицание и упростим его в соответствии с законами эквивалентности.  .
.
Задача 6.7. Запишите предикат, который утверждает, что функция  все элементы, не превосходящие трех, не
увеличивает, и отрицание этого факта.
Упростите получившиеся предикаты, если это возможно.
все элементы, не превосходящие трех, не
увеличивает, и отрицание этого факта.
Упростите получившиеся предикаты, если это возможно.
Решение.  . Его отрицание
можно
упростить:
. Его отрицание
можно
упростить:  .
.
В текст программы зачастую полезно включать предикаты, которые позволяли бы человеку или компьютеру проверять корректность хода выполнения программы. В тех случаях, когда подобные утверждения предназначены только для человека, они оформляются в виде комментариев.
Часто, однако, полезно поручить проверку истинности предикатов в процессе выполнения программы непосредственно компьютеру. В различных языках программирования эта возможность реализована по-разному. Например, в программах на языке C можно использовать макрос assert(P), который в случае ложности его аргумента (предиката P ) немедленно прекращает выполнение программы, сообщая о причине этого.
Механизм работы с исключениями и оператор if позволяют легко реализовать аналогичную конструкцию в языке Java. Вот простейший пример.
Задача 6.8. Напишите программу, содержащую проверку истинности утверждения о положительности введенного с клавиатуры целого числа.
Текст программы
public class Assert {
public static void main(String[] args) throws Exception {
int n = Xterm.inputInt("Введите n -> ");
if (n <= 0)
throw new Exception("n <= 0");
Xterm.println("n = " + n);
}
}При вводе неположительного числа программа прекращает свое выполнение и печатает следующий текст:
java.lang.Exception: n<=0
at Assert.main(Assert.java:4)Богатые возможности работы с исключениями, имеющиеся в языке, позволяют реализовать гораздо более изощренные способы проверки истинности предикатов, нежели использованный в программе простейший вариант возбуждения исключения типа Exception без попыток его последующей обработки. Эти возможности, однако, не будут рассматриваться в нашем курсе.
