| подавляющее большиство фукций на пространстве последовательостей? |
Высказывания и предикаты
Материал этого и некоторых из следующих параграфов в значительной мере основан на подходе к программированию, применяемом в книге [4], знакомство с которой весьма полезно. Что же касается собственно математической теории предикатов, то нам необходимы только ее основы, и поэтому обращение к какой-либо специальной дополнительной литературе по этой тематике не требуется.
Зачем программисту предикаты
Все знают, что в программах бывают ошибки (bugs). Существуют специальные теории, посвященные тому, как лучше их находить и исправлять ( debugging дословно означает "выведение клопов"). Зачастую нахождение ошибки — очень нетривиальная задача, так как ее последствия могут сказываться совершенно в другом месте программы и быть весьма неожиданными.
При этом часто забывается тот очевидный факт, что ошибку гораздо легче предотвратить при написании программы, нежели найти и исправить потом. Существуют методы проектирования программ (по крайней мере, небольших), позволяющие не только написать правильную программу, но и получить одновременно с этим совершенно строгое доказательство ее правильности. Изучению таких методов и будет посвящена в основном вторая глава данной книги.
Однако для того, чтобы изучить какую-либо теорию, необходимо выучить язык, на котором теория может быть изложена. Язык предикатов — это именно тот язык, на котором можно строго сформулировать постановку задачи и доказать правильность конкретной программы. Попробуйте решить следующую задачу.
Задача 3.1. Задача о банке с кофейными зернами. В банке имеется несколько черных и белых кофейных зерен. Следующий процесс надо повторять, пока это возможно:
- случайно выберите из банки два зерна и
- если они одного цвета, отбросьте их, но положите в банку другое черное зерно (имеется достаточный запас черных зерен, чтобы делать это);
- если они разного цвета, поместите белое зерно обратно в банку и отбросьте черное зерно.
Выполнение этого процесса уменьшает количество зерен в банке на единицу. Повторение процесса должно прекратиться, когда в банке останется всего одно зерно, так как тогда нельзя уже выбрать два зерна. Можно ли что-то сказать о цвете оставшегося зерна, если известно, сколько вначале в банке было черных и белых зерен?
Попытка решать эту задачу, используя тестовые примеры с небольшим начальным количеством зерен в банке, не приводит ни к какому результату в течение значительного промежутка времени. Этот подход к решению является в каком-то смысле аналогом тестирования программы с целью выявления ошибок в ней.
Знание теории позволяет получить ответ на вопрос задачи почти мгновенно, однако объяснить это решение практически невозможно без привлечения такого понятия, как инвариант цикла, речь о котором пойдет в нашем курсе значительно позже. Инвариант цикла — это предикат, обладающий некоторыми специальными свойствами. Интересно, что при этом даже пятиклассник может справиться с рассматриваемой задачей, решив ее как-то. Под этим понимается по существу правильное решение, правильность которого доказать абсолютно невозможно.
Теперь рассмотрим вопрос о том, насколько сложно протестировать уже написанную программу. При этом мы будем предполагать для простоты, что для линейной программы (без ветвлений) достаточно всего одного теста, для программы с одним оператором if — двух (чтобы протестировать правильность каждой из его ветвей) и так далее.
Реальные большие программы, конечно, не сводятся к совокупности вложенных друг в друга условных операторов. Однако они не проще, а сложнее — ведь в них есть и циклы и вызовы функций, подпрограмм или методов, обработка исключительных ситуаций и многое другое.
Вернемся к нашей модели. Если в программе 10 операторов if, то нужно
выполнить  теста, а если их 20, то уже
теста, а если их 20, то уже  !
Можно ли надеяться на то, что в процессе тестирования реальной большой
программы удастся проверить все возможные варианты ее работы? Нет, конечно.
Именно поэтому так важно не делать ошибок, так как потом их скорее всего
просто не обнаружить.
!
Можно ли надеяться на то, что в процессе тестирования реальной большой
программы удастся проверить все возможные варианты ее работы? Нет, конечно.
Именно поэтому так важно не делать ошибок, так как потом их скорее всего
просто не обнаружить.
В заключение поговорим о правильности большой программы,
состоящей из многих
небольших частей. Предположим, что для каждой из этих частей мы можем
гарантировать правильность ее работы с вероятностью 99%. Это значит, что
в среднем только в одном случае из ста что-то может быть не так, а в 99
случаях каждая часть будет работать абсолютно правильно. Пусть всего таких
частей  . Какова вероятность правильной работы программы в целом?
. Какова вероятность правильной работы программы в целом?
Это — простейшая задача по курсу теории вероятностей и ответ у нее такой:  . Здесь
. Здесь  — вероятность правильной работы
каждой из частей, а
— вероятность правильной работы
каждой из частей, а  — вероятность правильной работы программы в целом. При
— вероятность правильной работы программы в целом. При 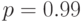 получаем результаты, приведенные в таблице 3.1.
получаем результаты, приведенные в таблице 3.1.
| n | 10 | 100 | 1000 |
| P | 0.904 | 0.366 | 0.00004 |
При 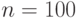 программа будет работать правильно чуть более, чем в
одной трети
всех ситуаций, а при
программа будет работать правильно чуть более, чем в
одной трети
всех ситуаций, а при 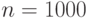 увидеть ее работающей вообще вряд ли
удастся.
Этот пример показывает, что нужно всеми силами стараться избегать написания почти правильных программ!
увидеть ее работающей вообще вряд ли
удастся.
Этот пример показывает, что нужно всеми силами стараться избегать написания почти правильных программ!
