| подавляющее большиство фукций на пространстве последовательостей? |
Индуктивные функции на пространстве последовательностей
Решим еще одну задачу.
Задача 9.3. Напишите программу, вводящую последовательность вещественных чисел, и печатающую среднее арифметическое ее элементов (для непустой последовательности).
Решение
По условию задачи 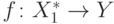 , где
, где 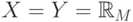 .
Если
.
Если 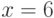 ,
, 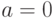 ,
, 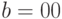 (цепочка из двух
нулей), то
(цепочка из двух
нулей), то 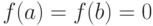 , но
, но 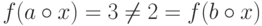 ,
следовательно
,
следовательно  не является индуктивной.
не является индуктивной.
Построим ее индуктивное расширение  .
Обозначив через
.
Обозначив через 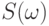 сумму элементов последовательности
сумму элементов последовательности  ,
получаем
,
получаем 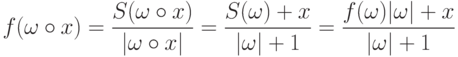 .
Следовательно, в качестве
.
Следовательно, в качестве 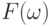 можно взять пару
можно взять пару  .
Для
.
Для 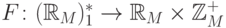 ,
где
,
где 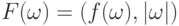 , преобразование
, преобразование 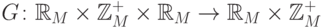 задается формулой
задается формулой  .
.
Проектируемая программа будет проще, если мы сможем продолжить  на
на 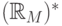 с сохранением
с сохранением  . Попробуем
подобрать подходящую пару
. Попробуем
подобрать подходящую пару 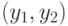 такую, чтобы
такую, чтобы 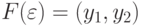 и
и 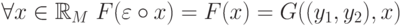 . Так как
. Так как 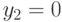 ,
то из последнего равенства получаем
,
то из последнего равенства получаем 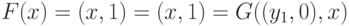 ,
что справедливо при всех
,
что справедливо при всех  . Следовательно, можно
положить,
например,
. Следовательно, можно
положить,
например, 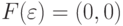 . Теперь
. Теперь 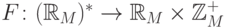 .
Отображение
.
Отображение 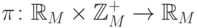 тривиально:
тривиально:  , а
построенное нами расширение не является минимальным, так как значение
, а
построенное нами расширение не является минимальным, так как значение 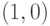 функцией
функцией  не принимается.
не принимается.
Текст программы
public class AverSeq{
public static void main(String[] args) {
double y1 = 0., y2 = 0.;
try {
while (true) {
double x = Xterm.inputDouble("x -> ");
y1 = (y1*y2 + x) / (y2 + 1.);
y2 += 1;
}
} catch(Exception e) {
Xterm.println("\nf = " + y1);
}
}
}Рассмотрим задачу несколько другого типа.
Задача 9.4. Напишите программу, определяющую количество вхождений
образца  в последовательность символов.
в последовательность символов.
Решение
Пусть  — множество всех символов, тогда функция
— множество всех символов, тогда функция 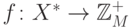 . Если
. Если 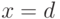 ,
, 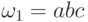 ,
, 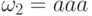 , то
, то 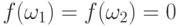 , но
, но 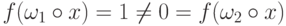 , следовательно
, следовательно  не является
индуктивной.
не является
индуктивной.
Заметив, что 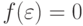 , будем строить ее индуктивное
расширение.
, будем строить ее индуктивное
расширение.
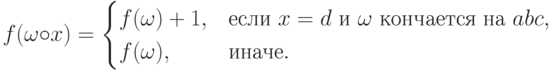
Введем дополнительную функцию 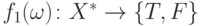 ,
которая будет истинна только тогда, когда
,
которая будет истинна только тогда, когда  кончается на
кончается на  , и
рассмотрим функцию
, и
рассмотрим функцию  . Для нее имеем
. Для нее имеем  ,
,
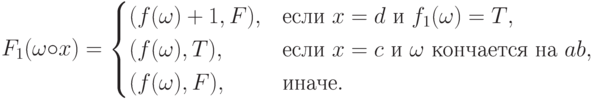
Необходимо ввести еще одну дополнительную функцию 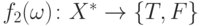 ,
которая будет истинна только тогда, когда
,
которая будет истинна только тогда, когда  кончается на
кончается на  .
Теперь можно рассмотреть
.
Теперь можно рассмотреть 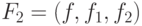 . Для нее имеем
. Для нее имеем 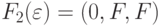 ,
,
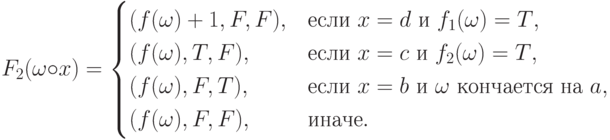
Так как нам опять не удалось выразить 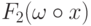 только через
только через 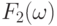 и
и  , придется рассмотреть еще одну
функцию
, придется рассмотреть еще одну
функцию 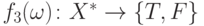 ,
которая будет истинна только тогда, когда
,
которая будет истинна только тогда, когда  кончается на
кончается на  .
Для функции
.
Для функции 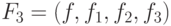 , действующей в пространство
, действующей в пространство 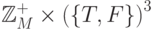 получаем
получаем 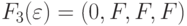 ,
,
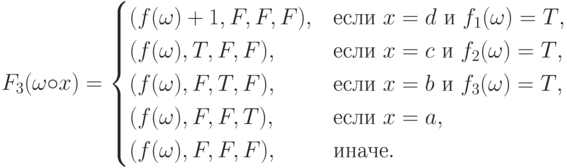
Полученное равенство показывает, что 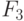 — индуктивное
расширение
— индуктивное
расширение  ,
однако оно достаточно сложно и заведомо не является минимальным, так как
,
однако оно достаточно сложно и заведомо не является минимальным, так как 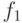 ,
,  и
и 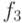 не являются
независимыми. У тройки величин
не являются
независимыми. У тройки величин 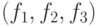 имеется всего четыре допустимых состояния, которые
можно представить одним числом:
имеется всего четыре допустимых состояния, которые
можно представить одним числом:

Сейчас мы докажем, что функция 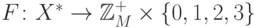 ,
определенная соотношением
,
определенная соотношением 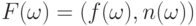 является минимальным индуктивным расширением
является минимальным индуктивным расширением  .
.
Для доказательства индуктивности достаточно предъявить преобразование 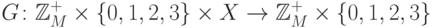 :
:
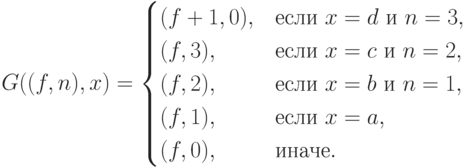
Для доказательства
сюръективности функции  предъявим прообраз произвольного
элемента
предъявим прообраз произвольного
элемента 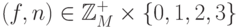 . Им может служить, например,
цепочка,
начинающаяся с
. Им может служить, например,
цепочка,
начинающаяся с  вхождений образца
вхождений образца  , за которым
следует еще
, за которым
следует еще  первых символов этого образца. Для того чтобы проверить
второе условие критерия минимальности, необходимо убедиться в том, что
первых символов этого образца. Для того чтобы проверить
второе условие критерия минимальности, необходимо убедиться в том, что  .
.
Пусть 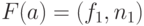 ,
, 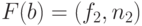 и
либо
и
либо 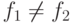 , либо
, либо  . Если
. Если 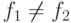 , то в качестве
, то в качестве  можно взять пустую цепочку.
В противном случае без ограничения общности
можно считать, что
можно взять пустую цепочку.
В противном случае без ограничения общности
можно считать, что  . Цепочка
. Цепочка  заканчивается на
заканчивается на 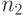 первых
символа образца
первых
символа образца  , поэтому если в качестве
, поэтому если в качестве  взять
взять  последних символа
этого образца, то
последних символа
этого образца, то 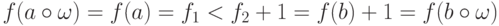 , что и завершает доказательство
минимальности
, что и завершает доказательство
минимальности  .
.
Текст программы
import java.io.*;
public class ABCDSeq {
public static void main(String[] args) {
DataInputStream in = new DataInputStream(System.in);
int f = 0, n = 0;
try {
while (true) {
char x = (char)in.readByte();
if (x=='\n') continue;
if (x=='d' && n==3) {
f += 1;
n = 0;
} else if (x=='c' && n==2) {
n = 3;
} else if (x=='b' && n==1) {
n = 2;
} else if (x=='a') {
n = 1;
} else{
n = 0;
}
}
} catch(Exception e) {
Xterm.println("f = " + f);
}
}
}В данной программе используется метод "readByte", который позволяет вводить символы. При этом символ '\n' также оказывается введенным после того, как пользователь нажимает клавишу "Enter" на клавиатуре. Этот символ необходимо игнорировать, что и реализуется в программе оператором "if (x=='\n') continue".
Не использовавшиеся нами ранее операторы "import java.io.*" и "DataInputStream in = new DataInputStream(System.in)" необходимы для вызова метода "readByte". В остальном программа полностью соответствует проведенному перед ее построением исследованию.
