Лингвистическая нечеткая логика

Логические связки в нечеткой лингвистической логике

Чтобы заложить основу для нечеткой лингвистической логики, необходимо расширить содержание таких логических операций, как отрицание, дизъюнкция, конъюнкция и импликация, применительно к высказываниям, которые имеют не числовые, а лингвистические значения истинности.

При рассмотрении этой проблемы полезно иметь в виду, что если — нечеткое подмножество универсального множества и 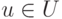, то два следующих утверждения эквивалентны:

1. Степень принадлежности элемента нечеткому множеству есть .
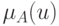2. Значение истинности нечеткого предиката " есть " также равно .

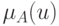Таким образом, вопрос "Что является значением истинности высказывания " есть " И " есть ", если заданы лингвистические значения истинности высказываний " есть " и " есть "?" аналогичен вопросу "Какова степень принадлежности элемента множеству , если заданы степени принадлежности элемента множествам и ?".

В частности, если — точка в , представляющая значение истинности высказывания " есть " (или просто ), где — элемент универсального множества , то значение истинности высказывания " есть не " (или ) определяется выражением

Предположим теперь, что — не точка в , нечеткое подмножество интервала , представленное в виде

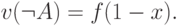
В частности, если значение истинности есть ИСТИННО, т.е. ИСТИННО, то значение истинности ЛОЖНО является значением истинности для высказывания .

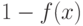Замечание Следует отметить, что если ИСТИННЫЙ , то функция будет интерпретироваться термом НЕ ИСТИННЫЙ, а функция — термом ЛОЖНЫЙ, что в принципе не одно и то же (см. рис. 9.2).

То же самое относится к лингвистическим неопределенностям. Например, если ИСТИННЫЙ , то значение терма ОЧЕНЬ ИСТИННЫЙ равно (см. рис. 9.3).

С другой стороны, если значение истинности высказывания есть , то функция будет выражать значение истинности высказывания "очень ".

Рис. 9.3.

Перейдем к бинарным связкам. Пусть и — лингвистические значения истинности высказываний и соответственно. В случае, когда и — точечные оценки, имеем:

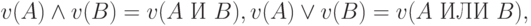
Если и — лингвистические значения истинности, заданные функциями

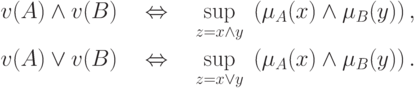
Замечание Важно четко понимать разницу между связкой И (ИЛИ) в терме, например, ИСТИННЫЙ И (ИЛИ) НЕ ИСТИННЫЙ и символом ( ) в высказывании ИСТИННЫЙ ( ) НЕ ИСТИННЫЙ. В первом случае, нас интересует смысл терма ИСТИННЫЙ И (ИЛИ) НЕ ИСТИННЫЙ, и связка И (ИЛИ) определяется отношением

(ИСТИННЫЙ И (ИЛИ) НЕ ИСТИННЫЙ)=

= (ИСТИННЫЙ) ( ) (НЕ ИСТИННЫЙ),

где 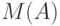— смысл терма . Напротив, в случае терма ИСТИННЫЙ ( ) НЕ ИСТИННЫЙ нас в основном интересует значение истинности высказывания ИСТИННЫЙ НЕ ИСТИННЫЙ, которое получается из равенства

(A И (ИЛИ) B) = .

Значения истинности НЕИЗВЕСТНО и НЕ ОПРЕДЕЛЕНО

Среди возможных значений истинности лингвистической переменной ИСТИННОСТЬ два значения привлекают особое внимание, а именно пустое множество и единичный интервал , которые соответствуют наименьшему и наибольшему элементам (по отношению включения) решетки нечетких подмножеств интервала . Важность именно этих значений истинности обусловлена тем, что их можно интерпретировать как значения истинности НЕ ОПРЕДЕЛЕНО и НЕИЗВЕСТНО соответственно.

Важно четко понимать разницу между и . Когда мы говорим, что степень принадлежности точки множеству есть , мы имеем в виду, что функция принадлежности не определена в точке . Предположим, например, что — множество действительных чисел, а — функция, определенная на множестве целых чисел, причем , если четное, и 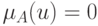, если нечетное. Тогда степень принадлежности числа 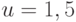множеству есть , а не .

С другой стороны, если бы 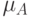была определена на множестве действительных чисел и тогда и только тогда, если — четное число, то степень принадлежности числа 1,5 множеству была бы равна .

Понятие значения истинности НЕИЗВЕСТНО в сочетании с принципом обобщения помогает уяснить некоторые понятия и соотношения обычных двухзначных и трехзначных логик. Эти логики можно рассматривать как вырожденные случаи нечеткой логики, в которой значением истинности НЕИЗВЕСТНО является весь единичный интервал, а не множество .