|
Можно ли, используя функцию Дирихле, построить модель пространства, в котором нет иррациональных чисел, а есть только рациональные числа? Очевидно, нельзя построить плоскость, не используя при этом иррациональные числа, так как плоскость непрерывна. Но пространство обладает бо-льшим числом измерений и может сохранить непрерывность в каком-либо одном из них. |
Элементы теории вероятностей и математической статистики
Часто используется стандартное нормальное распределение или распределение вероятностей нахождения (попадания) случайной величины в интервал (a;b). Для вычисления значений такой функции используется интеграл (таблица значений этого, не берущегося в квадратурах, интеграла):
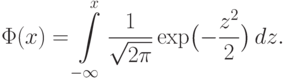
Если известно среднее уклонение случайной величины (средне квадратичное, например), то можно получить представление о величине уклонения ожидаемых фактических значений. Количественную оценку этого дает неравенство П.Л. Чебышева.
Рассмотрим дисперсию с весами
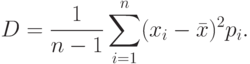
 . Сумма Da - есть сумма вероятностей всех тех значений xi, которые уклоняются от среднего в ту или иную сторону на величину, большую, чем a. По правилу сложения, это будет вероятность того, что величина x получит какое-либо одно из этих значений, то есть вероятность того, что ожидаемое фактическое уклонение окажется больше, чем a. Обозначают эту вероятность так:
. Сумма Da - есть сумма вероятностей всех тех значений xi, которые уклоняются от среднего в ту или иную сторону на величину, большую, чем a. По правилу сложения, это будет вероятность того, что величина x получит какое-либо одно из этих значений, то есть вероятность того, что ожидаемое фактическое уклонение окажется больше, чем a. Обозначают эту вероятность так: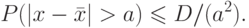
Это неравенство называется неравенством Чебышева. Оно позволяет оценить вероятность уклонений, больших, чем любое заданное число a, если известна дисперсия D (среднеквадратичное отклонение).
Пример. Пусть для заданного ряда чисел имеем: x=100, D=2. Тогда вероятность получения уклонения в измерениях большего, чем 5, будет оцениваться как
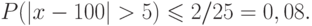
Пусть имеются n взаимно независимых случайных величин 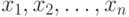 с одними и теми же средним значением b и средним квадратичным уклонением c. Найдем среднее арифметическое этих величин (используя свойства, рассмотренные выше):
с одними и теми же средним значением b и средним квадратичным уклонением c. Найдем среднее арифметическое этих величин (используя свойства, рассмотренные выше):
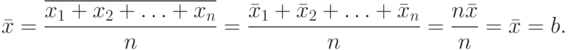
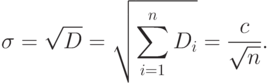
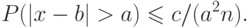
Для любого малого a можно подобрать такое большое n, что правую часть последнего неравенства можно сделать сколь угодно малой, то есть при достаточно большом значении n можно считать имеющим сколь угодно большую (близкую к 1 ) вероятность неравенства вида 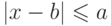 .
.
Этот закон называется законом больших чисел (в его наиболее простой форме). Он был открыт также П.Л. Чебышевым.
Пример. Для предыдущего примера найдем такое n для a=0,1. Получаем неравенство
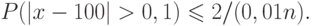
Располагая каким-то распределением величин опытного происхождения, можно исследовать возможность описания этой совокупности каким-либо распределением, рассмотренным выше (если тип распределения неизвестен) или найти (идентифицировать) неизвестный параметр распределения (если тип распределения выяснен), а также эффективность того или иного описания.
Такого рода вопросы формируются обычно в виде статистических гипотез - предположений, обосновываемых или опровергаемых далее.
Пример. Гипотеза первая: данная выборка произведена из нормально распределенной генеральной совокупности. Гипотеза вторая: дисперсии двух рассматриваемых распределений совокупностей равны.
Есть процедуры, позволяющие отвергнуть проверяемую гипотезу как противоречащую имеющимся данным, либо убедиться в том, что гипотеза этим данным не противоречит.
Наиболее часто проверяемой гипотезой является гипотеза о нормальности распределения, то есть о подчиненности ряда нормальному распределению (распределению Гаусса).
Выше, при рассмотрении задачи аппроксимации мы указывали, что экспериментальные данные, по которым отыскивается эмпирическая формула, подвержены ошибкам, например, ошибкам округления. Мы предполагали при этом (правда, неявно), что эти ошибки носят детерминированный характер. Но экспериментальные данные, а также ошибки могут иметь и случайный характер. Такая ситуация встречается чаще. Подход и метод наименьших квадратов, рассмотренные при решении задачи аппроксимации, пригодны и в этих, изменившихся качественно, условиях. Зависимости y=f(x1, x2, ..., xn), определенные для случайных наборов данных и снабженные соответствующими статистическими оценками адекватности, предсказания, как в целом, так и по отдельным факторам xi, i=1,2,...,n, называются регрессионными зависимостями , а сама зависимость - многофакторной регрессионной зависимостью . Возможны и однофакторные зависимости y=f(x). Обычно ищут линейную зависимость вида y=a0+a1x1+a2x2+...+anxn. В других случаях ищут квадратичную многофакторную зависимость. В предыдущем разделе мы рассматривали, как можно методом наименьших квадратов найти однофакторную модель.
