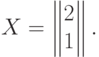|
Можно ли, используя функцию Дирихле, построить модель пространства, в котором нет иррациональных чисел, а есть только рациональные числа? Очевидно, нельзя построить плоскость, не используя при этом иррациональные числа, так как плоскость непрерывна. Но пространство обладает бо-льшим числом измерений и может сохранить непрерывность в каком-либо одном из них. |
Элементы линейной алгебры
Операции сложения, вычитания матриц и умножения на скаляр  удовлетворяют следующим законам:
удовлетворяют следующим законам:
- A+B=B+A ;
- (A+B)+C=A+(B+C) ;
-
 ;
; -
 ;
; -
 ;
; -
 ;
; - A+0=A ;
- A+(-A)=0.
Произведением AB матрицы 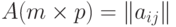 на матрицу
на матрицу 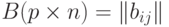 справа (или матрицы B на матрицу A слева) называется матрица
справа (или матрицы B на матрицу A слева) называется матрица 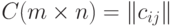 , где каждый ее элемент определяется по формуле
, где каждый ее элемент определяется по формуле

Пример. Найдем произведение матриц вида
![A= \begin{Vmatrix}
2 & 2 & 1 \cr
1 & 5 & -1
\end{Vmatrix}, \quad
B = \begin{Vmatrix}
0 & 1 & 5 \cr
2 & 0 & 2 \cr
5 & 5 & 1
\end{Vmatrix}. \\[4pt]
AB = \begin{Vmatrix}
2\cdot 0 + 2\cdot 2 + 1\cdot 5 & 2\cdot 1+2\cdot 0 +1\cdot5 &
2\cdot 5 +2\cdot 2 + 1\cdot 1 \\[3pt]
1\cdot 0+5\cdot 2 + (-1)\cdot 5& 1\cdot 1+5\cdot 0+(-1)\cdot5&1\cdot
5+5\cdot 2+(-1)\cdot 1
\end{Vmatrix} = \\[3pt]=
\begin{Vmatrix}
9 & 7 & 15 \cr
5 & -4 & 14
\end{Vmatrix} .](/sites/default/files/tex_cache/569bb153bd777d641e2fc891ae5828d7.png)
Операция умножения произвольных матриц A и B и числа  также
удовлетворяет определенным законам.
также
удовлетворяет определенным законам.
Определители матриц обладают определенными свойствами.
Свойство 1. Определитель матрицы не изменится, если в матрице строки и столбцы поменять местами.
Отсюда следует, что все свойства определителя, справедливые для строк, будут справедливы и для столбцов.
Свойство 2. Если в матрице поменять местами две любые строки (два любых столбца), то определитель матрицы (то есть его значение) изменит знак.
Свойство 3. Общий множитель всех элементов некоторой строки (столбца) матрицы можно выносить за знак определителя.
Свойство 4. Если все элементы какой-либо строки (какого-либо столбца) матрицы равны нулю, то определитель равен нулю.
Свойство 5. Если каждый элемент aij, j=1, 2,..., n строки (столбца i=1, 2,..., n ) с номером i (столбца с номером j ) матрицы есть сумма двух чисел, то есть aij=bij+cij, то определитель матрицы можно записать в виде суммы двух определителей: у одного элементами i -ой строки ( j -го столбца) являются числа bij, у другого элементами i -ой строки ( j -го столбца) являются числа cij.
Свойство 6. Определитель матрицы, у которой элементы каких-либо двух строк (столбцов) пропорциональны, равен нулю.
Свойство 7. Если к элементам некоторой строки (столбца) матрицы прибавить соответствующие элементы другой строки (столбца), умноженные на одно и то же число  , то определитель матрицы не изменится.
, то определитель матрицы не изменится.
Свойство 8. Определитель матрицы равен сумме произведений элементов ai1, ai2,..., ain любой строки номера i (элементов a1j, a2j, ..., a_{nj} любого столбца номера j ) матрицы на их алгебраические дополнения Ai1, Aj2, ..., Ain ( Aj1, Aj2, ..., Ajn).
Свойство 9. Сумма произведений элементов какой-либо строки (какого-либо столбца) определителя на алгебраические дополнения другой строки (другого столбца) равна нулю, то есть если 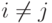 , то ai1Aj1+ai2Aj2+...+ainAjn=0.
, то ai1Aj1+ai2Aj2+...+ainAjn=0.
Правило вычисления определителей. Используя свойство 7, получить из данного определителя другой определитель (имеющий такое же числовое значение), у которого все элементы некоторой строки (некоторого столбца), кроме одного, будут равны нулю, а затем, используя свойство 8, преобразовать последний определитель к определителю порядка на единицу меньше исходного.
Пример. Вычислим определитель A вида (пояснения к цифрам - ниже):
![A = \begin{pmatrix}
1 & -1 & 2 & 1 \cr
-1& 0 & 3 & 3 \cr
1 & -1 & 3 & 1 \cr
2 & -2& 7 & 1
\end{pmatrix}
\mathrel{\mathop{=}\limits^{(1)}}
\begin{pmatrix}
1 & -1 & 2 & 1 \cr
-1& 0 & 3 & 3 \cr
0 & 0 & 1 & 0 \cr
0 & 0& 3 &-1
\end{pmatrix}
\mathrel{\mathop{=}\limits^{(2)}} \\[3pt] =
(-1) (-1)^{1+2}
\begin{pmatrix}
-1 & 3 & 3 \cr
0 & 1 & 0 \cr
0 & 3 & -1
\end{pmatrix} =
\begin{pmatrix}
-1 & 3 & 3 \cr
0 & 1 & 0 \cr
0 & 3 & -1
\end{pmatrix}
\mathrel{\mathop{=}\limits^{(3)}}
1 \cdot \begin{pmatrix}
-1 & 3 \cr
0 & -1 \cr
\end{pmatrix} = \\= 1 - 0 = 1.](/sites/default/files/tex_cache/d3473123f4893882c89cf2811cd7b7e6.png)
Пояснения к цифрам (выполняемым от равенства к равенству эквивалентным преобразованиям): (1) - вычитание из 3-й строки 1-ой строки и вычитание из 4-й строки - 1-й строки, предварительно умноженной на 2; (2) - разложение по элементам 2-го столбца, используя свойство 8; (3) - разложение по элементам 2-й строки.
Обратной к матрице 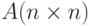 матрицей называется матрица A-1, такая, что
матрицей называется матрица A-1, такая, что  .
.
Теорема.
Для того чтобы у матрицы 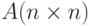 имелась обратная, необходимо и достаточно, чтобы
имелась обратная, необходимо и достаточно, чтобы 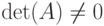 (матрица A была не особой), причем обратную матрицу можно получить по формуле
(матрица A была не особой), причем обратную матрицу можно получить по формуле

Пример. Пусть


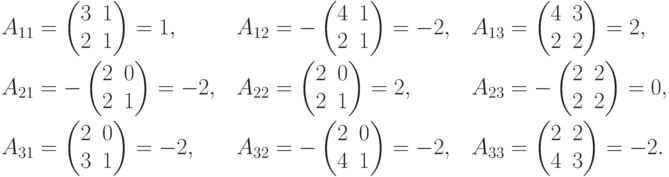
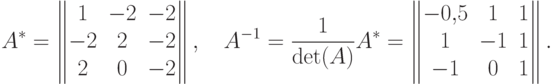
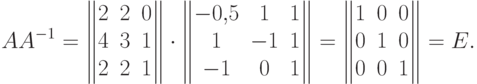
С матрицами связаны очень важные характеристики процессов (систем), описываемых матрицами, - собственные числа и собственные вектора.
Собственное ( характеристическое ) число  квадратной матрицы порядка n - это такое число, для которого существует ненулевое решение матричного уравнения вида
квадратной матрицы порядка n - это такое число, для которого существует ненулевое решение матричного уравнения вида  . Собственным вектором X матрицы A, соответствующим собственному числу
. Собственным вектором X матрицы A, соответствующим собственному числу  , называется это решение X уравнения.
, называется это решение X уравнения.
Для того чтобы найти собственное число, необходимо решить алгебраическое уравнение n -ой степени  .
Это уравнение называется характеристическим уравнением.
.
Это уравнение называется характеристическим уравнением.
Если найдено собственное число  , то соответствующий ему собственный вектор определяется как ненулевое решение матричного уравнения
, то соответствующий ему собственный вектор определяется как ненулевое решение матричного уравнения  .
.
Пример.
Найдем собственные значения и векторы матрицы  . Запишем характеристическое уравнение
. Запишем характеристическое уравнение  , которое будет иметь вид:
, которое будет иметь вид:
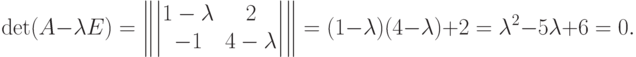
 ,
,  . Найдем собственный вектор, соответствующий числу
. Найдем собственный вектор, соответствующий числу  , то есть ненулевое решение уравнения (A-3E)X=0 или уравнения, записанного в координатной форме:
, то есть ненулевое решение уравнения (A-3E)X=0 или уравнения, записанного в координатной форме:
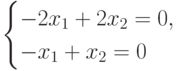
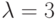 , имеет вид
, имеет вид
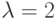 , равен
, равен