Московский государственный университет имени М.В.Ломоносова
Опубликован: 10.09.2007 | Доступ: свободный | Студентов: 4016 / 742 | Оценка: 4.33 / 3.93 | Длительность: 13:22:00
Тема: Математика
Специальности: Математик
Лекция 7:
Единственность главного ступенчатого вида матрицы
Замена базиса линейного пространства
Пусть V - конечномерное линейное пространство над полем K, 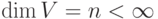 , {v1,...,vn} - базис в V, {v'1,...,v'n} - другой базис в V,
, {v1,...,vn} - базис в V, {v'1,...,v'n} - другой базис в V, 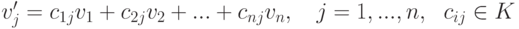 (запись по столбцу!).
(запись по столбцу!).  - матрица перехода от первого базиса ко второму.
- матрица перехода от первого базиса ко второму.
Замечание 9.7.1. Так как умножение в поле K коммутативно, то левое линейное пространство K V можно рассматривать и как правое линейное пространство V_K, полагая  для всех
для всех 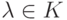 ,
, 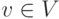 . Тогда определение матрицы перехода может быть записано в матричном виде как (v'1,...,v'n)=(v1,...,vn)C.
Ограничиваясь левыми линейными пространствами, мы можем использовать эквивалентную форму записи:
. Тогда определение матрицы перехода может быть записано в матричном виде как (v'1,...,v'n)=(v1,...,vn)C.
Ограничиваясь левыми линейными пространствами, мы можем использовать эквивалентную форму записи:
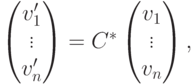
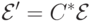

 ,
, 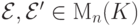 и
и  означает равенство квадратных
означает равенство квадратных  -матриц.
-матриц.