Определители и их свойства
Вывод следствий из свойств 1-4
Нам удобно следующие далее свойства выводить из "базовых" свойств 1 4.
Свойство 5. Если Ai=(0,...,0), то |A|=0.
Так как 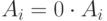 , то
, то 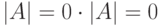 .
.
Свойство 6. Пусть K= R (или K - любое поле).Если 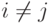 и Ai=Aj, то |A|=0.
и Ai=Aj, то |A|=0.
- Сначала приведем доказательство для случая K= R (или для поля K,
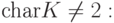 из 2a=0 следует a=0 ). Действительно, переставляя строки Ai и Aj, получаем |A|=-|A|, 2|A|=0, и поэтому |A|=0.
из 2a=0 следует a=0 ). Действительно, переставляя строки Ai и Aj, получаем |A|=-|A|, 2|A|=0, и поэтому |A|=0. - Приведем общее доказательство в случае любого поля K при
 . Пусть i<j. Для каждой подстановки
. Пусть i<j. Для каждой подстановки  , участвующей в выражении определителярассмотрим подстановку
, участвующей в выражении определителярассмотрим подстановку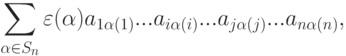 полученную из
полученную из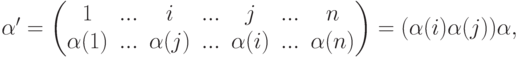
 переменой местами чисел
переменой местами чисел  и
и  в нижней строке канонической записи. Ясно, что
в нижней строке канонической записи. Ясно, что  . Так как Ai=Aj, то aik=ajk для k=1,...,n,
. Так как Ai=Aj, то aik=ajk для k=1,...,n,  ,
,  . Поэтому
. Поэтому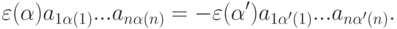
Если 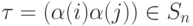 , то
, то 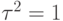 и отношение
и отношение  для
для 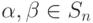 , где
, где  означает, что
означает, что  или
или  , является отношением эквивалентности. Действительно,
, является отношением эквивалентности. Действительно,
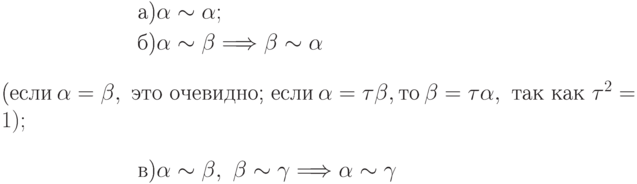
(имеем четыре случая
-
 ,
,  , поэтому
, поэтому 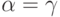 ;
; -
 ,
,  , поэтому
, поэтому 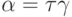 ;
; -
 ,
, 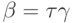 , поэтому
, поэтому 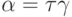 ;
; -
 ,
, 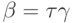 , поэтому
, поэтому 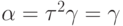 ; и поэтому
; и поэтому 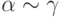 ).
).
Таким образом, разбиение на классы эквивалентных элементов приводит к разбиению на непересекающиеся классы 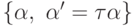 . При
. При  сумма n! четного числа слагаемых разбивается на суммы пар слагаемых по подстановке
сумма n! четного числа слагаемых разбивается на суммы пар слагаемых по подстановке  и по подстановке
и по подстановке 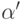 , равные нулю, поскольку эти два слагаемые отличаются знаком.
, равные нулю, поскольку эти два слагаемые отличаются знаком.
Свойство 7. Если от квадратной матрицы A переходим к матрице A' с помощью элементарного преобразования 1-го типа A'i=Ai+cAj, 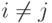 ,
,  , то |A'|=|A|.
, то |A'|=|A|.
Действительно, разлагая определитель |A'| в сумму двух определителей (по i -й строке), мы получаем |A| и нулевой определитель, в котором после вынесения из i -й строки числа c имеем две одинаковые строки ( Aj на месте i -й строки и Aj на своем j -м месте).
Линейная комбинация строк в линейном пространстве строк K^n
Если
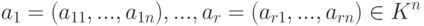
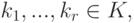
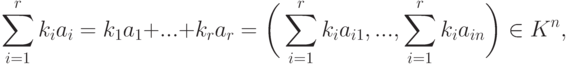

Свойство 8. Если найдется строка Ai, являющаяся линейной комбинацией остальных строк квадратной матрицы A, то |A|=0.
Действительно, если
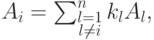
Определение 6.5.1. Если A=(aij) - квадратная  -матрица, то
-матрица, то  -матрица A*=(bij), bij=aji, называется матрицей, полученной транспонированием из матрицы A (т. е. симметрией относительно диагонали).
-матрица A*=(bij), bij=aji, называется матрицей, полученной транспонированием из матрицы A (т. е. симметрией относительно диагонали).
Теорема 6.5.2. |A*|=|A| (определитель квадратной матрицы не меняется при транспонировании).
Доказательство. Каждый член 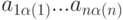 определителя
определителя
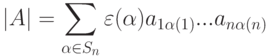
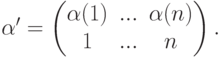
 , то в итоге мы имеем |A*|=|A|.
, то в итоге мы имеем |A*|=|A|.Следствие 6.5.3. Свойства 1-8 выполняются и для столбцов определителя |A| квадратной  -матрицы A.
-матрицы A.
Действительно, при переходе от матрицы A к транспонированной матрице A* строки превращаются в столбцы, а столбцы - в строки. Преобразования строк транспонированной матрицы A* соответствуют преобразованиям столбцов матрицы A.
