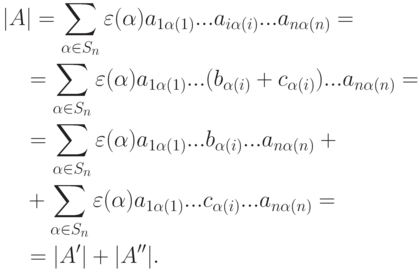НОУ ИНТУИТ | Алгебра матриц и линейные пространства. Лекция 1: Определители и их свойства

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Твой путь к знаниям!

Московский государственный университет имени М.В.Ломоносова

Опубликован: 10.09.2007 | Доступ: свободный | Студентов: 3973 / 713 | Оценка: 4.33 / 3.93 | Длительность: 13:22:00

Тема: Математика

Специальности: Математик

Теги: beta, TE, алгебраическим дополнением, вычисления, геометрия, законы дистрибутивности, игры, линейная оболочка строк, матрица перехода, моноид, определитель матрицы, расширенная матрица, система линейных уравнений определенная, собственный вектор, теория, элементы

|

Вам нравится? Нравится 62 студентам

| Поделиться |

Поддержать курс

| Скачать электронную книгу

Свойства определителя. Базовые свойства 1-4

Свойство 1. Если

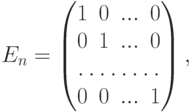
$E_n= \begin{pmatrix} 1 & 0 & ... & 0\\ 0 & 1 & ... & 0\\ \hdotsfor{4}\\ 0 & 0 & ... & 1 \end{pmatrix},$

то |E|=1.

Доказательство. следует из следующего утверждения.

Лемма 6.3.1.

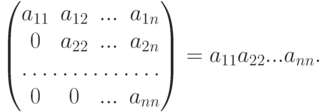
$\begin{pmatrix} a_{11} & a_{12} & ... & a_{1n}\\ 0 & a_{22} & ... & a_{2n}\\ \hdotsfor{4}\\ 0 & 0 & ... & a_{nn} \end{pmatrix} = a_{11}a_{22}... a_{nn}.$

Доказательство. Следует рассмотреть только те произведения, входящие в определитель, которые из первого столбца содержат сомножителем a₁₁ (остальные равны нулю). Вхождение сомножителя a₁₁ занимает первую строку и первый столбец. Из второго столбца (при уже занятой первой строчке) остается включить в произведение a₂₂ (остальные произведения равны нулю). Повторяя это рассуждение, приходим к произведению a₁₁a₂₂... a_nn (остальные из n! произведений все равны нулю).

Так как подстановка

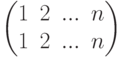
$\begin{pmatrix} 1 & 2 & ... & n\\ 1 & 2 & ... & n \end{pmatrix}$

четная, то это произведение входит со знаком +.

Следствие 6.3.2.

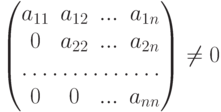
$\begin{pmatrix} a_{11} & a_{12} & ... & a_{1n}\\ 0 & a_{22} & ... & a_{2n}\\ \hdotsfor{4}\\ 0 & 0 & ... & a_{nn} \end{pmatrix} \neq 0$

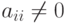тогда и только тогда, когда все $a_{ii}\neq 0$ , $1 \leq i \leq n$ .

Задача 6.3.3. Чему равен определитель

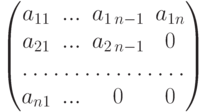
$\begin{pmatrix} a_{11} & ... & a_{1\,n-1} & a_{1n}\\ a_{21} & ... & a_{2\,n-1} & 0\\ \hdotsfor{4}\\ a_{n1} & ... & 0 & 0 \end{pmatrix}$

(т. е. чему равен определитель, в котором все элементы ниже побочной диагонали равны нулю)?

Свойство 2. При перестановке двух строк A_i и A_j, 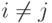$i\neq j$ , матрицы A определитель меняет знак ( |A'|=-|A|, где A' - матрица, полученная из матрицы A перестановкой двух строк).

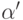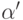Доказательство. Произведение $\varepsilon(\alpha)a_{1\alpha(1)}... a_{n\alpha(n)}$ из |A| входит также в |A'|, при этом новая подстановка индексов $\alpha'$ отличается от $\alpha$ одной транспозицией i и j в верхней строке (номера строк), таким образом, в $\alpha'$ имеем

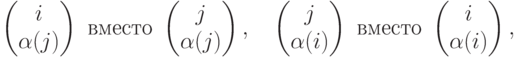
$\begin{pmatrix} i\\ \alpha(j) \end{pmatrix} \text{ вместо } \begin{pmatrix} j\\ \alpha(j) \end{pmatrix},\quad \begin{pmatrix} j\\ \alpha(i) \end{pmatrix} \text{ вместо } \begin{pmatrix} i\\ \alpha(i) \end{pmatrix},$

поэтому $\varepsilon(\alpha')=-\varepsilon(\alpha)$ .

Свойство 3. Если A'_i = cA_i (т. е. i -я строка матрицы A умножена на число c ), то |A'|=c|A|.

Доказательство. В каждое произведение, входящее в |A'|, из i -й строки входит только один сомножитель $ca_{i\alpha(i)}$ , таким образом, |A'|=c|A|.

Упражнение 6.3.4. Если 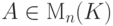$A\in\mM_n(K)$ , то |c A| = cⁿ |A|.

Свойство 4. Если A_i=(a_i1,...,a_in)=(b₁,...,b_n)+(c₁,...,c_n)=B+C (т. е. i -я строка в матрице A представлена суммой двух строк), то |A| равен сумме двух определителей |A'|+|A''| матриц A' и A'', в которых вместо i -й строки A_i в A стоят соответственно строки B и C.

Доказательство. В каждое произведение

$\varepsilon(\alpha)a_{1\alpha(1)}... a_{n\alpha(n)}$

входит из i -й строки A_i только один сомножитель

$a_{i\alpha(i)}=b_{\alpha(i)}+c_{\alpha(i)}.$

Таким образом,

$\begin{align*} & |A| = \sum_{\alpha\in S_n} \varepsilon(\alpha) a_{1\alpha(1)}... a_{i\alpha(i)}... a_{n\alpha(n)} ={} \\ & \quad {}= \sum_{\alpha\in S_n} \varepsilon(\alpha) a_{1\alpha(1)}... (b_{\alpha(i)}+c_{\alpha(i)}) ... a_{n\alpha(n)} ={} \\ & \quad {}= \sum_{\alpha\in S_n} \varepsilon(\alpha) a_{1\alpha(1)}... b_{\alpha(i)} ... a_{n\alpha(n)} +{} \\ & \quad {}+ \sum_{\alpha\in S_n} \varepsilon(\alpha) a_{1\alpha(1)}... c_{\alpha(i)} ... a_{n\alpha(n)} ={} \\ & \quad {}= |A'| + |A''|. \end{align*}$

Дальше >>

Авторизоваться

Алгебра матриц и линейные пространства

Определители и их свойства

Свойства определителя. Базовые свойства 1-4

Вопросы и ответы