НОУ ИНТУИТ | Практикум по компьютерной геометрии. Лекция 1: Первое знакомство с пакетом Mathematica

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

Опубликован: 27.12.2010 | Доступ: свободный | Студентов: 1031 / 279 | Оценка: 5.00 / 5.00 | Длительность: 18:38:00

ISBN: 978-5-9556-0117-5

Темы: Математика, САПР

Специальности: Математик

Теги: алгебра, анализ, вычисления, геометрия, программное обеспечение

|

Вам нравится? Нравится 14 студентам

| Поделиться |

Поддержать курс

| Скачать электронную книгу

Упражнения

Задачи взяты из книги А. С. Мищенко, Ю. П. Соловьева, А. Т. Фоменко, "Сборник задач по дифференциальной геометрии и топологии" [5].

(2.1) Точка равномерно движется по прямой 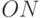, равномерно вращающейся вокруг точки . Составить уравнение траектории точки (спираль Архимеда).

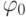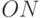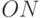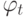Решение. Пусть - начало координат. Если $\varphi_0$ - начальный угол между прямой и положительным направлением оси абсцисс, а $\omega$ - угловая скорость вращения прямой вокруг , то в момент времени угол $\varphi_t$ между 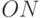и осью абсцисс изменяется линейно и записывается в виде

$\tt In[209]:= $\varphi$ [t\_]:=$\varphi$ 0+ $\omega$ t$

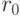Если начальное расстояние от до равно r_0 , а точка движется по 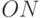со скоростью , то в момент времени расстояние r[t] между и равно

$\tt In[210]:= r[t\_]:=r0+vt;$

Таким образом, координаты точки в момент времени равны

$\tt In[211]:= $\gamma$[t\_]:=r[t] \{Cos[$\varphi$[t]], Sin[$\varphi$[t]]\} \\ \\ In[212]:= $\gamma$[t] \\ \\ Out[212]=\{(r0+tv)Cos[$\varphi$0+t$\omega$], (r0+tv)Sin[$\varphi$0+t$\omega$]\}$

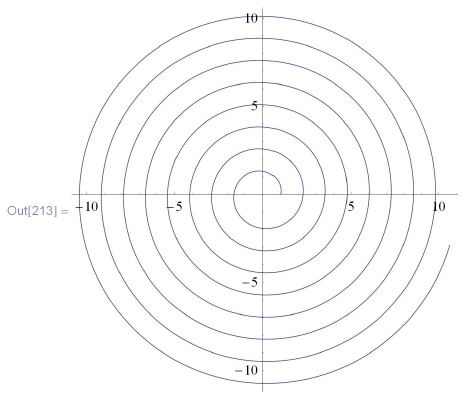
Изобразим траекторию, фиксировав некоторые значения параметров:

$\tt In[213]:=ParametricPlot[$\gamma$[t] /. \{$\varphi$0 $\to$ 0, r0 $\to$ 1, $\omega$ $\to$ 5, v $\to$ 1\}, \\ \phantom{In[213]:=P}\{t, 0, 10\}]$

$\tt In[214]: Clear[$\varphi$, $\gamma$, r]$

(2.19) Под каким углом пересекаются кривые x^2=4y и $y=\frac{8}{x^2+4}$ ?

Решение. Найдем точки пересечения кривых:

$\tt In[215]:=res=Solve$\left[\left\{x^{2}==4y, y== \frac{8}{x^2+4)\right\},\{x,y\}\right]$ \\ \\ Out[215]=$\left\{\left\{y \to -2, x \to -2i \sqrt{2}\right\}\right.$, \\ \\ \phantom{Out[215]= }$\left.\left\{y \to -2, x \to 2i \sqrt{2}\right\}, \{y \to 1, x \to -2\}, \{y\to 1, x\to 2\} \right\}$$

Так как кривые вещественные, подходят лишь третье и четвертое решения. Так как кривые инвариантны при замене на , углы пересечения в обеих точках одинаковы, поэтому достаточно вычислить угол лишь, скажем, для четвертого решения. Заметим, что обе кривые являются графиками функций параметра , поэтому они могут быть параметризованы . Имеем (функция $\text{\tt Norm[v]}$ , которую мы используем ниже, равна евклидовой длине вектора )

$\text{In[216]:=}\gamma 1[x\_]:=\left\{x, \frac{x^2}{4}\right\}; \gamma 2[x\_]:=\left\{x, \frac{8}{x^2+4}\right\};\\ \phantom{\text{In[216]:=}}v1:=\gamma 1'[x]\text{ /. res}[\![4]\!]; v2:=\gamma 2'[x]\text{ /. res}[\![4]\!];\\ \phantom{\text{In[216]:=}}\varphi=\text{ArcCos} \left[\frac{v1.v2}{\text{Norm}[v1]\text{Norm}[v2]}\right] \\ \\ \text{Out[218]=ArcCos}\left[\frac{1}{\sqrt{10}}\right]$

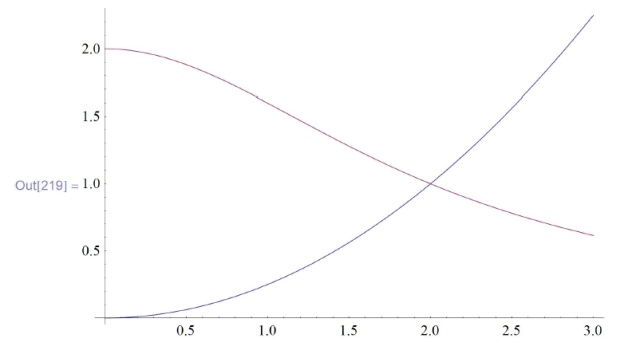
Изобразим эти кривые:

$\text{In[219]:=Plot}\left[\left\{\frac{x^2}{4}, \frac{8}{x^2+4}\right\}, \{x,0,3\}\right]$

$\tt In[220]:=Clear[$\gamma$1, $\gamma$2, v1, v2, res, $\varphi$]$

(2.22) Вокруг оси 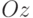вращается окружность x = a + b cos[v], z =b sin[v] (0 < b < a) . Составить уравнение поверхности вращения.

Решение. Если точку с координатами {a+b cos[v], 0, b sin[v]} повернуть на угол $\varphi$ вокруг оси 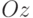, то у полученной точки будут координаты

$\tt In[221]:=r[$\varphi$\_, v\_] := \{(a+b Cos[v])Cos[$\varphi$], (a+bCos[v])Sin[$\varphi$], \\ \phantom{In[221]:=r[$\varphi$}b Sin[v]\};$

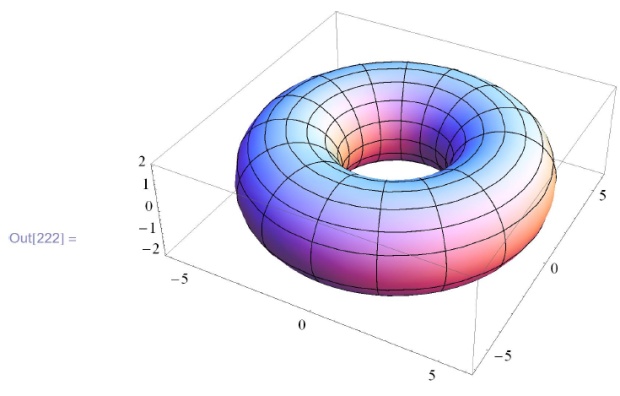
Нарисуем эту поверхность (являющуюся, очевидно, тором) при следующих значениях параметров: 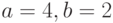a = 4, b = 2 при изменении $\varphi$ и в пределах от 0 до $2 \pi$ .

$\tt In[222]:=ParametricPlot3D[r[$\varphi$, v]/. \{a $\to$ 4, b $\to$ 2\}, \{$\varphi$, 0, 2$\pi$ \}, \\ \phantom{In[222]:=P}\{v, 0, 2 $\pi$\}]$

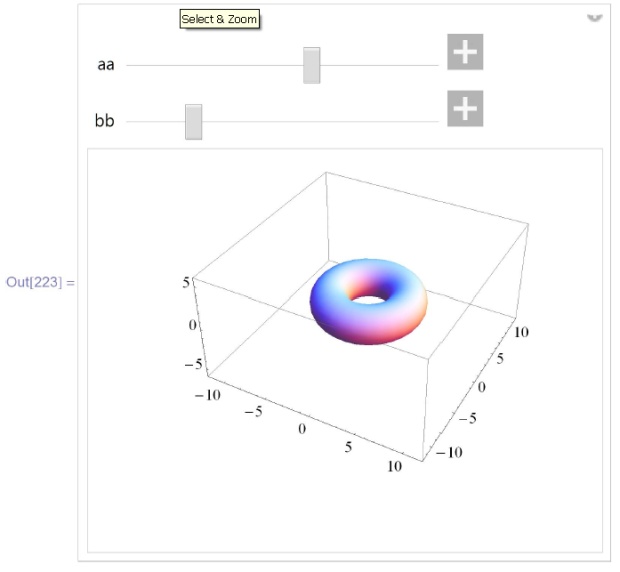
Изобразим зависимость тора от параметров (здесь 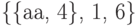$\text{\pp \{\{aa, 4\}, 1, 6\}}$ означает, что параметр 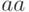может меняться в пределах между 1 и 6, причем начальное его значение равно 4; аналогично для параметра ):

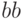$\tt In[223]:= \\ \\ \phantom{In}Module[\{r,a,b\}, \\ \phantom{InM}r[$\varphi$\_, v\_] := \{(a+bCos[v])Cos[$\varphi$], (a+bCos[v])Sin[$\varphi$], \\ \phantom{InMod}bSin[v]\}; \\ \phantom{InM}Manipulate[ParametricPlot3D[r[$\varphi$, v] /. \{a$\to$aa, b$\to$bb\}, \\ \phantom{InMod}\{$\varphi$, 0, 2$\pi$\}, \{v, 0, 2$\pi$\}, Mesh$\to$None, PlotPoints$\to$30, \\ \phantom{InMod}PlotRange$\to$\{\{-12,12\}, \{-12, 12\}, \{-6,6\}\}, ImageSize$\to$300], \\ \phantom{InMo}\{\{aa, 4\}1,6\}, \{\{bb,2\},1,6\}] \\ \phantom{In}]$

$\tt In[224]:=Clear[r]$

Дальше >>

Авторизоваться

Практикум по компьютерной геометрии

Первое знакомство с пакетом Mathematica

Упражнения

Вопросы и ответы