Опубликован: 27.12.2010 | Доступ: свободный | Студентов: 1031 / 279 | Оценка: 5.00 / 5.00 | Длительность: 18:38:00
ISBN: 978-5-9556-0117-5
Темы: Математика, САПР
Специальности: Математик
Теги:
Лекция 1:
Первое знакомство с пакетом Mathematica
Визуализация зависимости от параметра
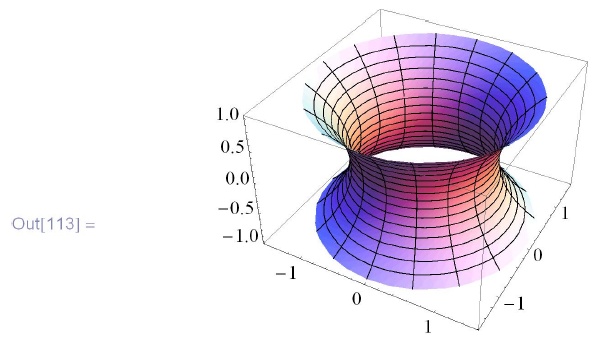
Катеноид (минимальная поверхность вращения):
![\tt
In[113]:=ParametricPlot3D[\{Cosh[u] Cos[v], Cosh[u] Sin[v], u\}, \\
\phantom{In[113]:=P}\{u,-1,1\}, \{v,0,2\pi\}]](/sites/default/files/tex_cache/c06afff2198de294be963a6a9d1c309b.png)
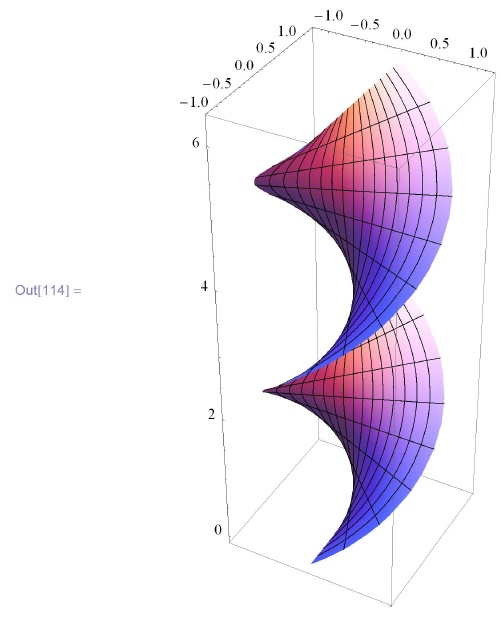
Геликоид (минимальная линейчатая поверхность):
![\tt
In[114]:=ParametricPlot3D[\{Sinh[u] Sin[v], -Sinh[u] Cos[v], v\}, \\
\phantom{In[114]:=P}\!\{u,-1,1\}, \{v, 0, 2\pi\}]](/sites/default/files/tex_cache/8127f6e7d8a8ddcb6baedf7267d030b7.png)
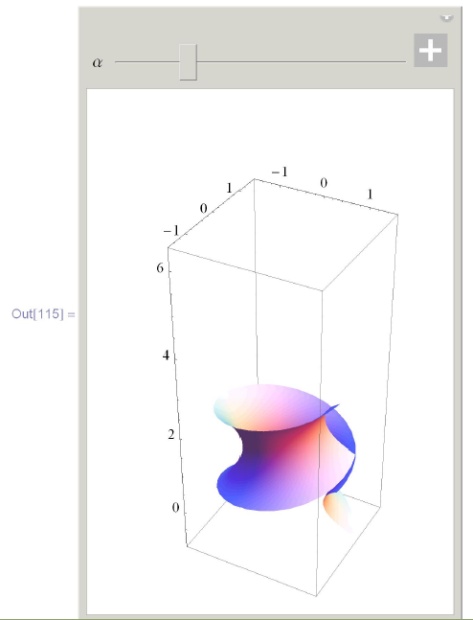
Изгибание катеноида в геликоид (здесь  описывает отрезки изменения координат
описывает отрезки изменения координат 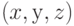 точек поверхности;
точек поверхности;  - координатная сетка на поверхности, в данном случае
- координатная сетка на поверхности, в данном случае  означает, что сетка отсутствует;
означает, что сетка отсутствует;  - количество точек на каждой координатной кривой: чем больше точек, тем более гладко выглядит поверхность, хотя прорисовка замедляется;
- количество точек на каждой координатной кривой: чем больше точек, тем более гладко выглядит поверхность, хотя прорисовка замедляется;  - параметр изгибания).
- параметр изгибания).
![\tt
In[115]:= \\ \\
\phantom{In}Manipulate[ \\
\phantom{\phantom{In}M}ParametricPlot3D[Cos[$\alpha$] \{Cosh[u] Cos[v], Cosh[u] Sin[v], u\}+ \\
\phantom{\phantom{\phantom{In}M}Pa}Sin[$\alpha$] \{Sinh[u] Sin[v], - Sinh[u] Cos[v], v\}, \{u, -1, 1\}, \\
\phantom{\phantom{\phantom{In}M}P}\{v, 0, 2$\pi$\}, \\
\phantom{\phantom{\phantom{In}M}P}PlotRange $\to$ \{\{-1.6, 1.6\}, \{-1.6, 1.6\}, \{-1, 6.5\}\}, Mesh $\to$ None, \\
\phantom{\phantom{\phantom{In}M}P}PlotPoints $\to$ 30, ImageSize $\to$ 200], \\
\phantom{\phantom{In}M}\{$\alpha$, 0, $\frac{\pi}{2}$\}]](/sites/default/files/tex_cache/4a7b47924adb620f6aed38e985c299ac.png)
Алгебра и анализ
Дифференцирование и интегрирование
![\tt
In[116]:=f[x\_] := $x^2$\tt\;Sin[x] \\
\phantom{In[116]:=}D[f[x],x] \\
\phantom{In[116]:=}f'[x] \\
\phantom{In[116]:=}Integrate[f[x],x] \\
\phantom{In[116]:=}$\int$ f[x] dx \\
\phantom{In[116]:=}Integrate[$x^2$, \{x, a, b\}] \\
\phantom{In[116]:=}$\int_a^b x^2$ dx \\ \\
Out[117]=$x^2$ Cos[x]+2x Sin [x] \\ \\
Out[118]=$x^2$ Cos[x]+2x Sin [x] \\ \\
Out[119]=-(-2+$x^2$) Cos[x] + 2x Sin[x] \\ \\
Out[120]=-(-2+$x^2$) Cos[x] + 2x Sin[x] \\ \\
Out[121]=$-\frac{a^3}{3} + \frac{b^3}{3}$ \\ \\
Out[122]=$-\frac{a^3}{3} + \frac{b^3}{3}$](/sites/default/files/tex_cache/fe0367e00ef2efffb92c8bdba1228ce6.png)
Численное интегрирование
![\tt
In[123]:=NIntegrate [Sin[Cos[x]], \{x,1,2\}] \\
\phantom{In[123]:=}$\int_1^2$\tt Sin[Cos[x]] dx \\
\phantom{In[123]:=}N[$\int_1^2$ Sin[Cos[x]] dx] \\ \\
Out[123]=0.652202 \\ \\
Out[124]=$\int_1^2$ Sin[Cos[x]] dx \\ \\
Out[125]=0.0652202](/sites/default/files/tex_cache/0d3c6ab8f0051a111468c32a0a8799a3.png)