Первое знакомство с пакетом Mathematica
Замена фрагментов выражения expr по правилам rules (ReplaceAll): expr /. Rules
Значок 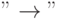 получается последовательным набором - и > или с использованием палетки
получается последовательным набором - и > или с использованием палетки  .
.
![\tt
In[126]:= \{Cos[x], x\^\,\!2 + z\^\,\!3, у, z} /. x $\to$ b\} \\ \\
\tt Out[126]= \{Cos[b], $b^2 + z^3, y, z$\} \\ \\
In[127]:= \{Cos[x], x\^\,\!2 + x\^\,\!3, у, z\} /. Cos $\to$ Sin \\ \\
\tt Out[127]= \{Sin[x], $x^2 + z^3, y, z$\} \\ \\
In[128]:= \{Cos[x], x\^\,\!2 + z\^\,\!3, y, z\} /. z $\to$ \{a, b\} \\ \\
\tt Out[l28]= \{Cos[x], $\{a^3+x^2, b^3+x^2\}, y, \{a, b\}$\} \\ \\
ln[129]:= \{Cos[x], х\^\,\!2 + z\^\,\!3, у, z\} /. \{x $\to$ a, у $\to$ b\} \\ \\
\tt Out[129]= \{Cos[a], $a^2 + z^3, b, z$\} \\ \\
In[130]:= \{Cos[x], х\^\,\!2 + z\^\,\!3, у, z\} /. \{\{x $\to$ a\} , \{y $\to$ b\}\} \\ \\
\tt Out[130]= \{\{Cos[a], $a^2 + z^3, y, z$\}, \{cos[x], $x^2 + z^3, b, z$\}\} \\ \\
In[131]:= \{Cos[x], x\^\,\!2 + z\^\,\!3, y, z\} /. \{x $\to$ a, a $\to$ b\} \\ \\
\tt 0ut[131]= \{Cos[a], $a^2 + z^3, y, z$\} \\ \\
In[132]:= \{Cos[x], x\^\,\!2 + z\^\,\!3, y, z\} /. x $\to$ a /. a $\to$ b \\ \\
\tt Out[132]= \{Cos[b], $b^2 + z^3, y, z$\}](/sites/default/files/tex_cache/df5c2726c3e7574afb56934f79feb9df.png)
Значок 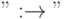 получается последовательным набором
получается последовательным набором  и
и  или с использованием палетки
или с использованием палетки  . В отличие от
. В отличие от  , которое сначала вычисляет
, которое сначала вычисляет  , а потом заменяет на результат вычислений все вхождения
, а потом заменяет на результат вычислений все вхождения  , правило
, правило  вычисляет
вычисляет  отдельно для каждого вхождения
отдельно для каждого вхождения  :
:
![\tt
In[133]:={x, х, х} /. x $\to$ Random[] \\
\phantom{In[133]:=}{х, х, х} /. х :$\to$ Random[] \\ \\
Out[133]={0.209741, 0.209741, 0.209741} \\ \\
Out[134]={0.0161126, 0.191289, 0.729859}](/sites/default/files/tex_cache/a8f3ff374395a5498e6fa9a5a6592be0.png)
Равенства и неравенства
Значки  ,
,  и
и  получаются последовательным набором
получаются последовательным набором 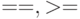 и
и  соответственно или с использованием палетки
соответственно или с использованием палетки  .
.
![\tt
In[135]:=x == 2 \\
\phantom{In[135]:=}x > 3 \\
\phantom{In[135]:=}x $\geq$ 3 \\
\phantom{In[135]:=}(x $\geq$ 3 \&\& x $\leq$ 6)||(x == 8) \\ \\
Out[135]=x == 2 \\ \\
Out[136]=x > 3 \\ \\
Out[137]=x $\geq$ 3 \\ \\
Out[138]=[x $\geq$ 3 \&\& x $\leq$ 6) || x == 8](/sites/default/files/tex_cache/a110f842ea3b5a5ae79331069ac08138.png)
Решение уравнений и неравенств
![\tt
In[139]:= res=Solve[ax^2+bx+c= =0, x]}\\ \\
Out[139]=\{\{x \to \frac{-b-\sqrt{b^2-4ac}}{2a}\}, \{x \to \frac{-b+\sqrt{b^2-4ac}}{2a}\}\\ \\
In[140]:= x/.res[\![1]\!]}\\ \\
Out[140]=\frac{-b-\sqrt{b^2-4ac}}{2a}\\ \\
In[141]:= Solve[\{x^2-y-4= =0, y+3x= =2\}, \{x,y\}]}\\ \\
Out[141]=\{\{y \to \frac12 (13-3 \sqrt{33}), x \to \frac12 (-3+\sqrt{33})\},\\
\phantom{Out[141]=\{}\{y \to \frac12 (13+3 \sqrt{33}, x \to \frac12 (-3- \sqrt{33})\}\} \\ \\
In[142]:= Reduce[ax^2+bx+c==0,x]}\\ \\
Out[142]=\left( a \ne 0 \& \& \left( x==\frac{-b-\sqrt{b^2-4ac}}{2a}\|x==\frac{-b+\sqrt{b^2-4ac}}{2a} \right) \right)\|\\
\phantom{Out[142]=\left(}(a==0 \& \& b \ne 0 \& \& x==-\fraccb)\|(c==0 \& \& b==0 \& \& a==0) \\ \\
In[143]:= Reduce[-1 \le x+y \le 1 \& \& x^2+y^2==2, \{x,y\}]}\\ \\
Out[143]=(\frac12 (-1-\sqrt3) \le x \le \frac12 (1- \sqrt3) \& \& y==\sqrt{2-x^2})\|\\
\phantom{Out[143]=(}(\frac12 (-1+\sqrt3) \le x \le \frac12 (1+\sqrt3) \&\& y==-\sqrt{2-x^2}) \\ \\
In[144]:= Clear[res]}\\](/sites/default/files/tex_cache/903f4799589a29e4be665541fe866326.png)
Решение дифференциальных уравнений
![\tt
In[145]:=res=DSolve[x''[t]-x'[t]==2, x[t],t] \\ \\
Out[145]=\{\{x[t] $\to$ -2t + $e^t$ C[1]+C[2]\}\} \\ \\
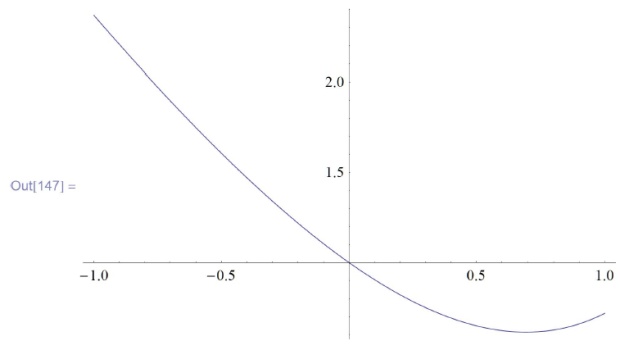
In[146]:=f[t\_]=x[t]/.res[[1]] /. \{C[1] $\to$ 1, C[2] $\to$ 0\} \\ \\
Out[146]=$e^t$ - 2t \\ \\
In[147]:=Plot[f[t], {t, -1,1}]](/sites/default/files/tex_cache/063ff2788bc4a8f21fb2aad159d02a17.png)
![\tt In[148]:= Clear[f, res]](/sites/default/files/tex_cache/de1535b9b332ef354962601b2e1e633a.png)
Численное решение дифференциальных уравнений
Кроме самого уравнения, нужно задать начальные условия и область изменения переменной:
![\tt
In[149]:=\\
\phantom{In}res=NDSolve[{x''[t]-Sin[x'[t]]==2, x[0]==1, x'[0]==2}, \\
\phantom{\phantom{In}re}x,\{t,0,1\}] \\ \\
Out[149]=\{\{x $\to$ InterpolatingFunction[\{\{0.,1.\}\}, <>]\}\} \\ \\
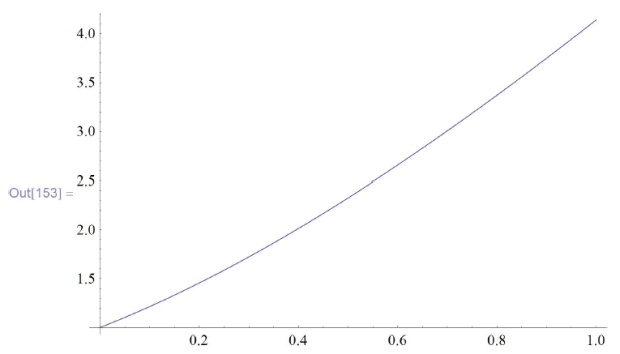
In[150]:=f=x /. res[\![1]\!] \\ \\
Out[150]=InterpolatingFunction[\{\{0.,1.\}\}, <>] \\ \\
In[151]:=f[0] \\
\phantom{In[151]:=}f'[0] \\ \\
Out[151]=1. \\ \\
Out[152]=2. \\ \\
In[153]:= Plot[f[s],{s,0,1}]](/sites/default/files/tex_cache/13316b480a2ebcb65c32ef0e240cb719.png)
![\tt
n[154]:= Clear[res,f]](/sites/default/files/tex_cache/7cf7fce906cac82891b1277a55532cea.png)
Преобразование выражений, упрощение
![\tt
In[155]:=$(x+y)^5$ \\ \\
Out[155]=$(x+y)^5$ \\ \\
In[156]:=$(x+y)^5$ //Expand \\ \\
Out[156]=$x^5+5x^4y+10x^3y^2+10x^2y^3+5xy^4+y^5$ \\ \\
In[157]:=$\frac1x + \frac{x-2}{x^2+3}$ \\ \\
Out[157]=$\frac1x +\frac{-2+x}{3+x^2}$ \\ \\
In[158]:=$\frac1x + \frac{x-2}{x^2+3}$ //Together \\ \\
Out[158]=$\frac{3-2x+2x^2}{x(3+x^2)}$ \\ \\
In[159]:=$8x^2-6x^2+x^4-2x^2y+x^3y-8y^3+6xy^3-x^2y^3+2y^4-xy^4$ // Factor \\ \\
Out[159]=$(-2+x)(-4+x+y)(x^2-y^3)$ \\ \\
In[160]:=Sin$[x]^2$+Cos$[x]^2$ \\ \\
Out[160]=Cos$[x]^2$+Sin$[x]^2$ \\ \\
In[161]:=Sin$[x]^2$+Cos$[x]^2$ //Simplify \\ \\
Out[161]=1](/sites/default/files/tex_cache/98fa293ff75ee9cf8ed55d2fab077183.png)
Программирование
Булевы операции
-
![\text{\tt And[]}](/sites/default/files/tex_cache/50b7538a9f9644996bb14dab99788eb0.png) , или
, или 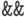 , или
, или  (набрать
(набрать 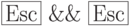 ),
), -
![\text{\tt Or[]}](/sites/default/files/tex_cache/3dae6d028f537a7ae6e34c40d3416cdd.png) , или
, или 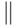 , или
, или  (набрать
(набрать  ),
), -
![\text{\tt Not[]}](/sites/default/files/tex_cache/02f9f7f07cbb0c1a34bf1e3015290dcf.png) , или
, или 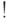 , или
, или 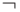 (набрать
(набрать  ),
), -
![\text{\tt Equal[]}](/sites/default/files/tex_cache/78d9fb10f729f6e4fbd4869996a1106c.png) или
или  ,
, -
![Unequal[ ]](/sites/default/files/tex_cache/c50e78affbaf23c59bbfb5d07f805cc2.png) или
или 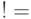 ,
, 
-
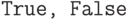 ,
, 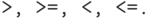
![\tt
In[162]:= 2 > 1 \&\& $\pi$ > 3 \\ \\
Out[162]=True \\ \\
In[163]:= 1 > 2 \|\; $\pi$ > 3 \\ \\
Out[163]=True \\ \\
In[164]:= !x > 1 \\ \\
Out[164]=x $\le$ 1 \\ \\
In[164]:= 2+2==4 \\ \\
Out[165]=True \\ \\
In[166]:= 1 $\ne$ 2 \\ \\
Out[166]=True](/sites/default/files/tex_cache/c3aab349a315475a7f7ddff7ce41d258.png)
Условные операторы
Оператор If[condition, t, f] или If[condition, t, f, u]
Если условие дает  , то выполняется часть
, то выполняется часть 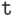 , если условие дает
, если условие дает  , то выполняется часть
, то выполняется часть  , если условие не дает ни
, если условие не дает ни  , ни
, ни  , то выполняется часть
, то выполняется часть  :
:
![\tt
In[167]:=abs[x\_ ]:=If[x < 0, -x,x] \\
\phantom{In[167]:=}Map[abs,\{1,0,-1,y\}] \\ \\
Out[168]=\{1,0,1,If[y < 0, -y,y]\} \\ \\
In[169]:= \\
\phantom{In}abs1[x\_]:=If[x >0,-x,x,"значение не сравнимо с нулем"] \\
\phantom{In}Map[abs1,{1,0,-1,y}] \\ \\
Out[170]={1,0,1, значение сравнимо с нулем}](/sites/default/files/tex_cache/e201207595a2ab7504a75585a3b2f3a5.png)
Оператор Which[test1, value1, test2, value2, ...]
Последовательно выполняет тесты, возвращая значение 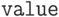 для первого теста, дающего
для первого теста, дающего  :
:
![\tt
In[171]:= a=2; Which[a==1,x,a==2,b,a==2,c] \\ \\
Out[171]=b](/sites/default/files/tex_cache/42eb198b4bc878886ea621a9551fefae.png)
Присвоение при условии lhs := rhs /; test
Присвоение происходит только в случае, если тест дает ![\text{\tt True (Condition[])}](/sites/default/files/tex_cache/c6994674f3e958fe6ea98cea939dd12e.png) :
:
![\tt
In[172]:=f[x\_{-}]:=$\sqrt{x}$ /;x $\ge$ 0 \\ \\
In[173]:=Map[f,{4,-4}] \\ \\
Out[173]={2,f[-4]}](/sites/default/files/tex_cache/70e6b7632839b824893a7cf2c4af153d.png)
Операторы цикла и контроля
- Оператор
![\text{\tt Do[expr, \{i, imax\}]}](/sites/default/files/tex_cache/4f7f4595fc3ff7c7736c5c4cbd79495c.png) выполняет
выполняет 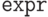 для всех
для всех 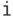 между
между 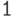 и
и  ;
; - Оператор
![\text{\tt Do[expr, \{i, imin, imax, di\}]}](/sites/default/files/tex_cache/97a5d2bdb3cf72114af3945541e44764.png) выполняет
выполняет 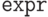 для всех
для всех 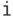 между
между  и
и  с шагом
с шагом 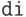 ;
; - Оператор
![\text{\tt Do[expr, \{i, list\}]}](/sites/default/files/tex_cache/0421a2a3cd8c020940628617e1a1b792.png) выполняет
выполняет 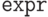 для всех
для всех 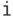 из списка
из списка  ;
; - Оператор
![\text{\tt Do[expr, \{i, \{n\}\}]}](/sites/default/files/tex_cache/678ebf592fbfe407531e8c5e5490ffcf.png) выполняет
выполняет 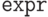 в количестве
в количестве  раз
раз
В приводимом ниже примере команда  выводит результат на экран:
выводит результат на экран:
![\tt
In[174]:=Do[res=$i^2$; Print[res],\{I,3\}} \\ \\ \tt
\phantom{In[174]:}1 \\ \\
\phantom{In[174]:}4 \\ \\
\phantom{In[174]:}9 \\ \\
\tt In[175]:=t=x;Do[t=1/(1+kt), \{k,2,6,2\}];t \\ \\
Out[175]=$\cfrac{1}{1+\cfrac{6}{1+\cfrac{4}{1+2x}}}$ \\ \\
In[176]:=Do[Print[$i^2$],\{i, \{3, 6, 8\}\}] \\ \\
\phantom{In[176]:}9 \\ \\
\phantom{In[176]:}36 \\ \\
\phantom{In[176]:}64 \\ \\
In[177]:=t-x;Do[t=1/(1+t),\{3\}];t \\ \\
Out[177]=$\cfrac{1}{1+\cfrac{1}{1+\cfrac{1}{1+x}}$](/sites/default/files/tex_cache/774e86f931e1d790afcb957aeae09576.png)
Вложенные циклы Do[expr, i1, ..., i2, ..., ...]
![\tt
In[178]:=Do[Print[{i,j}],{i, 4},{j, i-1}] \\ \\
\phantom{In[178]:}{2,1} \\ \\
\phantom{In[178]:}{3,1} \\ \\
\phantom{In[178]:}{3,2} \\ \\
\phantom{In[178]:}{4,1} \\ \\
\phantom{In[178]:}{4,2} \\ \\
\phantom{In[178]:}{4,3}](/sites/default/files/tex_cache/733bdb3deaa6d60316f52027b151f50e.png)