Практикум по компьютерной геометрии
[+]
Опубликован: 27.12.2010 | Доступ: свободный | Студентов: 1031 / 279 | Оценка: 5.00 / 5.00 | Длительность: 18:38:00
ISBN: 978-5-9556-0117-5
Темы: Математика, САПР
Специальности: Математик
Теги: алгебра, анализ, вычисления, геометрия, программное обеспечение
Лекция 4:

Детализация
A
|
версия для печати
< Лекция 3 || Лекция 4: 1234567 || Лекция 5 >
Аннотация: Подробно рассматриваются выражения, символы и контексты, определения и шаблоны.
Ключевые слова: заголовки, команда, выражение, целое число, список, правило вывода, доступ, полное имя, контекст, package, вычисление, функция, определяющее выражение

Выражения - универсальный конструктор в Mathematica

Напомним, что f[x,y,...] - универсальный (канонический) вид выражения, где x, y,... могут быть выражениями или атомарными объектами (числами, символами, строками).

Последовательность аргументов x, y, ... называется Sequence.

In[1] :=f [Sequence [x,у,z] ]
Out[1]=f[x,y,z]
In[2]:=f [x, Sequence [y,z],w]
Out[2] = f [x,y,z,w]

f называется заголовком ( Head ) выражения f[x, y, ...]. Заголовок f может быть как символом, так и более сложным выражением (в приведенных ниже примерах заголовки - это f[2] и (a+b) ):

In[3]:=f [2][х,у] 
      (а + Ь)[х]
Out[3] =f[2][х, у]
Out[4] =(а+b)[х]

Еще пример: заголовком является InterpolatingFunction[{{0.,3.}},<>] (команда First - взятие первого элемента списка):

In[5]:=
     у/.First[NDSolve[{y''[х] == -у[х], у[0] == у'[0]==2} , 
      y,{х,0,3}]] 
     f[x] 
     f[2.3] 
     Plot[f[x],{x,0,3}]
Out[5] =InterpolatingFunction [{{0.,3.}}, <>]
Out[6] =InterpolatinqFunction [{f0.,3.}}, <>][х]
Out[7] =0.158858

In[9] := Clear [f]

Команда FullForm позволяет представить выражение в каноническом виде:

In[10]:=FullForm [\frac{x+y-zw)}{a+(b-c)^{\frac12}}] 
Out[10] =
     Times[Power[
       Plus[a,Power[Plus [b, Times[-1, c]],Rational[1, 2]]],
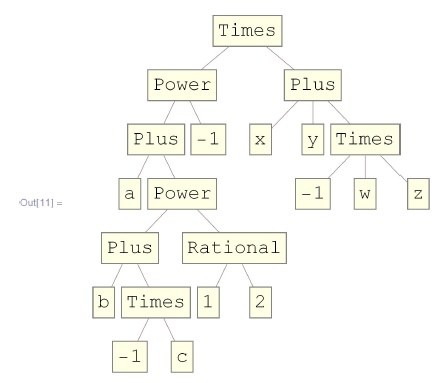
         -1],Plus[x,y,Times[-1,w,z]]]

Выражения имеют структуру дерева:

In[11]:= TreeForm[\frac{x+y-zw}{a+(b-c))^{\frac12}}]

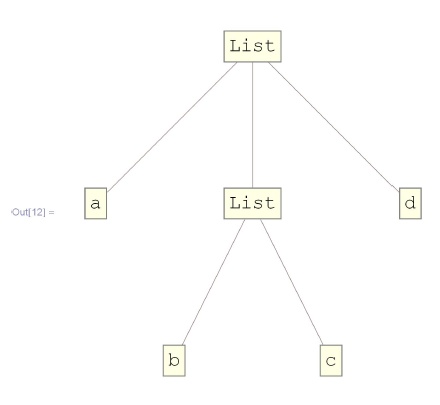
Список, как частный случай выражения, тоже имеет структуру дерева:

In[12]:=TreeForm[{a,{b,с},d}]

Если в одной скобке стоит последовательность выражений 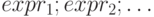expr_1; expr_2; \dots, разделенных точкой с запятой, то на самом деле там имеется одно выражение CompoundExpression[expr_1; expr_2; \dots ] . Например, последовательность выражений

In[13]:=х=2; у=х2;
        y
0ut[14]=4

представляет собой одно выражение

In[15]:=CompoundExpression[х=2,у=х2,у]
Out[15]=4
In[16]:=Clear[x,у]

Уровни выражения expr

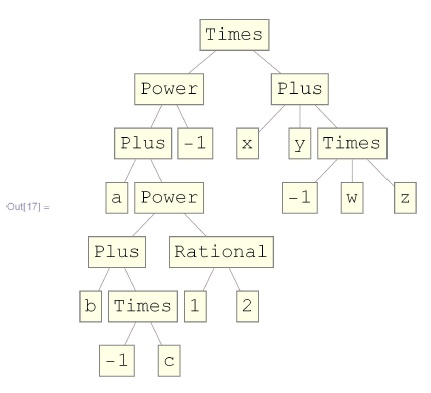
Каждое выражение разбито на уровни. Посмотреть на них можно с помощью команды Level[expr,levelspec], где levelspec описывает интересующие уровни:

In[17]:=TreeForm [\frac{x+y-zw}{a+(b-c)^{\frac12}}]

In[18]:= Table [Level \left [ \frac{x+y-zw}{a+(b-c)^{\frac 12}} , \{i\}\right ], \{i, 0, 7\}]\\ Out[18] =\\ \left \{ \left \{ \frac{x+y-wz}{a+\sqrt{b-c}}\right \},\left \{ \frac{1}{a+\sqrt{b-c}}, x+y-wz \right \}, \{a+\sqrt{b-c}, -1 x, y, -wz\},\\ \begim{matrix} &\{a, \sqrt{b-c}, -1, w,z\}, \{b-c, \frac 12\}, \{b, -c\}, \{-1, c\}, \{\}\} \end{matrix}

levelspec ={n} - только n -й уровень (нулевой уровень - само выражение):

In[l9]: = Level \left [ \frac{x+y-zw}{a+(b-c)^{\frac 12}}, \{3\} \right]\\ Out[l9]=\{a, \sqrt{b - с} , -1, w, z\}

levelspec = n - все уровни от 1-го до n -го (нулевой уровень не включен):

In[20]: = Level \left [ \frac{x+y-zw}{a+(b-c)^{\frac 12}}, 3\right]\\ Out[20] = \{a, \sqrt{b - с} , а + \sqrt{b - с} , -1,\\ \begin{matrix} &&&\frac{1}{a+\sqrt{b-c}^{\frac 12}}, х, у, -1, w, z, -w z, x+y-wz\} \end{matrix}

levelspec = {n, m} - уровни с номерами между n и m:

In[21]:= Level \left [\frac{x+y-zw}{a+(b-c)^{\frac 12}}, \{3, 5\}] Out[21] = \{а, b, -с, b - с, \frac 12, \sqrt{b - с} , -1, w, z\}

levelspec = {n, Infinity} - уровни с номерами, не меньшими, чем n:

In[22]: = Level \left [ \frac{x+y-zw}{a+(b-c)^{\frac 12}} , \{0, Infinity\} \right]\\ Out[22] =\{a, b, -1, с, -с, b - с, \frac 12, \sqrt{b - с} , a + \sqrt{b - с} , -1,\\ \begin{matrix} &&&\frac{1}{a+\sqrt{b-c}}, x, у, -1, w, z, -wz, x + y-wz, \frac{x+y-wz}{a+\sqrt{b-c}}\} \end{matrix}
Дальше >>
< Лекция 3 || Лекция 4: 1234567 || Лекция 5 >

Вопросы и ответы

вопросов: 0