Детализация
Атрибуты
Атрибуты служат для задания некоторых специальных неявных свойств функций, таких как коммутативность ( Orderless ), ассоциативность ( Flat ) и другие. Имеется 19 типов возможных атрибутов (см. Help ). Посмотреть атрибуты объекта можно командой Attributes[x]:
In[199] : = Attributes [Plus]
Out[199]= {Flat, bistable, NumericFunction,
Oneldentity, Orderless, Protected}Задать атрибуты для x можно так: Attributes[x] ={attr1, attr2, ...}:
In[200]:=С1еагА11 [f, x]
In[201]:=f [{1, 2, 3}]
Out[201] = f [{1, 2, 3}]
In[202]:=Attributes [f] = {Listable}
f [{1, 2, 3}]
Out[202]= {Listable}
Out[203] = { f [ 1 ] , f [2], f [3]}Добавить атрибут attr для x можно командой SetAttributes[x,attr]:
In[204]:=f [f [x, y] , z]
Out[204] = f [f [x, y] , z]
In[205]:=SetAttributes[f, Flat]
f[f[x, y],z]
Out[206] = f [x, y, z]Удалить атрибут attr из списка атрибутов объекта x можно командой ClearAttributes[x, attr]:
In[207]:=ClearAttributes [f, Flat]
f[f[x, y], z]
Out[208] = f [f [x, y] , z]Полный список атрибутов символов в пакете Mathematica:
-
Orderless - коммутативность функции:
In[209]:=f [х, у] == f [у, х] Out[209] = f [x, у] ==f[y, x] In[210] := SetAttributes [f, Orderless] f [х, у] == f[y, x] Out[211] = True In[212]:=f [f [x, y] , z] Out[212] = f [z, f [x, y] ] -
Flat - "обобщенная" ассоциативность функции (обобщенная в том смысле, что f[f[...[x]]] отождествляется с f[x] ):
In[213]:=f [f [х, у] , z] f[f[f[x]]] Out[213] = f [z, f [x, y] ] Out[214] = f [f [f [x] ] ] In[215] := SetAttributes [f, Flat] f[f[f[x]]] f[f[x, y], z] Out[216] = f [x] Out[217] = f [x, y, z] In[2l8]:= {f [f [a, a, a] , a] , f [f [f [a] , f [a] , f [a]] , a]} Out[218] = {f [a, a, a, a], f[a, a, a, a]}Проиллюстрируем особенности взаимодействия функции с атрибутами Flat и Orderless и замены:
In[219]:= f [a, b, с, d, e] /. f[b, с, d] -> х Out[219] = f[a, e, x]
Здесь сначала f[a, b, c, d, e] отождествляется с f[a, f[b, c, d], e] и после делается замена. Аргументы x и e в результирующем выражении переставлены в силу коммутативности.
Еще пример:
In[220]:= f [а, Ь, с, d, e] /. f[b, с, d] -> f[x, у] Out[220] = f [a, e, х, у]
Здесь после замены f[a, b, c, d, e] на f[a, f[x, y], e] последнее выражение отождествляется с f[a, x, y, e].
-
OneIdentity - наличие этого атрибута приводит к тому что выражение f[f[...f[a]]] заменяется на a внутри другой функции. Работает обычно совместно с атрибутом Flat.
In[221]:= SetAttributes[f, Flat] f [a, a, a, a] /. f[x_, x_, x_] -> g[x] Out[222] = f [a, g[f [a] ] ] In[223]:= f [a, b, c, d] /. f [x_, y_, z_] -> g[z] Out[223] = g[f [c, d] ] In[224] : = Attributes [f ] Out[224]= {Flat, bistable, Orderless}В предыдущем примере атрибут Flat позволяет отождествить выражение f[a, a, a, a] с обоими выражениями: как с f[f[a, a, a], a], так и с f[f[f[a], f[a], f[a]], a]. Если нет атрибута OneIdentity, то происходит отождествление с f[f[f[a], f[a], f[a]], a], таким образом, внутренняя функция f[f[a], f[a], f[a]] заменяется, в итоге, по правилу f[x_, x_, x_] \to g[x] на g[f[a]]:
In[225] := SetAttributes [f, Oneldentity]\\ f [a, a, a, a] /. f[x_, x_, x_] -> g[x] Out[226] = f [ a, g [ a ] ]Теперь установлен атрибут OneIdentity, поэтому выбирается отождествление с f[f[a, a, a], a], что приводит к замене f[a, a, a] на g[a].
-
Listable - функция, примененная к списку, автоматически применяется к каждому аргументу списка:
In[227]:=f [{1, 2, 3}] Out[227]= { f [ 1 ] , f [2], f [3]} In[228] := SetAttributes [f, bistable] f [{1, 2, 3}] Out[229] ={ f [ 1 ] , f [ 2 ] , f [ 3 ] } -
Constant - все производные функции равны нулю:
In[230]:=Dt[f] Out[230] = Dt [f ] In[231]:= SetAttributes [f, Constant] Dt[f] Dt[f g] Out[232] = 0 Out[233] = f Dt [g] In[234] : = Attributes [π] Dt[π] Out[234]= {Constant, Protected, ReadProtected} Out[235] = 0 -
NumericFunction - предполагается, что функция принимает числовые значения при условии, что ее аргументы - числа. В приводимом ниже примере NumericQ[expr] дает True, если выражение expr числовое, и False в противном случае:
In[236]: = NumericQ[f [x] ] NumericQ[f[2]] Out[236] = False Out[237] = False In[238] := SetAttributes [f, NumericFunction] NumericQ[f[x]] NumericQff[2]] Out|239] = False Out[240] = True -
Protected - определения функции не могут изменяться:
In[241]:=f [х_] := х2 f[2] SetAttributes [f, Protected] Out[242] = 4 In[244]:=f [x_] : = x3 f[2]SetDelayed::write: Tag f in f[x_] is Protected. >>
Out[244] = $ Failed Out[245] = 4 In[246]:=ClearAttributes [f, Protected] ; f [x_] : = x3 f[2] Out[248] = 8 -
Locked - атрибуты функции не могут изменяться до конца текущей сессии Mathematica. Использование одновременно Protected и Locked запрещает менять функцию до конца сессии:
In[249] := SetAttributes [f, Locked] ClearAttributes[f, Locked]Attributes::locked: Symbol f is locked. >>
-
ReadProtected - определение функции скрыто:
In[251]:=g[x_] := x2 ?gg g[x_] := x2 In[253]:=g[x_] := x2 SetAttributes[g, ReadProtected] ?gAttributes[g] = {ReadProtected} In[256]:=g[x_] := x3 ?gAttributes[g] = {ReadProtected} In[258]:= ClearAttributes [g, ReadProtected] ?gg[x_] := x3
-
HoldFirst - первый аргумент функции не вычисляется:
In[260]:= SetAttributes [h, HoldFirst] h[l + 1, 2+2, 3 + 3] Out[261] =h[l + 1, 4, 6]В следующем примере ошибка возникает из-за того, что аргумент х сначала вычисляется, а потом уже обрабатывается функцией g. Поэтому происходит попытка присвоить числу 17 значение 25. Этой ошибки можно избежать с помощью атрибута HoldFirst:
In[262]:=g[sym_, val_] := (sym=val^2) x = 17; g[x, 5] xSet::setraw: Cannot assign to raw object 17.<<
Out|264] = 25 Out[265] = 17 In[266]:=SetAttributes [g, HoldFirst] ; g[x, 5] x Out[267] = 25 Out[268] = 25Аргумент все-таки можно вычислить, если применить к нему функцию Evaluate:
In[269] :=h [Evaluate [1 + 1] , 2 + 2, 3 + 3] Out[269] = h [ 2 , 4, 6 ]
- HoldRest - все аргументы функции, кроме первого, не вычисляются.
- HoldAll - все аргументы функции не вычисляются.
-
HoldAllComplete - все аргументы функции не вычисляются ни при каких обстоятельствах, например, даже при применении функции Evaluate:
In[270] := SetAttributes [h, HoldAllComplete] h[l + 1, 2 + 2, 3 + 3] h [Evaluate [1 + 1] , 2 + 2 , 3 + 3] Out[271] = h[l + 1, 2 + 2, 3 + 3] Out[272] = h [Evaluate [1 + 1], 2 + 2, 3 + 3] -
NHoldFirst - первый аргумент функции не подвергается обработке функцией N, переводящей числа в их приближенные десятичные записи.
В следующем примере вычисляется разложение в ряд Тейлора длины k для функции cos[x] в точке
, являющейся решением уравнения cos[x] = x. Решение этого уравнения находится с помощью функции FixedPoint[f,x], которая вычисляет значение f(f(… f(x))) до тех пор, пока оно не перестает меняться. Начальное значение x в рассматриваемом случае приходится задавать в виде десятичной дроби, иначе FixedPoint пытается все вычислять точно и не срабатывает. Тест ?InexactNumberQ как раз возвращает True, если его аргумент - десятичная дробь:In[273] :=ff [k_Integer, х_?InexactNumberQ] : = Module[{x0}, x0 = FixedPoint[Cos, х] ; Series [Cos [t] , {t, x0 , k}] ] ; gg[k_Integer, x_?InexactNumberQ] := Module[{x0}, x0 = FixedPoint[Cos, x] ; Series[Cos[t] , {t, x0 , k} ] ] ; SetAttributes[ff, NHoldFirst]; In[276]:={ff [2, 1.] , gg[2, 1.], ff[2, 1] , gg[2, 1]} Out[276] = {0.739085-0.673612 (t - 0 . 739085) - 0.369543 (t-0.739085)2+O[t-0.739085]3, 0.739085- 0.673612 (t - 0.739085) -0.369543 (t - 0.739085)2 + 0[t - 0.739085]3, ff[2, 1], gg[2, 1]}Мы видим, что обе функции ff и gg работают, если их аргументы имеют правильный тип, и не работают, если второй аргумент - целое число. Можно попробовать исправить последнее, применив функцию N. Но тогда первый аргумент функции gg перестанет быть целым и она снова не сработает, а функция ff сработает, так как ее первый аргумент не обрабатывается функцией N благодаря установленному атрибуту NHoldFirst.
In[277]: = N@{ff [2, 1] , gg[2, 1]} Out[277] = {0.739085-0.673612 (t-0.739085) - 0.369543 (t - 0.739085) 2 + 0[t - 0.739085] 3, gg[2., 1 .] } - NHoldRest - все аргументы функции, кроме первого, не подвергаются обработке функцией N.
- NHoldAll - все аргументы функции не подвергаются обработке функцией N.
-
SequenceHold - объекты типа "последовательность" ( Sequence ) не встраиваются в функцию.
In[278]:= hh[a, Sequence [b, с]] Out[278] = hh [ a, b, с ] In[279] := SetAttributes [hh, SequenceHold] hh[a, Sequence[b, c] ] Out[280]=hh [a, Sequence [b, c] ] -
Temporary - локальная переменная уничтожается, как только перестает использоваться:
In[281]: = Module[{x} , Print [х] ; Attributes [x] ] x$866 Out[281]= {Temporary} - Stub - признак того, что символ закреплен за некоторым пакетом Package, который автоматически загружается при явном использовании этого символа.
Символы с атрибутом Stub создаются с помощью команды DeclarePackage[<пакет>,<имя или список имен>] >:
In[282] :=DeclarePaakage ["ErrorBarPlots' ", "ErrorListPlot"] Out[282] = ErrorBarPlots'
В результате символ ErrorListPlot получает контекст ErrorBarPlots, который становится первым в списке контекстов. Кроме того, если теперь будет выполнена функция с именем ErrorListPlot, то до ее вычисления с помощью функции Needs будет загружен пакет ErrorBarPlots:
In[283] : = Attributes ["ErrorListPlot"]
Out[283]= {Stub}
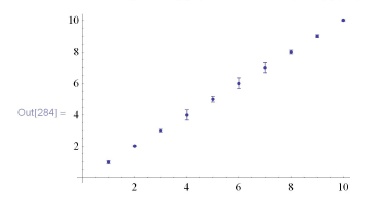
In[284] : =
ErrorListPlot[Table [ {i, RandomReal [0.5]} , {i, 10}]]
Можно также определить свою функцию, использующую функции из какого-нибудь (одного) пакета:
In[285]:=DeclarePackage["Combinatorica ' ", "tc"] ;
In[286] := tc [x_]: = ToCycles [x] ;
In[287]:=tc[{l, 2, 3, 4, 5, 6, 7, 8, 9, 10}]
Out[287] = { {1} , {2}, {3}, {4}, {5}, {6}, {7}, {8}, {9}, {10}}
In[288]:=ClearAll[ff, gg, g, h, hh, tc]