Кривые и поверхности в компьютерной геометрии, I
Введение: зачем и как нужно интерполировать
Первая проблема, с которой сталкиваются математики, работающие в приложениях, состоит в том, что предлагаемые им исходные данные устроены совсем не так, как их учили на некоторых теоретических и механических курсах на механико-математическом факультете Московского государственного университета им. М.В. Ломоносова. Нет ни функций, ни формул, есть просто результаты тех или иных измерений, представляющие собой числа, организованные с той или иной степенью разумности. В частности, при решении прикладных геометрических задач мы получаем на входе координаты точек в трехмерном пространстве, которые нам самим предстоит организовать в кривые или поверхности. Поэтому каждый раз приходится начинать с решения задачи интерполяции, которая как раз и состоит в восстановлении кривой или поверхности по данному набору точек. При этом полученная в результате кривая или поверхность должны обладать разумными математическими свойствами (например, быть дважды непрерывно дифференцируемой), не отходить дал еко от исходных точек, а также выглядеть достаточно эстетично. Ясно, что от того, насколько хорошо мы справимся с этой задачей, зависит точность и эффективность всех наших дальнейших расчетов. Тем самым интерполяция имеет первостепенное значение в приложениях.
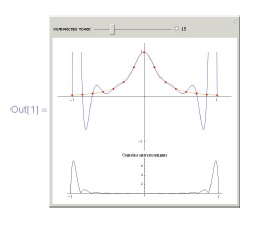
Рассмотрим простой пример. На первом курсе вам рассказывали, как интерполировать график функции одного вещественного переменного с помощью интерполяционного многочлена. Для этого, напомним, надо выбрать на графике (n + 1) точку и построить единственный многочлен степени n, график которого через эти точки проходит. При этом качество полученной интерполяции существенно зависит от расположения выбранных точек. Если выбрать точки на графике, например равномерно, то отклонение итогового многочлена от приближаемой функции может расти с ростом степени полинома:
In[1] := DynamicModule {RungePlot, г, Runge, x} ,
Manipulate[RungePlot[n],
{{n, 15, "количество точек"}, 5, 50, 5,
Appearance -> "Labeled" , ControlPlacement -> Bottom} ,
SaveDefinitions -> True] ,
Initialization: -> ( r[x_] := 1/(1+25x2);
Runge[n_] := Table[
{x, r[x]}, {x, -1., 1., 2. / (n-1)}];
RungePlot[n_] :=Module[{data, interp},
interp = Expand[
InterpolatingPolynomial[Runge[n] , x] ] ;
Column[{Plot[{1/ (l + 25x^2), interp}, {x, -1, 1},
ImageSize -> {300} , Epilog -> {
PointSize [Medium] , Red, Point/@ Runge [n] } ,
PlotStyle-> {Orange, Blue}, PlotRange-> {-1, 1},
Ticks -> {{-1, 1} , {-1, 1}} ,
ImageSize -> 300, PlotRangePadding -> .2] ,
ListLinePlot[Table[{x, Abs[N[N[interp] - r[x]]]},
{x, -1, 1, .01}] ,
ImageSize -> 300, PlotRange -> All,
Ticks -> { { -1, 1} , Automatic} ,
PlotLabel -> "Ошибка интерполяции" ,
PlotStyle -> Black, AspectRatio -> .25,
ImageSize -> 300] } , Center] ] ) ]Проиллюстрированный здесь эффект носит название феномена Рунге.
Преодолеть эту трудность можно с помощью более хитрого выбора точек на графике. Так например, если выбирать точки известным методом Чебыше-ва, то для аналитических функций погрешность убывает с ростом степени многочлена как геометрическая прогрессия. Другой широко применяемый метод состоит в использовании кусочно-полиномиальных интерполяционных функций - так называемых сплайнов.
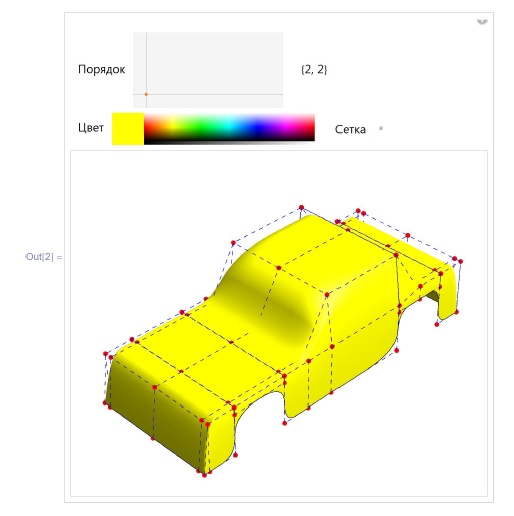
В дословном переводе слово spline означает лекало или рейку используемую в строительных или морских конструкциях. Впервые понятие сплайна как кусочно-полиномиальной функции было введено Исааком Шенбергом (1903-1990, Румыния, США) в 1943-1946 годах при решении прикладных задач для американских ВВС, а затем и в теоретических исследованиях. Широкую известность и применение сплайны нашли после того, как в 60-е годы прошлого века французские математики-прикладники Пьер Безье, работавший на Рено, и Поль де Кастелье, работавший на Ситроен, независимо применили их для создания первых САПР в автомобилестроении. Конечно, мы не знаем точно, как выглядела их программа, но суть ее, вероятно, сводилась к следующей демо-версии:
In[2] :=DynamicModule [ {color, carbody, degrees, mesh},
Manipulate[
Graphics3D[{
color, Specularity[White, 50] ,
BSplineSurf ace [carbody , SplineDegree -> Floor [degrees] ] ,
If[mesh,
{Dashed, Blue, Line[carbody], Line[Transpose[carbody]],
Red, PointSize [Medium] , Point /@ carbody} , { } ] } ,
Boxed -> False, Lighting -> "Neutral" , RotationAction -> "Clip" ,
Viewpoint -> {-2,-2,2}],
Row[
{Control [{{degrees, {2, 2}, "Порядок"}, {1, 1}, {14, 7},
ImageSize-> {140, 70}}],
Dynamic[Floor[degrees]]}, Spacer[10]],
Row[
{Control[{{color, Yellow, "Цвет"},
ColorData["HTML", "GoldenRod"]}],
Control[{{mesh, True, "Сетка"}, {False, True}}]}, Spacer[10]]
] , Initialization :-> (carbody = {
{{-.2, -2.25, 0}, {-.2, -2.25, 0}, {-.2, -2, 0}, {-.2, 0, 0},
{-.2, 2, 0}, {-.2, 2.25, 0}, {-.2, 2.25, 0}},
(* \dots еще тринадцать семерок точек \dots *)
{{11.01, -2.25, 0}, {11.01, -2.25, 0}, {11.01, -2, 0},
{11.01,0,0}, {11.01,2,0}, {11.01,2.25,0}, {11.01,2.25,0}}
})Инженер-проектировщик задает контуры будущего автомобиля набором точек, которые отражают лишь основные функциональные особенности (наличие четырех колес, кабины, капота и пр.). Затем программа строит по эти точкам поверхность-сплайн, свойствами которого (в нашем примере - степенями многочленов-кусков по координатам) можно управлять. После того как сплайн выбран, начинается работа по деталировке.
На первых нескольких занятиях этого семестра мы познакомимся с базовыми понятиями современной теории сплайнов. Разумеется, у нас нет времени сколько-нибудь углубляться здесь в подробности. Современная теория сплайнов представляет собой хорошо разработанную, разветвленную и сложную науку. Заинтересовавшиеся слушатели приглашаются на спецкурс кафедры Дифференциальной геометрии и приложений Компьютерная геометрия, который читают Д.П. Ильютко и Г.В. Носовский. См. также книгу Н. Н. Голованова, Д. П. Ильютко, Г. В. Носовского, А. Т. Фоменко, Компьютерная геометрия [1].
Мы начнем с одномерного случая.