НОУ ИНТУИТ | Практикум по компьютерной геометрии. Лекция 5: Кривые и поверхности в компьютерной геометрии, I

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

Опубликован: 27.12.2010 | Доступ: свободный | Студентов: 1030 / 278 | Оценка: 5.00 / 5.00 | Длительность: 18:38:00

ISBN: 978-5-9556-0117-5

Темы: Математика, САПР

Специальности: Математик

Теги: алгебра, анализ, вычисления, геометрия, программное обеспечение

|

Вам нравится? Нравится 14 студентам

| Поделиться |

Поддержать курс

| Скачать электронную книгу

Кубические сплайны

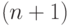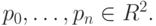Пусть дана (n + 1) точка $p_0, \dots ,p_n \in R^2.$ Требуется провести через эти точки кривую класса 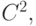C^2, т. е. имеющую непрерывные первые и вторые производные радиус-вектора по параметру: 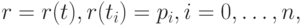$r = r(t), r(t_i) = p_i, i = 0, \dots , n,$ и $\dot r(t), \ddot r(t)$ - непрерывны по 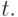Решение этой задачи можно дать в виде кубического сплайна. На каждом участке $[t_i,t_{i+1}]$ такой сплайн описывается полиномом третьей степени по 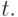При полиномиальной интерполяции степень полинома в данной задаче не может быть, вообще говоря, сделана меньше 3. Поэтому кубический сплайн имеет наименьшую степень в данной постановке задачи и определяется однозначно.

Пусть искомый сплайн задается параметрическим уравнением 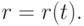r = r(t) . Обозначим 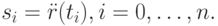$s_i = \ddot r(t_i ), i = 0, \dots , n.$ Поскольку сплайн является кубическим, вторая производная радиус-вектора будет линейной функцией на каждом отрезке $[t_i,t_{i+1}]$ :

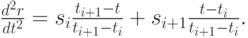$\frac{d^2r}{dt^2}=s_i \frac{t_{i+1}-t}{t_{i+1}-t_i}+s_{i+1}\frac{t-t_i}{t_{i+1}-t_i}.$

( 5.12)

Проинтегрируем (5.12) два раза. Получим

$r(t)=s_i \frac{(t_{i+1}-t)^3}{6(t_{i+1}-t_i)}+s_{i+1}\frac{(t-t_i)^3}{6(t_{i+1}-t_i)}+c_1t+c_2$

( 5.13)

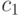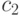Постоянные c_1 и c_2 определим из условий, заданных на концах данного участка кривой:

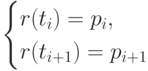$\begin{cases} r(t_i)=p_i,\\ r(t_{i+1})=p_{i+1} \end{cases}$

( 5.14)

Подстановка (5.13) в (5.14) и вычисление c_1, c_2 приводит к следующему ответу:

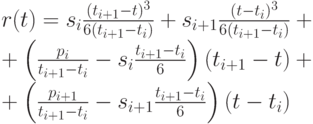$r(t)=s_i \frac{(t_{i+1}-t)^3}{6(t_{i+1}-t_i)}+s_{i+1} \frac{(t-t_i)^3}{6(t_{i+1}-t_i)}+\\ +\left( \frac{p_i}{t_{i+1}-t_i}- s_i \frac{t_{i+1}-t_i}{6}\right)(t_{i+1}-t)+\\ + \left( \frac{p_{i+1}}{t_{i+1}-t_i}-s_{i+1} \frac{t_{i+1}-t_i}{6}\right) (t-t_i)$

( 5.15)

Правая часть (5.15) является кубическим полиномом по на отрезке $[t_i,t_{i+1}].$ Она содержит два неизвестных векторных параметра s_i и $s_{i+1}.$ Их можно определить из условия согласованности первых производных на концах отрезков $[t_i,t_{i+1}].$ Пока мы еще не использовали этого условия (вторые производные уже согласованы в силу определения si). На левом конце отрезка $[t_i,t_{i +1}]$ мы имеем

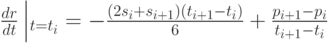$\frac{dr}{dt} \left |_{t=t_i}=- \frac{(2s_i+s_{i+1})(t_{i+1}-t_i)}{6}+\frac{p_{i+1}-p_i}{t_{i+1}-t_i}$

( 5.16)

Аналогично, на правом конце отрезка $[t_{i-1},t_i] ,$ т.е. в той же точке t_i, имеем

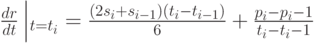$\frac{dr}{dt} \left |_{t=t_i}= \frac{(2s_i+s_{i-1})(t_i-t_{i-1})}{6}+\frac{p_i-p_i-1}{t_i-t_i-1}}$

( 5.17)

Приравнивая правые части (5.16) и (5.17), получим 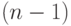(n - 1) уравнение для внутренних точек $i = 1, \dots ,n-1$ :

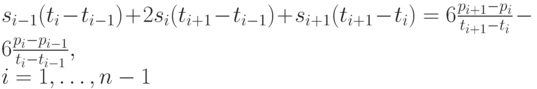$s_{i-1}(t_i-t_{i-1})+2s_i(t_{i+1}-t_{i-1})+s_{i+1}(t_{i+1}-t_i)=6\frac{p_{i+1}-p_i}{t_{i+1}-t_i}-6 \frac{p_i-p_{i-1}}{t_i-t_{i-1}},\\ i=1, \dots, n-1$

( 5.18)

Система (5.18) представляет собой систему из 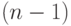(n - 1) векторного уравнения (или, что то же самое, 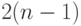2(n - 1) скалярного уравнения) с ленточной трехдиагональной матрицей и 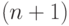(n+1) векторных неизвестных 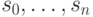$s_0, \dots , s_n$ (что соответствует 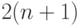2(n+ 1) скалярных неизвестных). Если кривая замкнута, то s_0 = s_n и в систему (5.18) добавляется еще одно уравнение для i = n :

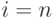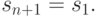
$s_{n+1}=s_1.$

Таким образом, для замкнутой кривой число неизвестных равно числу уравнений и система имеет единственное решение.

Если кривая незамкнута, то необходимо задать граничные условия. Например, если рассматривать сплайны как гибкую нить, концы которой не имеют нагрузки на изгиб, получим такое условие:

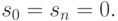( 5.19)

Еще один возможный вариант граничных условий:

$s_0 = s_1, s_n = s_{n-1}$

( 5.20)

В последнем случае концевые участки кривой будут иметь постоянную кривизну.

Определив из системы (5.18) и граничных условий вида (5.19) или (5.20) (или каких-либо других, следующих из постановки задачи) значения 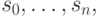$s_0, \dots , s_n,$ получим формулу для искомого кубического сплайна на участке $[t_i, t_{i+1}]$ :

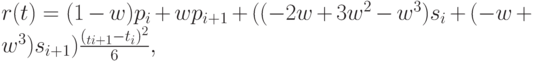
$r(t) = (1 - w)p_i + wp_{i+1} +((-2w + 3w^2 - w^3 )s_i + (-w + w^3 )s_{i+1} )\frac{(_{ti+1}-t_i)^2}{6},$

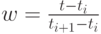где $w =\frac{t-t_i}{t_{i+1}-t_i}$ - местный параметр на участке $[t_i,t_{i+1}].$

Замечание 5.2.1.

В отличие от составного сплайна Эрмита, для кубического сплайна изменение положения одной из опорных точек всегда приводит к перевычислению всего сплайна.
Если взять равномерную параметризацию, т. е. положить 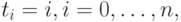$t_i = i, i = 0, \dots ,n,$ то уравнения (5.18) примут совсем простой вид:

$s_{i-1} + 4s_i + s_{i+1} = 6(p_{i+1} - 2p_i + p_{i-1}), i = 1, \dots , n - 1.$

Однако равномерная параметризация в случае неравномерного расположения опорных точек может привести к появлению необоснованных изгибов сплайна. Для того чтобы сплайн не имел подобных изгибов, параметризацию следует выбирать приблизительно натуральной. Для этого достаточно потребовать выполнения приблизительного равенства:

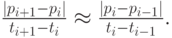
$\frac{|p_{i+1}-p_i|}{t_{i+1}-t_i} \approx \frac{|p_i-p_{i-1}|}{t_i-t_{i-1}}.$

Сплайны в пакете Mathematica. Для создания сплайнов используется подпакет SplineFit, просто надо загрузить Splines' из Splines Package. Для этого используется функция SplineFit[data, type] , которая возвращает сплайн для данных data, используя сплайн-аппроксимацию типа type - по умолчанию это кубический сплайн Cube (другие типы - Bezier и CompositeBezier ).

Пример 5.2.5. Кубический сплайн с шестью управляемыми мышью опорными точками:

In[6] : = DynamicModule [ {pts , pts0, n = 6, spline},
                   Pts0= {{6.0, -5.0}, {0.0, 0.0}, {4.8, 5.2}, {20.3, 10.5}, {6.8, 12.2}, 
                         {20.0, 20.0}}; 
                   Manipulate[Show[{
                            ParametrioPlot[spline[pts][x], {x, 0, 6}, 
                              PlotStyle -> {Thick}] , Graphics [ {Red, 
                                Text[ToString[#- 1] ,
                                    pts[[#]] + {1.4, 0}] & /@ Range [n] }} } , 
                          PlotRange ->{{-l,23}, {-6, 21}}], 
                      {{pts, ptsO}, Locator}], 
                   Initialization : -> ( 
                        Needs["Splines'"]; 
                         spline[pfcs_] := SplineFit[pts, Cubic])]

Дальше >>

Авторизоваться

Практикум по компьютерной геометрии

Кривые и поверхности в компьютерной геометрии, I

Кубические сплайны

Вопросы и ответы