|
Добрый день. Я приступила сегодня к самостоятельному изучению курса "Моделирование систем". Хочу понять - необходимо ли отсылать мои решения практических заданий на сайт, (и если да - то где найти волшебную кнопку "Загрузить...") или практические задания остаются полностью на моей совести? (никто не проверяет, и отчётности по ним я предоставлять не обязана?) P.S.: тьютора я не брала |
Планирование и обработка результатов пассивного эксперимента
Теоретическая часть
Основная задача пассивного эксперимента — по результатам наблюдений сделать некоторые выводы о параметрах математической модели эксперимента [1]. При этом вид ее предполагается известным, а параметры — неизвестными. Далее будет рассматриваться класс линейных регрессионных моделей эксперимента.
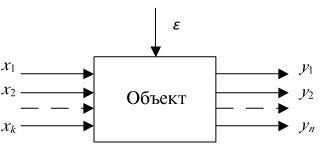
В общем случае объект исследования представляется в виде схемы, представленной на рис. 9.1, где 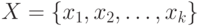 — входные величины или факторы;
— входные величины или факторы;  —
—  -я выходная величина (
-я выходная величина ( 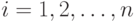 );
); 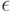 — случайные неконтролируемые возмущения [12].
— случайные неконтролируемые возмущения [12].
Под моделью объекта по  -му каналу понимают функцию
-му каналу понимают функцию
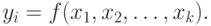 |
( 9.1) |
Так как имеются случайные неконтролируемые возмущения, изменение функции (9.1) носит случайный характер, а потому для получения математического описания (9.1) применяются методы регрессионного анализа на основе статистических данных, накопленных в результате проведения эксперимента.
Применение метода пассивного эксперимента может быть успешным, если при его проведении соблюдаются необходимые условия, к которым относятся такие, как правильное определение времени регистрации данных, обеспечение независимости соседних измерений и входных переменных друг от друга, достаточный с точки зрения математической статистики объем экспериментальных данных [12].
Если функция не имеет бесконечных разрывов, то ее можно разложить в степенной ряд Тейлора:
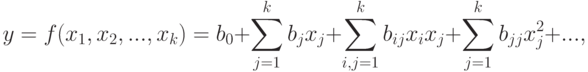 |
( 9.2) |
где 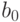 ,
, 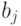 ,
, 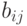 ,
, 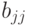 — постоянные коэффициенты уравнения, оценки которых необходимо определить в результате постановки и проведения пассивного эксперимента;
— постоянные коэффициенты уравнения, оценки которых необходимо определить в результате постановки и проведения пассивного эксперимента;  — число наиболее существенных входных величин, полученных в результате отсеивающего эксперимента.
— число наиболее существенных входных величин, полученных в результате отсеивающего эксперимента.
Пространство, в котором строится поверхность отклика – реакция выходной величины, называется факторным пространством .
Для применения методов регрессионного анализа требуется выполнение ряда предпосылок [12], а именно:
- результаты наблюдений
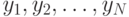 выходной величины в точках факторного пространства представляют собой независимые случайные величины, распределенные по нормальному закону, а процесс изменения выходной величины должен быть стационарным во времени;
выходной величины в точках факторного пространства представляют собой независимые случайные величины, распределенные по нормальному закону, а процесс изменения выходной величины должен быть стационарным во времени; - дисперсии
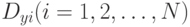 этих случайных величин должны быть равны друг другу (выборочные оценки дисперсий однородны);
этих случайных величин должны быть равны друг другу (выборочные оценки дисперсий однородны); - все значения входных величин должны измеряться с пренебрежимо малой ошибкой по сравнению с ошибкой измерения выходной величины;
- входные величины не должны коррелировать между собой;
- все соседние измерения по каждой
 -й входной величине должны быть независимы.
-й входной величине должны быть независимы.
Число коэффициентов уравнения (9.2) определяет объем эксперимента. Поэтому выбирают такой полином, который содержит как можно меньше коэффициентов, но удовлетворяет требованию простоты и адекватности, под которой понимается способность модели предсказывать результаты эксперимента в некоторой области с требуемой точностью.
Часто на предварительной стадии исследования объекта выбирают полином первой степени (включая первую сумму в уравнении (9.2), т. е. в разложении Тейлора), предполагая, что параметры объекта лежат в области, в которой расположен экстремум исследуемой функции (выходная величина системы – отклик), и поэтому объект описывается линейной моделью. Если же эта линейная модель оказывается неадекватной, то в нее включают члены парного взаимодействия 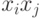 (включая вторую сумму в уравнении (9.2), т. е. в разложении Тейлора), а при необходимости увеличивают степень полинома до тех пор, пока модель не окажется адекватной [12].
(включая вторую сумму в уравнении (9.2), т. е. в разложении Тейлора), а при необходимости увеличивают степень полинома до тех пор, пока модель не окажется адекватной [12].
В результате регрессионного анализа результатов пассивного эксперимента находят оценки коэффициентов уравнения регрессии 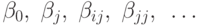 .
.
1. План эксперимента
Рассмотрим эксперимент, в котором проводится  измерений зависимой переменной
измерений зависимой переменной  в некоторых точках факторного пространства [1]. Обозначим через
в некоторых точках факторного пространства [1]. Обозначим через 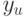 наблюдаемое значение зависимой переменной
наблюдаемое значение зависимой переменной  в
в  -м опыте в точке
-м опыте в точке
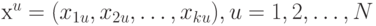 .
.
Здесь 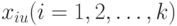 — значение переменной
— значение переменной  в
в  -м опыте.
-м опыте.
Определение 1. Набор точек 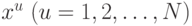 называется планом эксперимента. Точки при этом не обязательно должны быть различными. Матрица вида
называется планом эксперимента. Точки при этом не обязательно должны быть различными. Матрица вида
![X=\left[\begin{array}{cccc}
x_{11}& x_{21} &\ldots & x_{k1}\\
x_{12}& x_{22} &\ldots & x_{k2}\\
\ldots& \ldots &\ldots & \ldots\\
x_{1N}& x_{2N} &\ldots & x_{kN}
\end{array}
\right]](/sites/default/files/tex_cache/e5446b128b81147bf96298e5eb431b33.png) |
( 9.3) |
называется матрицей плана эксперимента.
Если обозначить различные точки плана через 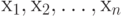 , то совокупность таких точек называется спектром плана.
, то совокупность таких точек называется спектром плана.
Определение 2. Нормированным планом 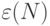 называют совокупность величин
называют совокупность величин 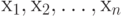 ;
; 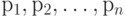 , где
, где 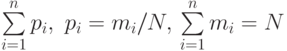 .
.
В пассивном эксперименте задача построения плана не рассматривается. Матрица плана (9.3) предполагается известной (заданной) или является предопределенной условиями проведения эксперимента [1]. Задача исследователя в пассивном эксперименте состоит в выполнении наблюдений над выходной (зависимой) переменной в точках, определяемых матрицей плана, и последующем анализе их результатов.
Примечание. В случае, когда регрессионная модель строится непосредственно по измерениям без предварительного усреднения, для того чтобы произвести оценку свободного члена, в модели необходимо представить матрицу плана в виде
![X=\left[\begin{array}{ccccc}
1&x_{11}& x_{21} &\ldots & x_{k1}\\
1&x_{12}& x_{22} &\ldots & x_{k2}\\
\ldots&\ldots& \ldots &\ldots & \ldots\\
1&x_{1N}& x_{2N} &\ldots & x_{kN}
\end{array}
\right]](/sites/default/files/tex_cache/f77429c19924ec5a274a3204709202bc.png) |
( 9.4) |
2. Одномерная регрессионная модель эксперимента
В общем случае вид функции отклика неизвестен. Будем предполагать, что функция отклика является одномерной и представима в виде
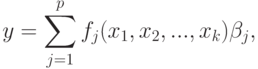 |
( 9.5) |
где:
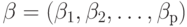 есть
есть  -мерный вектор неизвестных параметров;
-мерный вектор неизвестных параметров;
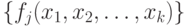 — известные функции, которые называются еще базисными функциями.
— известные функции, которые называются еще базисными функциями.
Под регрессионной моделью эксперимента будем понимать линейную по параметрам 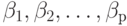 функцию отклика (9.5).
функцию отклика (9.5).
В качестве примера рассмотрим функцию отклика
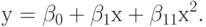
Построим матрицу планирования по заданным измерениям входной переменной 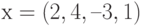 . В соответствии с (9.4) будем иметь
. В соответствии с (9.4) будем иметь
![X=\left[\begin{array}{ccccc}
1&2& 4\\
1&4& 16\\
1&-3& 9\\
1&1&1
\end{array}
\right] .](/sites/default/files/tex_cache/87bd9a7c3a156cc23490daa7917e4764.png)
Еще один пример. Пусть функция отклика имеет вид
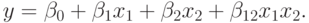
Значения независимых переменных равны следующим значениям:
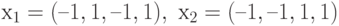 .
.
Тогда матрица планирования будет иметь такой вид, что в верхней строчке ее будут указаны аргументы функции отклика
![X=\left[\begin{array}{ccccc}
x_0&x_1& x_2 &x_1x_2\\
1&-1& -1 &1\\
1&1& -1 &-1\\
1&-1& 1 &-1\\
1&1& 1 &1\\
\end{array}
\right],](/sites/default/files/tex_cache/d992c2b5da746a312129d899f74e0595.png)
где 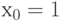 — фиктивная переменная.
— фиктивная переменная.
3. Оценивание параметров одномерной функции отклика
В случае, когда одномерная функция отклика является линейной относительно неизвестных параметров, т. е.
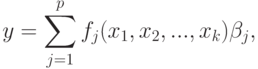
в произвольной точке 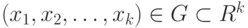 по результатам наблюдений (измерений) в точках
по результатам наблюдений (измерений) в точках 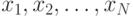 , где
, где 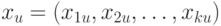 , задаваемых матрицей плана (планирования)
, задаваемых матрицей плана (планирования) 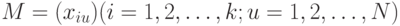 , наилучшая оценка в смысле метода наименьших квадратов равна
, наилучшая оценка в смысле метода наименьших квадратов равна
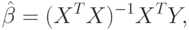 |
( 9.6) |
если ранг матрицы планирования равен числу неизвестных параметров, т. е. 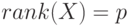 , где
, где  — число неизвестных параметров [1].
— число неизвестных параметров [1].
Оценка параметров по формуле (9.6) называется оценкой по наблюдениям полного ранга, т. е. когда 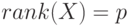 . В этом случае формула (9.6) вытекает из так называемого нормального уравнения
. В этом случае формула (9.6) вытекает из так называемого нормального уравнения
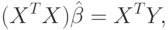 |
( 9.7) |
где  — информационная матрица.
— информационная матрица.
В методе наименьших квадратов минимизируется функционал (скалярная величина)
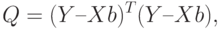 |
( 9.8) |
где 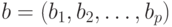 — вектор неизвестных параметров, подлежащих оценке.
— вектор неизвестных параметров, подлежащих оценке.
Оценка параметров по формуле (9.6) доставляет минимум функционалу (9.8). При подстановке (9.6) в (9.8) получающаяся величина называется остаточной суммой квадратов — RSS (Residual Sum of Squares).
4. Оценивание параметров многомерной функции отклика
В случае, когда имеются несколько выходных переменных — функций отклика, для каждой функции отклика можно произвести оценку параметров уравнения регрессии по формуле (9.6) с указанием нижнего индекса, относящегося к данной функции. Например, если имеется  функций отклика, то оценка вектора параметров по методу наименьших квадратов может быть найдена как
функций отклика, то оценка вектора параметров по методу наименьших квадратов может быть найдена как
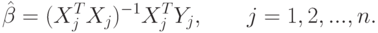 |
( 9.9) |
Общая оценка вектора параметров многомерной функции отклика будет определяться в виде
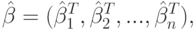 |
( 9.10) |
где  — символ транспонирования.
— символ транспонирования.