НОУ ИНТУИТ | Моделирование систем. Лекция 5: Исследование качества генераторов случайных чисел

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

Мордовский государственный университет имени Н.П. Огарева

Опубликован: 30.11.2010 | Доступ: свободный | Студентов: 3296 / 1995 | Оценка: 4.12 / 4.13 | Длительность: 14:37:00

ISBN: 978-5-9963-0352-6

Темы: Программирование, Алгоритмы и дискретные структуры

Специальности: Программист, Системный архитектор

|

Вам нравится? Нравится 32 студентам

| Поделиться |

Поддержать курс

| Скачать электронную книгу

Аннотация: Цель работы: изучить и практически освоить оценки качества генераторов случайных чисел (ГСЧ) в различных системах программирования по заданным теоретическим показателям, с помощью критериев согласия и с помощью нормированной автокорреляционной функции на предмет независимости случайных чисел.

Ключевые слова: значение, параметр, псевдослучайное число, среднеквадратичное отклонение, реальное значение, Относительной погрешностью, стандартное отклонение, GPSS, метод Фибоначчи, рекуррентного соотношения, конгруэнтные числа, псевдослучайная последовательность, первообразный корень, взаимно простые числа, нормированная корреляционная функция

Теоретическая часть

В практике моделирования и особенно в практике статистических испытаний приходится использовать случайные последовательности или просто случайные числа. При моделировании систем на ЭВМ программная имитация случайных воздействий любой сложности сводится к генерированию некоторых стандартных (базовых) процессов и к их последующему функциональному преобразованию. Получение случайных чисел с требуемым законом распределения обычно выполняется в два этапа:

Формирование физическим или программным методом случайного числа 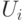$U_{i}$ , равномерно распределенного на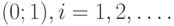
Программный переход от 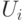$U_{i}$ к случайному числу 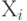$Х_{i}$ , имеющему требуемое распределение 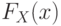$F_{X}(x)$ [16].

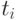В связи с этим особое значение приобретают случайные числа, равномерно распределенные в интервале [0; 1] . Например, генерирование экспоненциально распределенных случайных чисел $t_{i}$ может быть выполнено по формуле

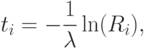
$t_i=-\frac{1}{\lambda}\ln(R_i),$

где:

$\lambda$ — параметр экспоненциального закона;

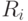$R_{i}$ — равномерно распределенное случайное число из интервала (0; 1) .

Существуют физические и программные датчики (генераторы) случайных чисел. Программные датчики случайных чисел фактически генерируют псевдослучайные числа. Согласно Лемеру, последовательность псевдослучайных чисел можно считать случайной, если "каждый ее член непредсказуем для непосвященного и она удовлетворяет ряду традиционных статистических тестов".

Полученные с помощью программных методов случайные последовательности в идеале должны состоять из:

равномерно распределенных,
статистически независимых,
воспроизводимых,
неповторяющихся чисел.

Практическая часть

1. Исследование качества генераторов случайных чисел (ГСЧ) по критерию отклонения математического ожидания, дисперсии среднего квадратического отклонения

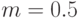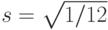Известно, что при равномерном законе распределения случайной непрерывной величины в интервале [0; 1] соответствующее математическое ожидание (m) , дисперсия $(s^{2})$ и среднеквадратичное отклонение (s) имеют следующие теоретические значения: m = 0.5 ; $s^{2} = 1/12$ ; s = 0.28867 ( $s=\sqrt{1/12}$ ).

Критерий заключается в сравнении теоретических параметров равномерного распределения с реальными значениями, полученными для конечной выборки.

1.1. Анализ качества ГСЧ системы MATLAB

В системе MATLAB всех версий используется функция rand , реализующая равномерно распределенные числа в интервале [0; 1] .

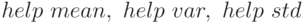Среднее значение массива чисел определяется функцией mean , дисперсия — функцией var , среднее квадратическое отклонение (стандартное отклонение) — функцией std (см. $help\mbox{ }mean,\mbox{ }help\mbox{ }var,\mbox{ }help\mbox{ }std$ ).

Программный код анализа случайных чисел:

clear, clc
%% Генерирование выборки 500 случайных чисел
x = rand(500, 1); 
%% Вычисление среднего значения выборки
m1 = mean(x)           
%% Вычисление дисперсии данной выборки
s2 = var(x)
%% Вычисление среднего квадратического отклонения 
s = std(x) 

%% Расчет относительных погрешностей в процентах
%% по математическому ожиданию
m = 0.5;
Dm = abs((mean(x)- m)/m)*100;
fprintf('\n Относительная погрешность по математическому ожиданию: %g%%\n', Dm);
%% по дисперсии
d = 1/12;
Dd = abs((var(x)- d)/d)*100;
fprintf(' Относительная погрешность по дисперсии: %g%%\n', Dd);
%% по среднему квадратическому отклонению
sd = sqrt(d);
Ds = abs((std(x)- sqrt(1/12))/sqrt(1/12))*100;

fprintf(' Относительная погрешность по стандартному отклонению: %g%%\n', Ds);

%% Генерирование дополнительной выборки
y = rand(500, 1);

%% Диаграмма оценки равномерности случайных чисел
fig1 = figure(1);
set(fig1, 'name', 'Случайные числа функции rand')
plot(x,y,'o', 'markersize', 4);
str = '\bf\fontsize{11}\fontname{times}Проверка на равномерность случайных чисел';
title(str)
xlabel('\bf\fontsize{11}\fontname{times} Random numbers')
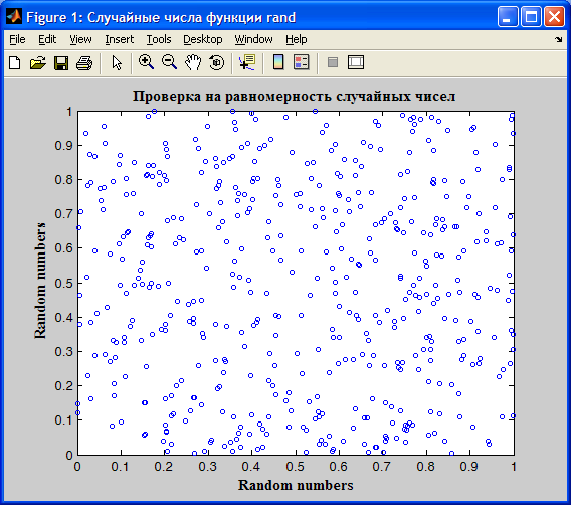
ylabel('\bf\fontsize{11}\fontname{times} Random numbers')

В программе выполняется построение диаграммы визуальной оценки равномерности случайных чисел. Числа-кружочки на диаграмме должны равномерно заполнить квадрат со стороной, равной единице. На рис. 5.1 приведен пример проверки случайной последовательности на равномерность распределения в интервале (0; 1) .

Рис. 5.1. Проверка равномерности случайных чисел для функции rand

Задание 1

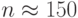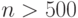Проведите в зависимости от номера компьютера статистическое исследование функции rand при различных объемах выборки: малых n < 25 ; средних $n \approx 150$ ; больших n > 500 . Результаты испытаний усредните.

Компьютер № 1: 11 испытаний (n: 24, 142, 600);
 Компьютер № 2: 12 испытаний (n: 22, 144, 650);
 Компьютер № 3: 13 испытаний (n: 20, 146, 700);
 Компьютер № 4: 14 испытаний (n: 18, 148, 750);
 Компьютер № 5: 15 испытаний (n: 16, 150, 800);
 Компьютер № 6: 16 испытаний (n: 14, 152, 850);
 Компьютер № 7: 17 испытаний (n: 12, 154, 900);
 Компьютер № 8: 18 испытаний (n: 10, 156, 950);
 Компьютер № 9: 19 испытаний (n: 19, 149,1000).
 Компьютер № 10: 20 испытаний (n: 20, 150, 1010).

Постройте график изменения относительных погрешностей среднего, дисперсии, стандартного отклонения от числа испытаний.
Пункт 1 задания выполните для выборок, сформированных в системах EXCEL, DELPHI (консольное приложение), PASCAL, С, GPSS/PC. Сформированные выборки импортируйте в MATLAB, где произведите необходимый анализ. Формирование выборки случайных чисел в GPSS/PC выполните по номеру датчика случайных чисел, который соответствует номеру компьютера ( .).
Постройте гистограммы в системе MATLAB для сформированных выборок (полученных в различных системах) с помощью графической функции (см. $help\mbox{ }hist$ ).

Примечание. В системе GPSS/PC сформируйте выборки только малых и средних объемов (в соответствии с номером компьютера).

1. Для фиксации случайных чисел в GPSS/PC можно использовать операторы 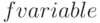fvariable , matrix и блок msavevalue .

1.2. Исследование качества ГСЧ, сформированного по методу Фибоначчи

Генератор случайных чисел, использующий метод Фибоначчи, применялся в начале 50-х годов ХХ века [9]. Рекуррентное соотношение Фибонначи имеет вид

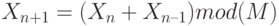$X_{n+1} = (X_{n} + X_{n–1}) mod(M)$ ,

где:

$X_{n+1}, X_{n}, X_{n–1}$ — целые числа, лежащие между нулем и некоторым большим числом , который называется модулем;

— порядковый номер числа [9].

Для получения случайных чисел 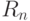$R_{n}$ из интервала [0; 1] следует вычислить дробь

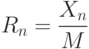
$R_n=\frac{X_n}{M}$

Программный код формирования случайных чисел по методу Фибоначчи:

clear,clc,close all
 
N = 500;  %% количество генерируемых чисел
M = 2^30; %% модуль
 
%% 1-я последовательность случайных чисел
X0 = 12345; %% 1-е произвольное число
X1 = 67890; %% 2-е произвольное число

for n = 1 : N 

X = mod( X1 + X0, M); %% следующее число
X0 = X1;
X1 = X;
Zx(n,1) = X;

end
Rx = Zx/M;
 
mf = mean(Rx);
fprintf('\n Среднее выборочное для метода Фибоначчи: %g%%\n', mf);
 
sf2 = var(Rx);
fprintf(' Выборочная дисперсия для метода Фибоначчи: %g%%\n', sf2);
 
sf = std(Rx);
fprintf(' Выборочное стандартное отклонение: %g%%\n', sf);
 
%% Расчет относительных погрешностей в процентах
m = 0.5;
fprintf('\n Относительная погрешность по математическому ожиданию: %g%%\n', abs((mf - m)/m)*100);

d = 1/12;
fprintf(' Относительная погрешность по дисперсии: %g%%\n', abs((sf2 - d)/d)*100);

%% по среднему квадратическому отклонению
sd = sqrt(d);
fprintf(' Относительная погрешность по стандартному отклонению: %g%%\n', abs((sf - sd)/sd)*100);
 

%% 2-я последовательность случайных чисел
Y0 = 333; %% 1-е произвольное число
Y1 = 123; %% 1-е произвольное число

for n = 1 : N 

Y = mod( Y1 + Y0, M); %% следующее число
Y0 = Y1;
Y1 = Y;
Zy(n,1) = Y;

end

Ry = Zy/M;

%% Диаграмма оценки равномерности случайных чисел
fig2 = figure(2);
set(fig2, 'name', 'Случайные числа Фибоначчи')
plot(Rx,Ry,'o', 'markersize', 4);
str = '\bf\fontsize{11}\fontname{times}Проверка на равномерность случайных чисел';
title(str)
xlabel('\bf\fontsize{11}\fontname{times} Random numbers')
ylabel('\bf\fontsize{11}\fontname{times} Random numbers')

Пример выполнения программы (без диаграммы)

Среднее выборочное для метода Фибоначчи: 0.49687%
 Выборочная дисперсия для метода Фибоначчи: 0.0861675%
 Выборочное стандартное отклонение: 0.293543%

 Относительная погрешность по математическому ожиданию: 0.626048%
 Относительная погрешность по дисперсии: 3.40103%
 Относительная погрешность по стандартному отклонению: 1.6863%

Задание 2

Напишите программу формирования простых трехзначных чисел с целью их использования в качестве начальных чисел в методе Фибоначчи. Рассчитайте относительные погрешности по математическому ожиданию, дисперсии, стандартному отклонению.
Напишите программу формирования случайных чисел Фибоначчи без вспомогательных массивов 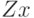и .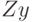
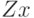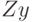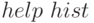Постройте гистограммы в системе MATLAB для сформированных выборок ( и ) с помощью графической функции (см. $help\mbox{ }hist$ ) с разбивкой графического окна с помощью функции 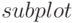(см. $help\mbox{ }subplot$ ).

1.3. Исследование качества ГСЧ, сформированного по методу срединных квадратов

Метод срединных квадратов был предложен Нейманом [19] и заключается в следующем: выбирается число, меньшее 1, разрядностью . Оно возводится в квадрат. Из полученного результата (разрядность которого должна быть 2*(2n) , если нет, то добавляются нули справа от полученного числа) выбираются чисел из середины полученного после возведения в квадрат числа. Число записывается после десятичной точки. Далее все повторяется.

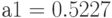Для примера выберем 4-разрядное ( 2n = 4 ) число а0 = 0.1234 . После возведения в квадрат получим число, равное 0.01522756. Из него выбираем четыре срединные цифры, т. е. 5227. Получаем новое случайное (псевдослучайное) число а1 = 0.5227 . Описанные действия отобразим в следующем виде:

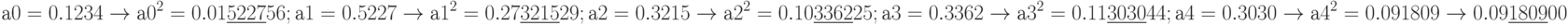
$а0 = 0.1234 \to а0^2=0.01\underline{5227}56;\\ а1 = 0.5227 \to а1^2=0.27\underline{3215}29;\\ а2 = 0.3215 \to а2^2=0.10\underline{3362}25;\\ а3 = 0.3362 \to а3^2=0.11\underline{3030}44;\\ а4 = 0.3030 \to а4^2=0.091809 \to 0.09\underline{1809}00$

и так далее.

Задание 3

Напишите программу формирования случайных чисел по методу срединных.
Начальное число выберите (по указанию преподавателя) из следующего списка, приведенного в таблице 5.1.

Таблица 5.1.
Варианты заданий для метода срединных квадратов
№ 1	; ; ; ; ; ; ; ; ;
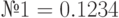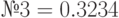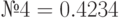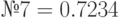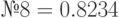№ 2	; ; ; ; ; ; ; ; ;
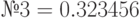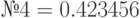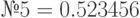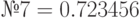№ 3	; ; ; ; ; ; ; ; ;
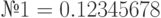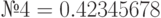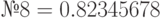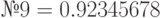№ 4	; ; ; ; ; ; ; ; ;

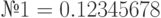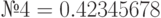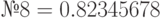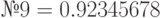Примечание. Для проверки периодичности (непериодичности) формируемой случайной последовательности можно применить, например, функцию unique (см. $help\mbox{ }unique$ ).

Проведите, в зависимости от номера компьютера, статистическое исследование ГСЧ (вычисление среднего значения выборки, дисперсии, стандартного отклонения выборки) при различных объемах выборки: малых n < 25

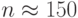, средних $n \approx 150$ , больших n > 500

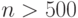. Результаты испытаний усредните и сравните с аналогичными результатами, которые проведены для выборки, сформированной с помощью функции rand системы MATLAB.

Компьютер № 1: (объем выборки: 24, 142, 600);
 Компьютер № 2: (объем выборки: 22, 144, 650);
 Компьютер № 3: (объем выборки: 20, 146, 700);
 Компьютер № 4: (объем выборки: 18, 148, 750);
 Компьютер № 5: (объем выборки: 16, 150, 800);
 Компьютер № 6: (объем выборки: 14, 152, 850);
 Компьютер № 7: (объем выборки: 12, 154, 900);
 Компьютер № 8: (объем выборки: 10, 156, 950);
 Компьютер № 9: (объем выборки: 17, 157, 999);
 Компьютер № 10: (объем выборки: 19, 158, 1010).

Постройте в системе MATLAB гистограммы для сформированных выборок случайных чисел по методу срединных квадратов и сравните с гистограммой для выборок, сформированных с помощью функции системы MATLAB.
Постройте гистограммы для сформированных выборок.
Постройте диаграмму визуального контроля равномерного заполнения квадрата со стороной, равной единице.

Дальше >>

Авторизоваться

Моделирование систем

Исследование качества генераторов случайных чисел