НОУ ИНТУИТ | Моделирование систем. Лекция 10: Планирование активного эксперимента при поиске оптимальных условий

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

Мордовский государственный университет имени Н.П. Огарева

Опубликован: 30.11.2010 | Доступ: свободный | Студентов: 3296 / 1995 | Оценка: 4.12 / 4.13 | Длительность: 14:37:00

ISBN: 978-5-9963-0352-6

Темы: Программирование, Алгоритмы и дискретные структуры

Специальности: Программист, Системный архитектор

|

Вам нравится? Нравится 32 студентам

| Поделиться |

Поддержать курс

| Скачать электронную книгу

Аннотация: Цель работы: изучить методику планирования активного эксперимента при поиске экстремума функции отклика как функции двух переменных — факторов. Среда программирования — MATLAB.

Ключевые слова: экстремум функции, поиск, факторное пространство, экстремум, функция, градиентный метод, градиент функции, линейная модель, активный эксперимент, коэффициенты

Теоретическая часть

Одной из центральных задач планирования эксперимента является задача поиска экстремума функции отклика [1] — например, при оптимизации производственных и других процессов.

Поиск экстремума функции отклика происходит путем исследования поверхности отклика. Это исследование осуществляется посредством измерения поверхности отклика в различных точках факторного пространства. Возникает вопрос: какой должна быть стратегия планирования эксперимента, чтобы число опытов (измерений), необходимое для нахождения экстремума или близких к нему значений, было как можно меньше?

Воспользоваться с этой целью непосредственно известными методами поиска экстремума функции многих переменных невозможно, поскольку "измерение" функции отклика в каждой точке факторного пространства происходит с ошибкой. Однако эти методы составляют основу методов поиска экстремума функции отклика.

При решении задач планирования эксперимента наибольшее распространение получили алгоритмы поиска, использующие градиентные методы. Их особенность состоит в том, что движение при поиске происходит в направлении не самого градиента, который неизвестен, а его оценки. Если функция отклика априорно выражается зависимостью 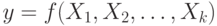$y = f(X_{1}, X_{2}, … , X_{k})$ , то оценка градиента 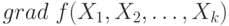$grad\mbox{ }f(X_{1}, X_{2}, … , X_{k})$ в точке факторного пространства при этом находится по результатам измерений, проводимым в ее окрестности. Из класса градиентных методов практическое применение получил метод, разработанный Боксом и Уильсоном. В нем используется метод крутого восхождения в сочетании с последовательно планируемым факторным экспериментом для нахождения оценки градиента [1]. В общем виде метод Бокса и Уильсона состоит в следующем:

построение факторного эксперимента в окрестности некоторой точки;
вычисление оценки градиента в этой точке по результатам эксперимента;
крутое восхождение в направлении оценки градиента;
нахождение оценки максимума (минимума) функции отклика по этому направлению;
анализ оценки максимума функции отклика и принятие решения о дальнейшем восхождении.

1. Оценивание градиента

Рассмотрим оценивание градиента функции отклика, когда факторы имеют два уровня. Пусть функция отклика

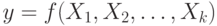( 10.1)

определена в области 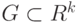$G\subset R^k$ .

Используем произвольную точку факторного пространства 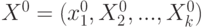X^0=(x_1^0,X_2^0,...,X_k^0) как центр плана. Верхний 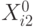$X_{i2}^0$ и нижний 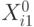$X_{i1}^0$ уровни выбираем симметричными относительно центра плана, чтобы перейти к кодированным переменным (факторам):

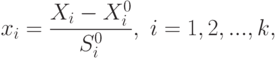
$x_i=\frac{X_i-X_i^0}{S_i^0},\mbox{ }i=1,2,...,k,$

где 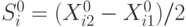$S_i^0=(X_{i2}^0-X_{i1}^0)/2$ — интервал варьирования.

Тогда функцию отклика (10.1) можно выразить через кодированные переменные:

( 10.2)

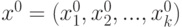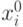
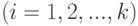Под задачей оценивания градиента теперь понимается определение оценки градиента функции отклика (10.2) в точке x^0=(x_1^0,x_2^0,...,x_k^0) , где x_i^0 (i=1,2,...,k) , т. е. в нулевой точке кодированных переменных. Принимаем, что в окрестности точки 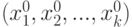функция отклика (10.2) допускает разложение по формуле Тейлора вида

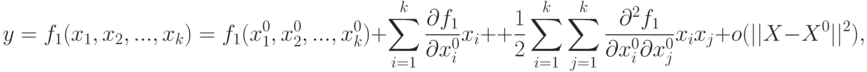$y=f_1(x_1,x_2,...,x_k)=f_1(x_1^0,x_2^0,...,x_k^0)+\sum\limits_{i=1}^{k}\frac{\partial f_1}{\partial x_i^0}x_i+\\ +\frac{1}{2}\sum\limits_{i=1}^{k}\sum\limits_{j=1}^{k}\frac{\partial^2 f_1}{\partial x_i^0\partial x_j^0}x_ix_j+ o(|| X-X^0||^2),$

( 10.3)

где $\lim\limits_{x\to x^0} o(|| X-X^0||^2)=0$ .

Как известно [10], вектор-градиент функции 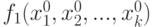f_1(x_1^0,x_2^0,...,x_k^0) в заданной точке 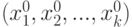есть

$grad\mbox{ }f_1(x_1^0,x_2^0,...,x_k^0)= \left( \begin{array}{c} \frac{\partial f_1}{\partial x_1^0} \\ \frac{\partial f_1}{\partial x_2^0}\\ \vdots\\ \frac{\partial f_1}{\partial x_k^0} \end{array} \right) = \left( \frac{\partial f_1}{\partial x_i^0}, \frac{\partial f_1}{\partial x_i^0}, ..., \frac{\partial f_1}{\partial x_i^0} \right)^T.$

( 10.4)

Частные производные в (10.3) и в (10.4) рассчитываются в заданных точках и, таким образом, они представляют собой числовые значения.

Используем обозначения

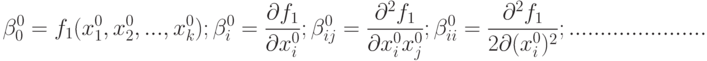$\beta_0^0=f_1(x_1^0,x_2^0,...,x_k^0);\\ \beta_i^0=\frac{\partial f_1}{\partial x_i^0};\\ \beta_{ij}^0=\frac{\partial^2 f_1}{\partial x_i^0x_j^0};\\ \beta_{ii}^0=\frac{\partial^2 f_1}{2\partial (x_i^0)^2};\\ ......................\\$

( 10.5)

С учетом введенных обозначений (10.5) можно записать, что функция отклика будет определяться в следующем виде:

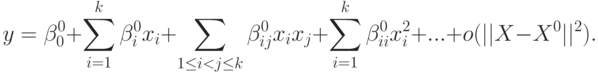$y=\beta_0^0+ \sum\limits_{i=1}^{k}\beta_i^0x_i+ \sum\limits_{1\le i<j\le k}^{}\beta_{ij}^0x_ix_j+ \sum\limits_{i=1}^{k}\beta_{ii}^0x_i^2+...+o(|| X-X^0||^2).$

( 10.6)

Отметим также, что

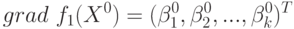
$grad\mbox{ }f_1(X^0)=(\beta_1^0,\beta_2^0,...,\beta_k^0)^T$

Разложение (10.6) можно рассматривать как многофакторное уравнение регрессии, линейное относительно своих коэффициентов.

Таким образом, для оценки градиента — оценки коэффициентов уравнения регрессии 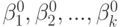$\beta_1^0,\beta_2^0,...,\beta_k^0$ можно использовать метод наименьших квадратов, с помощью которого возможно определить все коэффициенты аппроксимации поверхности отклика и затем выделить оценки коэффициентов 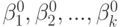$\beta_1^0,\beta_2^0,...,\beta_k^0$ , оценку градиента. Вид аппроксимации, количество слагаемых в разложении (10.6) задает исследователь по своим априорным сведениям.

2. Метод Бокса и Уильсона

Пусть функция отклика относительно кодированных переменных имеет вид

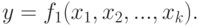( 10.7)

Для функции отклика (10.7) может быть найдена оценка градиента в точке 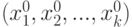(x_1^0,x_2^0,...,x_k^0) .

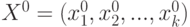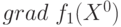Для поиска максимума функции отклика делается некоторый шаг (первый шаг) из точки X^0=(x_1^0,x_2^0,...,x_k^0) в направлении оценки градиента $grad\mbox{ }f_1(X^0)$ :

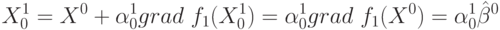$X_0^1=X^0+\alpha_0^1 grad\mbox{ }f_1(X^1_0)=\alpha_0^1 grad\mbox{ }f_1(X^0)=\alpha_0^1 \hat\beta^0$

( 10.8)

где:

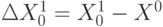$\alpha_0^1 >0$ — скаляр, параметр шага $\Delta X_0^1=X_0^1-X^0$ ;

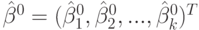$\hat\beta^0=(\hat\beta^0_1,\hat\beta^0_2,...,\hat\beta^0_k)^T$ — оценка градиента на предыдущем шаге;

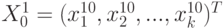$X^1_0=(x_1^{10},x_2^{10},...,x_k^{10})^T$ — новая точка факторного пространства.

Векторная запись (10.8) в координатной форме имеет вид

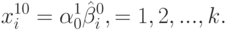$x_i^{10}=\alpha_0^1 \hat\beta_i^0,\qquadi=1,2,...,k.$

( 10.9)

Переход от кодированных переменных $x_i^{10}$ к натуральным переменным $X_i^{10}$ осуществляется по формуле

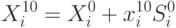$X_i^{10}=X_i^{0}+x_i^{10}S_i^{0}$

( 10.10)

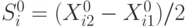где $S_i^{0}=(X_{i2}^{0}-X_{i1}^{0})/2$ .

В точке кодированных переменных (факторов) 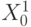$X_{0}^{1}$ следует произвести наблюдения функции отклика 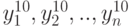$y_1^{10},y_2^{10},..,y_n^{10}$ и найти ее оценку:

$\hat y_0^1=\frac{1}{n}\sum\limits_{u=1}^{n}y_u^{10}.$

( 10.11)

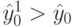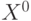Оценка функции отклика (10.11) есть результат измерений, которые производятся в реальных условиях с ошибками. Так как задача заключается в определении максимума функции отклика, естественно предположить, что оценка (10.11) значимо больше оценки в начальной точке, т. е. $\hat y_0^1 >\hat y_0$ , где $\hat y_0$ — оценка функции отклика в точке факторного пространства X^0 . Тогда можно сделать следующий шаг в направлении градиента (его оценки) 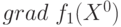$grad\mbox{ }f_1(X^0)$ . Записывая (10.8) для -го шага, будем иметь точку факторного пространства, полученную в направлении оценки градиента, т. е.

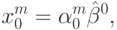$x_0^m=\alpha_0^m\hat \beta^0,$

( 10.12)

где $\alpha_0^m >\alpha_0^{m-1}>...>\alpha_0^1$ .

Для каждого шага рассчитывается оценка функции отклика для всех точек плана. Например, для двухфакторного полного эксперимента потребуется четыре измерения функции отклика. для трехфакторного эксперимента — восемь измерений и т. д.

В направлении градиента производится средняя оценка функции отклика для значений $\alpha_0^m >\alpha_0^{m-1}>...>\alpha_0^1$ параметров шага. Как только будет найдена максимальная оценка функции отклика, то ее и принимают за оценку максимума функции отклика при движении в направлении оценки градиента [1]. Определение максимума функции отклика осуществляется простым перебором и сравнением, что, однако, приводит к увеличению затрат на проведение эксперимента.

После определения максимума оценки функции отклика производится переход к системе координат натуральных факторов (переход от кодированных к натуральным). Относительно точки, в которой найдена оценка максимума функции отклика, строится новый факторный план со своими интервалами варьирования факторов. Снова вводятся кодированные переменные и производится расчет параметров линейной модели — коэффициентов уравнения регрессии. Определяются оценки составляющих градиента в новой точке планирования. Далее делаются шаги в направлении градиента, чтобы найти оценку максимума функции отклика.

Таким образом, организуется крутое восхождение к экстремуму функции отклика. В этом состоит схематичное изложение метода Бокса и Уильсона. Следует иметь в виду, что аналитический вид функции отклика, как правило, неизвестен.

В заключение следует отметить, что при планировании основная задача состоит в повышении эффективности эксперимента. Если эксперимент в реальных условиях является дорогостоящим, то поиск часто заканчивают при получении удовлетворительных для исследователя значений функции отклика без достижения области экстремума. Достижение области экстремума в этом случае по экономическим соображениям может оказаться нецелесообразным.

Дальше >>

Авторизоваться

Моделирование систем

Планирование активного эксперимента при поиске оптимальных условий

Теоретическая часть

1. Оценивание градиента

2. Метод Бокса и Уильсона

Вопросы и ответы