НОУ ИНТУИТ | Моделирование систем. Лекция 3: Моделирование непрерывных случайных величин с заданным законом распределения

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

Мордовский государственный университет имени Н.П. Огарева

Опубликован: 30.11.2010 | Доступ: свободный | Студентов: 3296 / 1995 | Оценка: 4.12 / 4.13 | Длительность: 14:37:00

ISBN: 978-5-9963-0352-6

Темы: Программирование, Алгоритмы и дискретные структуры

Специальности: Программист, Системный архитектор

|

Вам нравится? Нравится 32 студентам

| Поделиться |

Поддержать курс

| Скачать электронную книгу

Аннотация: Цель работы: изучить и освоить методы моделирования случайных величин, распределенных по таким часто применяемым законам распределения в системах массового обслуживания, как равномерный, экспоненциальный, нормальный, распределение Эрланга, с целью программной реализации алгоритмов формирования случайных величин с заданным законом распределения. Моделирование осуществляется в программных средах MATLAB и GPSS/PC.

Ключевые слова: функция, график функции, значение, вероятность, случайная величина, выражение, нормальное распределение, дискретное распределение, эмпирическая функция, нормальный закон, стандартное отклонение, GPSS, числовая ось

Теоретическая часть

Во многих программных средах имеются генераторы случайных (псевдослучайных) чисел, которые обеспечивают формирование случайных чисел, равномерно распределенных в интервале [0; 1] . На основе этого распределения могут быть сформированы выборки случайных чисел с каким-либо другим законом распределения случайной величины. В некоторых случаях этого можно добиться на основе метода инверсии, или метода обратной функции. Суть метода обратной функции заключается в следующем. 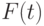Пусть есть некоторая функция распределения F(t) случайной величины , которая по определению является неотрицательной и не превосходящей значения 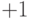. Если выбрать на оси ординат графика функции 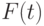F(t) случайную точку , то мы сможем получить значение величины такое, что F(t) = r . 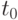Как известно, функция распределения есть вероятность того, что случайная величина t_0 не превысит своего некоторого значения , т. е. F(t) = P(t_0 < t) . 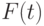На основе заданной функции распределения F(t) существует однозначное соответствие между значением аргумента функции и значением самой функции, что позволяет записать выражение F(t) = P(t0 < t) = P(R < F(t)) , где — случайная величина, равномерно распределенная в интервале [0; 1] . Используя соотношение f(t) = dF(t)/dt , можно записать функцию распределения случайной величины :

$F(t)=P(t_{0} < t)=\int\limits_{0}^{t} f(\tau)d\tau =P(R<F(t))=\int\limits_{0}^{F(t)} f(r)dr.$

( 3.1)

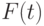Таким образом, последовательность случайных чисел r_1, r_2, … , принадлежащая интервалу [0; 1] , преобразуется в последовательность t_1, t_2, … , которая имеет заданную функцию распределения F(t) и, соответственно, функцию плотности f(t) .

Метод обратной функции нельзя применять напрямую к непрерывным распределениям, для которых функция распределения не может быть выражена в квадратурах от соответствующей функции плотности. Типичными примерами такого рода являются нормальное распределение, гамма-распределение, логарифмически-нормальное распределение, а также дискретное распределение Пуассона. В таких случаях для получения выборок случайных чисел можно воспользоваться одним из следующих методов:

аппроксимацией непрерывной функции 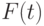дискретной функцией распределения;
получением с помощью статистических соотношений необходимой информации на основе других распределений, имеющих простую аналитическую форму.

Например, в случае второго метода, случайная величина, подчиняющаяся распределению Эрланга -го порядка (или гамма-распределению с целочисленным параметром), представляет собой сумму экспоненциально распределенных случайных величин, а время между наступлениями событий в пуассоновском процессе также распределено экспоненциально.

Практическая часть

1. Формирование выборки случайных чисел с равномерным распределением в заданном интервале

Равномерно распределенная случайная величина в интервале [a; b] имеет функцию плотности

$f(t)=\frac{1}{b-a}.$

Определим функцию распределения в соответствии с (1.1) и приравняем случайному числу , равномерно распределенному в интервале [0; 1] :

$F(t)=R=\int\limits_{a}^{t} \frac{d\tau}{b-a}=\left.\frac{\tau}{b-a}\right|_{a}^{t}=\frac{t}{b-a}-\frac{a}{b-a}=\frac{t-a}{b-a};\Rightarrow t=a+(b-a)R.$

( 3.2)

Если требуется сформировать выборку из случайных чисел из интервала [a; b] , то выражение (3.2) перепишем в виде

$t_{i}=a+(b-a)R_{i},\mbox{ }i=\overline{1,N}.$

( 3.3)

В системе MATLAB случайные числа, равномерно распределенные в интервале [0; 1] , формируются встроенной функцией rand (см. help rand ).

Рассмотрим следующий пример формирования выборки случайных чисел в системе MATLAB.

Пример 1. Сформируйте 20 случайных чисел с равномерным распределением из интервала [2; 5] .

Программный код решения примера (возможно, в командном окне MATLAB):

a = 2; b = 5; N = 20;
t20 = a + (b - a)*rand(N,1)

Задание 1

Рассчитайте теоретическое значение математического ожидания случайной величины, равномерно распределенной в интервале . Рассчитайте среднее значение величины при трехкратном обращении к программе. Сравните результаты.
Постройте функцию распределения случайной величины из интервала по сформированной выборке. Интервал примите следующим (в соответствии с номером компьютера, за которым выполняется лабораторная работа):
```
№1: [–1; 1.1]; №2: [–0.2; 2.2]; №3: [–3; 3.3]; №4: [–4.4; 6.6];  №5: [–5, 5.5]; 
№6: [–6.6, –3.3]; №7: [–7, 8]; №8: [–8, 8.8]; №9: [–9, 9]; №10: [–10.1, 10.1].
```

2. Формирование выборки случайных чисел с экспоненциальным распределением

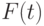Функция плотности f(t) экспоненциального распределения случайной величины и функция распределения F(t) даются формулами

$f(t)=\lambda e^{-\lambda t},\qquad F(t)=1-e^{-\lambda t},$

где $\lambda$ — параметр экспоненциального распределения, имеющий размерность $с^{-1}$ .

В соответствии с методом обратной функции запишем откуда найдем :

$t=-\frac{1}{\lambda}\ell n (1-R).$

( 3.4)

Известно, что функция случайной величины имеет такое же распределение, что и сама случайная величина . Поэтому (3.4) представим в виде

$t_{i}=-\frac{1}{\lambda}\ell n (R_{i}),\qquad i=\overline{1,N}.$

( 3.5)

Рассмотрим пример формирования выборки случайных чисел с экспоненциальным распределением в MATLAB.

Пример 2. Сформируйте N = 20 случайных чисел с экспоненциальным распределением по методу обратной функции.

Программный код решения примера:

L = 0.25; N = 20;
texp20 = -1/L*log(rand(N,1))

Если воспользоваться встроенной функцией exprnd (см. help exprnd ) системы MATLAB, то будем иметь следующий программный код:

L = 0.25; N = 20;
texp20M = exprnd(1/L,N,1)

Следует обратить внимание, что аргументом функции exprnd является величина математического ожидания ( $М = 1/\lambda$ ) экспоненциального распределения.

Для приведенных программ результаты их выполнения не приводятся, так как они будут различными при каждом выполнении программы.

В системе MATLAB эмпирическую функцию распределения можно построить с помощью cdfplot (см. help cdfplot ). Тогда программа формирования и построения функции распределения примет следующий вид:

clear,clc
L = 0.25; N = 20;
texp20  = –1/L*log(rand(N,1));
cdfplot(texp20), %% специальная графическая функция
title('\bf  Функция экспоненциального распределения');
xlabel('\bf - - - - - - - t - - - - - - - ');
ylabel('\bf F(t)');

Примечание. Моделирование случайной величины с экспоненциальным распределением и заданным параметром можно произвести, взяв за основу моделирование случайной величины с экспоненциальным распределением и параметром, равным единице [21]. В этом случае поступают следующим образом:

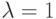генерируют значения случайной величины, распределенной по экспоненциальному закону с параметром $\lambda = 1$ ;
находят произведение полученного значения и математического ожидания случайной величины, у которой $\lambda \ne 1$ . Математическое ожидание экспоненциально распределенной величины обратно пропорционально параметру.

Задание 2

Постройте эмпирическую функцию плотности экспоненциального распределения по сформированному массиву случайных чисел.
Постройте эмпирическую функцию распределения по сформированному массиву случайных чисел без применения функции .
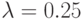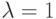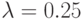Сравните выборку случайных чисел, распределенных по экспоненциальному закону с параметром $\lambda = 0.25$ , и выборку чисел, полученных для $\lambda = 1$ , с последующим преобразованием — умножением математического ожидания на массив сформированных чисел, для которых $\lambda = 0.25$ .
Сформируйте выборку случайных чисел с экспоненциальным распределением по формуле (3.5) с помощью операторов цикла.

Дальше >>

Авторизоваться

Моделирование систем

Моделирование непрерывных случайных величин с заданным законом распределения

Теоретическая часть

Практическая часть

1. Формирование выборки случайных чисел с равномерным распределением в заданном интервале

2. Формирование выборки случайных чисел с экспоненциальным распределением

Вопросы и ответы