Моделирование непрерывных случайных величин с заданным законом распределения

6. Формирование выборки случайных чисел, распределенных по закону эрланга k-го порядка

Случайная величина, подчиняющаяся распределению Эрланга с параметрами (порядок распределения Эрланга) и , представляет собой сумму n независимых, одинаково распределенных случайных величин с параметром (интенсивность, ) [20]. Это означает, что можно получить выборку, соответствующую распределению Эрланга, при помощи многократного применения метода инверсии (метода обратной функции).

Пример 6. Сформируйте выборку объема случайных чисел с распределением Эрланга 3-го порядка ( ) и параметром .

Программный код решения примера:

L = 1.25; k = 3;
N = 1000;
for I = 1 : N
    T(I) = 0;
    for J = 1 : k
    T(I) = T(I) - 1/L*log(rand);
end
end
T2 = sort(T);

Задание 6

1. Упростите программный код, используя матричные возможности системы MATLAB.
2. Постройте функцию плотности и функцию распределения по аналитическим формулам для распределения Эрланга [3]:
   
3. Выполните предыдущий пункт с помощью встроенных функций и . Сравнить результаты.

7. Моделирование процесса обслуживания по закону эрланга k-го порядка в системе GPSS/PC

Для моделирования распределения Эрланга -го порядка используется экспоненциальная функция распределения, которая может оставаться неизменной при изменении порядка потока Эрланга.

Пример 7. Смоделируйте одноканальную систему массового обслуживания, в которую требования поступают по равномерному закону через мин., а обслуживание осуществляется по закону Эрланга 3-го порядка с параметром \ . Произведите обслуживание 5600 требований.

Для решения примера 7 сначала сформируем функцию экспоненциального распределения случайной величины с параметром 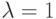, а затем выполним пересчет для параметра 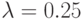. Для этого может быть использована следующая программа в системе MATLAB:

clear, clc
L = 0.25; 
t = linspace(0, 9, 50);
F = 1 - exp(-t);
t2 = 1/L*t;
fid = fopen('erlang.txt', 'w'); %% запись в текстовый файл
fprintf(fid, '\nexp function RN22,C50\n');
for J = 1 : length(F)
if mod(J,3)
fprintf(fid, '%g,%g/', F(J), t2(J));
    
else
fprintf(fid, '\r\n');
fprintf(fid, '%g,%g/', F(J), t2(J));
end
end
fprintf(fid,'\r\n;------------------------------\r\n');
fclose(fid);

Программный код решения примера в системе GPSS/PC:

simulate
exp function RN22,C50
0,0/0.167792,0.734694/

0.307431,1.46939/0.423639,2.20408/0.520348,2.93878/
0.60083,3.67347/0.667808,4.40816/0.723547,5.14286/
0.769934,5.87755/0.808537,6.61224/0.840663,7.34694/
0.867399,8.08163/0.889648,8.81633/0.908164,9.55102/
0.923574,10.2857/0.936397,11.0204/0.947069,11.7551/
0.955951,12.4898/0.963342,13.2245/0.969493,13.9592/
0.974612,14.6939/0.978872,15.4286/0.982417,16.1633/
0.985367,16.898/0.987822,17.6327/0.989866,18.3673/
0.991566,19.102/0.992981,19.8367/0.994159,20.5714/
0.995139,21.3061/0.995955,22.0408/0.996633,22.7755/
0.997198,23.5102/0.997668,24.2449/0.99806,24.9796/
0.998385,25.7143/0.998656,26.449/0.998882,27.1837/
0.999069,27.9184/0.999225,28.6531/0.999355,29.3878/
0.999464,30.1224/0.999554,30.8571/0.999628,31.5918/
0.999691,32.3265/0.999743,33.0612/0.999786,33.7959/
0.999822,34.5306/0.999852,35.2653/0.999877,36/
;------------------------------
tab1 table mp1,0,3,50
******** Erlang distribution *******
10  generate 18,2
20  assign 1,1
30  seize 1
40  mark 1
50  advance 1,fn$exp
60  advance 1,fn$exp
70  advance 1,fn$exp
80  tabulate tab1
90  release 1
100  terminate 1
start 5600
;end

В программе обслуживание по закону Эрланга 3-го порядка осуществляется с помощью трехкратной временной задержки транзактов на время, распределенное по экспоненциальному закону с заданным параметром. Временная задержка производится блоками (строки 50, 60, 70). Контролируемая отметка времени осуществляется блоком по 1-му параметру и табулированием стандартного числового атрибута с помощью оператора (с меткой tab1). Таким образом, реализация обслуживания транзактов (требований) по закону Эрланга -го порядка может быть запрограммирована с помощью блоков в теле устройства, т. е. между блоками и . Результат выполнения программы показан на рис. 3.2, который дает наглядное представление о форме распределения времени обслуживания, и в нем приводятся числовые данные распределения – среднее значение, равное 10.72, и стандартное отклонение, равное 6.92.

Рис. 3.2. Распределение времени обслуживания по закону Эрланга

Рассчитаем величину параметра закона Эрланга 3-го порядка по данным рис. 2 или из файла стандартного отчета. Как известно [2], математическое ожидание и параметр закона Эрланга -го порядка связаны между собой формулой

или

Применим первую формулу, считая, что среднее равно 10.72:

Получен результат одного порядка по сравнению с заданным условием.

Задание 7

1. По файлу стандартного отчета постройте в MATLAB функцию распределения времени обслуживания транзактов в устройстве.
2. В соответствии с номером компьютера, за которым выполняется лабораторная работа, примите следующие числа обработки транзактов (оператор 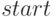): № 1: 1000; № 2: 2000 и т. д. Проанализируйте результаты, рассчитайте параметр закона Эрланга 3-го порядка.

Контрольные вопросы

1. Что из себя представляет график функции плотности равномерного закона распределения случайных величин?
2. Как формируется поток Эрланга -го порядка?
3. Чему соответствует область определения функции распределения случайных величин экспоненциального закона?
4. Чему соответствует область определения функции распределения случайных величин равномерного закона?
5. Какая связь между стандартным отклонением и дисперсией случайных величин?
6. Что собой отображает гистограмма случайных величин?
7. Какая связь между функцией плотности и функцией распределения случайных непрерывных величин?
8. Что является параметром в экспоненциальном законе распределения случайных величин? Какой функциональный смысл имеет параметр экспоненциального распределения случайной величины?
9. Назовите допустимую область определения функции распределения потока Эрланга -го порядка.