|
Добрый день. Я приступила сегодня к самостоятельному изучению курса "Моделирование систем". Хочу понять - необходимо ли отсылать мои решения практических заданий на сайт, (и если да - то где найти волшебную кнопку "Загрузить...") или практические задания остаются полностью на моей совести? (никто не проверяет, и отчётности по ним я предоставлять не обязана?) P.S.: тьютора я не брала |
Моделирование многофазных систем массового обслуживания
Теоретическая часть
Анализ многофазных систем массового обслуживания основан на теоретическом материале, взятом из [20].
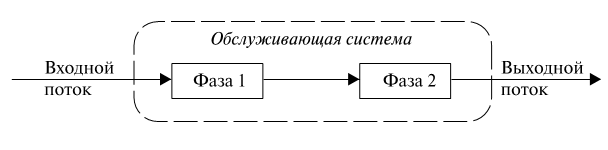
Система массового обслуживания может представляться в виде много-фазной модели, когда каждое требование в ней последовательно обслуживается во всех фазах (приборах обслуживания). При этом если очереди перед каждой фазой не допускаются, то система будет называться системой с нулевой вместимостью блоков ожидания [20].
Работа двухфазной системы обслуживания состоит в следующем. Каждая фаза может быть занята на обслуживание либо свободна. Поскольку перед фазой очередь не допускается, то принимается, что первая фаза обслуживания заблокирована, если обслуживание требования в данной (первой) фазе завершено, а вторая фаза не готова к приему требования по той причине, что в ней не закончено обслуживание. Принимается также, что если первая фаза занята, то очередное входящее требование получает отказ. В системе могут быть следующие состояния: "фаза свободна", "фаза занята", "фаза заблокирована", которые обозначают как  ,
,  ,
,  соответственно.
соответственно.
1. Двухфазная система обслуживания
Схема двухфазной системы обслуживания показана на рис. 1.1.
Если состояние первой фазы обозначить символом  , а состояние второй фазы — символом
, а состояние второй фазы — символом  , то множество состояний двухфазной системы обслуживания будет следующим:
, то множество состояний двухфазной системы обслуживания будет следующим:
 |
( 1.1) |
Примем, что входной поток требований имеет пуассоновское распределение, а обслуживание в фазах осуществляется по экспоненциальному вероятностному закону. Рассматривая вероятности переходов из одного состояния в другое во времени, можно получить следующие дифференциальные уравнения относительно вероятностей состояний 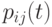 двухфазной системы:
двухфазной системы:
 |
( 1.2) |
Система (1.2) — это система однородных обыкновенных дифференциальных уравнений с постоянными коэффициентами. Ее можно представить в матричном виде:
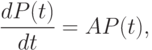
где:
 — вектор размера
— вектор размера  с элементами
с элементами  ,
, 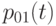 ,
,  ,
, 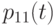 ,
, 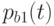 ;
;
 — матрица коэффициентов размера
— матрица коэффициентов размера  , которая имеет следующий вид:
, которая имеет следующий вид:
![A=
\left[ \begin{array}{ccccc}
-\lambda & \mu & 0 & 0 & 0 \\
0 & -(\mu+\lambda) & \mu & 0 & \mu \\
\lambda & 0 & -\mu & \mu & 0 \\
0 & \lambda & 0 & -2\mu & 0 \\
0 & 0 & 0 & \mu & -\mu \\
\end{array} \right]](/sites/default/files/tex_cache/8b0b443ac2934908ea804ec30f8c5b22.png)
Для интегрирования системы (1.2) будем задавать естественные начальные условия, т. е. такие, когда в начальный момент времени, равный нулю, вероятность отсутствия требований в системе равна единице, а остальные вероятности в начальный момент времени равны нулю:
 |
( 1.3) |
2. Трехфазная система обслуживания
В трехфазной системе каждая из фаз может быть свободной (символ  ) либо занятой (символ
) либо занятой (символ  ), а фазы 1 и 2 могут быть к тому же заблокированы (символ
), а фазы 1 и 2 могут быть к тому же заблокированы (символ  ). Если состояние первой фазы обозначить символом
). Если состояние первой фазы обозначить символом  , состояние второй фазы — символом
, состояние второй фазы — символом  , а состояние третьей фазы — символом
, а состояние третьей фазы — символом  , то возможные состояния трехфазной системы будут следующими:
, то возможные состояния трехфазной системы будут следующими:
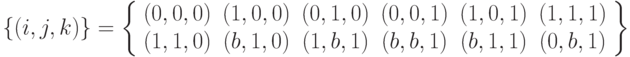 |
( 1.4) |
В соответствии с возможными состояниями (1.4) трехфазной системы можно получить следующую систему дифференциальных уравнений 13-го порядка относительно вероятностей состояний  :
:
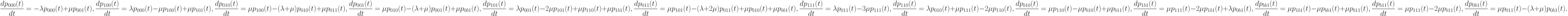 |
( 1.5) |
Система (1.5) — это система обыкновенных однородных дифференциальных уравнений с постоянными коэффициентами. Ее также можно представить в матричном виде:
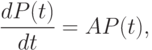
где:
 — вектор состояний системы 13-го порядка;
— вектор состояний системы 13-го порядка;
 — матрица постоянных коэффициентов размера
— матрица постоянных коэффициентов размера  .
.
Для решения системы (1.5) будем использовать естественные начальные условия, т. е.
 |
( 1.6) |
Отметим также, что система линейных дифференциальных уравнений будет иметь нетривиальное решение, если ее характеристический определитель будет равен нулю. В матричном виде получаем так называемое характеристическое уравнение
![det[sE-A]=0,](/sites/default/files/tex_cache/65ba15d18ca8b4c12b28ab46e8c97e11.png) |
( 1.7) |
где:
 — единичная матрица того же размера, что и матрица коэффициентов
— единичная матрица того же размера, что и матрица коэффициентов  ;
;
 — скалярная в общем случае комплексная переменная, относительно которой решается характеристическое уравнение.
— скалярная в общем случае комплексная переменная, относительно которой решается характеристическое уравнение.
Если действительная часть корней характеристического уравнения (1.7) будет отрицательной, то решение системы дифференциальных уравнений (1.5) с начальными условиями (1.6) будет устойчивым, т. е. будет стремиться к установившимся значениям.
Таким образом, система дифференциальных уравнений (1.5) с начальными условиями (1.6) представляет собой математическую модель трехфазной системы массового обслуживания с нулевой вместимостью блоков ожидания.
Схема трехфазной системы обслуживания показана на рис. 1.2.