Исследование качества генераторов случайных чисел

3. Исследование качества ГСЧ по критерию независимости случайных чисел с помощью нормированной автокорреляционной функции

Корреляционная функция называется автокорреляционной, если производится статистический анализ одного случайного процесса (или одной выборки случайных чисел).

Нормированной корреляционной функцией называется отношение центрированной корреляционной функции к дисперсии случайного процесса [4].

Для нахождения значений нормированной корреляционной функции необходимо предварительно центрировать значения случайного процесса или значения отсчетов случайной величины, т.е. выполнить операцию

,

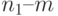где:

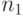— случайное число;

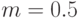— теоретическое математическое ожидание равномерного распределения.

Для определения корреляционной функции по результатам опыта выбирается достаточно большой объем выборки, чтобы можно было в широком диапазоне формировать разницу между двумя соседними значениями случайных чисел. Эту разницу для непрерывного времени обычно обозначают через и тогда корреляционная функция обозначается как 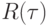. Если объем выборки составляет N, то диапазон вычисления корреляционной функции будет определяться как 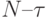. Величина задает область определения корреляционной функции. Например, может меняться от 0 до 6-8. При этом должно быть много больше 6 или 8. Область суммирования принимает значения от 1 (первое случайное число выборки) до .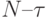

После этого корреляционная функция вычисляется по следующей экспериментальной формуле:

( 5.3)

где 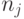— случайное число из заданной выборки случайных чисел.

Расчет по приведенной формуле: если взято какое-либо случайное число, то другое случайное число отстоит от первого на величину .

Обозначим нормированную корреляционную функцию как . Центрированную корреляционную функцию обозначим через . Тогда нормированная корреляционная функция будет определяться в виде отношения

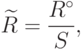
где — дисперсия данной выборки случайных чисел.

Вычисление можно выполнять по приведенной экспериментальной формуле (5.3), если в ней применяются центрированные случайные числа.

ГСЧ считается хорошим, если при , не равным нулю, модуль нормированной корреляционной функции меньше 0.1, т. е. .

Приведем пример программного анализа независимости последовательности случайных чисел, формируемых функцией , с помощью автокорреляционной функции.

Программный код решения примера:

clear,clc
%% Ввод параметров в интерактивном режиме
V1 = inputdlg({'Введите число больше 10.......................................',...
    'Сдвиг больше 1'},'Корреляционная функция',1,{'800','6'});

%% Преобразование к числам с плавающей точкой
V2 = str2num(char(V1));
% Гарантированное выделение целой части
V = fix(V2(1));
z = fix(V2(2));
% Формирование выборки случайных чисел
N = rand(V,1); 
%% Центрирование выборки случайных чисел относительно математического ожидания
Nc = N - 0.5;

%% Расчет автокорреляционной функции
sum1 = Nc(1:(V-z));
sum2 = Nc((1+z):V);
Rc = sum(sum1.*sum2)/(V-z);
s = var(N);
Rn = (Rc/s);
%% Проверка качества случайных чисел
if abs(Rn) < 0.1
   fprintf('\n\t ГСЧ выcокого качеcтва\n')
else
   fprintf('\n\t ГСЧ низкого качеcтва\n')
end
%% Интерактивное сообщение
helpdlg('Смотрите результаты в командном окне','Корреляционная функция')

В программе по умолчанию исследуется объем выборки величиной 800 со сдвигом между числами, равным 6.

Задание 6

1. Произведите расчет нормированной корреляционной функции для интервального сдвига в пределах от 0 до 50.
2. Постройте график нормированной автокорреляционной функции, т. е. зависимость от .
3. Произведите расчет нормированной корреляционной функции для объема выборки в соответствии с номером компьютера:

   Компьютер № 1: N = 410;     Компьютер № 2: N = 520;
   Компьютер № 3: N = 630;     Компьютер № 4: N = 740;
   Компьютер № 5: N = 850;     Компьютер № 6: N = 960;
   Компьютер № 7: N = 1070;   Компьютер № 8: N = 1180;
   Компьютер № 9: N = 1190;   Компьютер № 10: N = 1210.
4. Выполните первые три пункта задания для анализа ГСЧ в Excel.
5. Выполните первые три пункта задания для анализа ГСЧ в Delphi (консольное приложение).
6. Выполните первые три пункта задания для анализа ГСЧ в Pascal.
7. Выполните первые три пункта задания для анализа ГСЧ в С.
8. Выполните первые три пункта задания для анализа ГСЧ, созданного по методу срединных квадратов в MATLAB.
9. Выполните первые два пункта задания для анализа ГСЧ, созданного по методу Фибоначчи в MATLAB.
10. Выполните первые два пункта задания для анализа ГСЧ, созданного по линейному конгруэнтному методу в MATLAB.
11. Сделайте заключение о системе программирования, в которой ГСЧ является наиболее качественным.

Контрольные вопросы

1. По каким причинам не имеет практического применения метод срединных квадратов?
2. Как осуществляется статистическая оценка программных генераторов псевдослучайных чисел?
3. Что означает конгруэнтность двух чисел по заданному модулю?
4. В программных генераторах псевдослучайных чисел используются детерминированные методы или вероятностные?
5. Что определяет собой корреляционная функция?
6. Что означает "центрированная автокорреляционная функция"? Для чего она применяется?
7. Что определяет собой тест критерия Колмогорова–Смирнова?
8. Что определяет собой длина периода генератора псевдослучайных чисел?