НОУ ИНТУИТ | Моделирование систем. Лекция 9: Планирование и обработка результатов пассивного эксперимента

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

Мордовский государственный университет имени Н.П. Огарева

Опубликован: 30.11.2010 | Доступ: свободный | Студентов: 3283 / 1985 | Оценка: 4.12 / 4.13 | Длительность: 14:37:00

ISBN: 978-5-9963-0352-6

Темы: Программирование, Алгоритмы и дискретные структуры

Специальности: Программист, Системный архитектор

|

Вам нравится? Нравится 30 студентам

| Поделиться |

Поддержать курс

| Скачать электронную книгу

3. Оценка параметров многомерной функции ОТ-клика

Пример 4. Поставим задачу оценки параметров 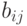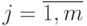$b_{0i}$ , $b_{ij}$ , $i=\overline{1,n}$ , $j=\overline{1,m}$ многомерной функции отклика вида

$y_1=b_{01}+b_{11}x_1+b_{12}x_2+...+b_{1j}x_j+...+b_{1m}x_m,\\ y_2=b_{02}+b_{21}x_1+b_{22}x_2+...+b_{2j}x_j+...+b_{2m}x_m,\\ .......................................\\ y_i=b_{0i}+b_{i1}x_1+b_{i2}x_2+...+b_{ij}x_j+...+b_{im}x_m,\\ .......................................\\ y_n=b_{0n}+b_{n1}x_1+b_{n2}x_2+...+b_{nj}x_j+...+b_{nm}x_m$

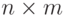по известным средним значениям независимых аргументов $x_{j}$ , число которых , и по известным средним значениям самих функций $y_{i}$ , число которых . Будем считать, что совокупность повторных значений функций распределена по нормальному закону, а аргументы функций могут быть распределены произвольно. Параметры многомерной функции отклика образуют матрицу размера $n\times m$ . Эту матрицу обозначим как .

Как видно, функции отклика являются линейными как по своим аргумента, так и по параметрам. В связи с этим для оценки параметров по измерениям аргументов и функций отклика (повторным значениям) целесообразно применить метод наименьших квадратов.

Программный код решения примера:

clear,clc
%---------------------------------------------------------------
options.Resize = 'on';
   options.WindowStyle = 'normal';
   options.Interpreter = 'tex';
   yx = inputdlg({'\bfСредние значения функций отклика:',...
        '\bfСредние значения аргументов функции отклика:',...
        '\bfЧисло измерений:',...
        '\bfВеличина стандартного отклонения функции откли-ка:.....'},...
'ИСХОДНЫЕ ДАННЫЕ',1,{'1,2,3,4,5,6,7,8','11,23,4,7,9','50','0.1'},options);

% БАЗОВЫЕ ВЕКТОРЫ ВЫХОДА, ВХОДА, ЧИСЛО ИЗМЕРЕНИЙ, 
% СТАНДАРТНОЕ ОТКЛОНЕНИЕ
Yb = str2num(char(yx(1)));
Ub = str2num(char(yx(2)));
r = str2num(char(yx(3)));
s = str2num(char(yx(4)));
%-------------------------------------------------------------------
% ПРОВЕРКА ВВОДА ДАННЫХ
if ( isempty(Yb) == 1 | isreal(Yb) == 0 | isinf(Yb) == 1 )
    errordlg(sprintf('Значения функций должны составлять вектор действительных чисел'),'Ошибка ввода значений функций')
   return

elseif ( min(size(Yb)) > 1 & max(size(Yb)) > 1 )
   errordlg(sprintf('Значения функций должны составлять вектор, не матрицу'),'Ошибка ввода значений функций')
   return
end
%----------------------------------------------------------------
%% ПРИВЕДЕНИЕ К ВЕКТОРУ-СТРОКЕ
[ry,vy] = size(Yb);
if ( ry == 1 )
    Yb = Yb;
elseif ( ry > 1 )
    Yb = Yb';
end
if ( isempty(Ub) | ~isreal(Ub) | isinf(Ub) )
    errordlg(sprintf('Значения аргументов должны составлять вектор действительных чисел'), ...
        'Ошибка ввода значений аргументов')
    return
elseif ( min(size(Ub)) > 1 & max(size(Ub)) > 1 )
   errordlg('Значения аргументов функций должны составлять вектор, не матрицу','Ошибка ввода значений аргументов функций')
   return
elseif ( isempty(find(Ub == 0)) == 0 )
    errordlg(sprintf('Значения аргументов функций не должны быть нулевыми'),'Ошибка ввода значений аргументов')
   return
end
%--------------------------------------------------------------
%% ПРИВЕДЕНИЕ К ВЕКТОРУ-СТРОКЕ
[ru,vu] = size(Ub);
if ( ru == 1 )
    Ub = Ub;
elseif ( ru > 1 )
    Ub = Ub';
end
if ( isempty(r) | ~isreal(r) | isinf(r) | r <= 0 )
    errordlg('Число измерений должно быть натуральным числом',...
               'Ошибка ввода числа измерений')
    return
elseif ( length(r) > 1 | r ~= round(r))
   errordlg('Число измерений должно быть одним натуральным числом',...
             'Ошибка ввода числа измерений')
   return

elseif ( r <= length(Yb)*(length(Ub) + 1) )
    errordlg(sprintf('Число измерений должно быть не меньше произведения числа функций на число аргументов плюс 1: больше %d',...
length(Yb)*(length(Ub) + 1)), 'Ошибка ввода числа измерений')
    return
end
%-----------------------------------------------------------------
if ( isempty(s) | ~isreal(s) | isinf(s) )
errordlg('Стандартное отклонение должно быть действительным числом',...
 'Ошибка ввода стандартного отклонения')
    return
elseif ( length(s) > 1 )
   errordlg('Стандартное отклонение должно быть одним действительным числом','Ошибка ввода стандартного отклонения')
   return
elseif ( s <= 0 )
    errordlg('Стандартное отклонение должно быть больше нуля',...
        'Ошибка ввода отклонения')
    return
end
%----------------------------------------------------------------
% % ЗАДАНИЕ r  ИЗМЕРЕНИЙ ФУНКЦИЙ ОТКЛИКА
Y = [];
 for k = 1 : length(Yb)
    for I = 1 : r
         Y(:,k) = Yb(k) + normrnd(0,s,r,1);
    end
end
% % ЗАДАНИЕ r  ИЗМЕРЕНИЙ АРГУМЕНТОВ ФУНКЦИИ ОТКЛИКА 
 X = [];
for m = 1 : length(Ub)
    for J = 1 : r
    X(:,m) = Ub(m) + rand(r,1);
end
end
%% ВВЕДЕНИЕ ФИКТИВНОГО АРГУМЕНТА, РАВНОГО ЕДИНИЦЕ
X1 = [ones(r,1),X];
%% РАСЧЕТ ПАРАМЕТРОВ ФУНКЦИИ ОТКЛИКА
 B = (inv(X1'*X1)*X1'*Y)';
 %% ВЫВОД РЕЗУЛЬТАТОВ
 fprintf('\n\t ИСХОДНЫЕ ДАННЫЕ ЭКСПЕРИМЕНТА:\n')
fprintf('\t Вектор-строка значений функции отклика:\n')
fprintf('\t %g',Yb)
fprintf('\n')
fprintf('\t Вектор-строка значений аргументов:\n')
fprintf('\t %g',Ub)
fprintf('\n')
fprintf('\t Заданное число повторных измерений: r = %d\n',r)
fprintf('\t Стандартное отклонение повторных измерений функций: s = %g\n',s)
disp('-----------------------------------------------------------')
fprintf('\t РЕЗУЛЬТАТЫ ПАССИВНОГО МНОГОМЕРНОГО ЭКСПЕРИМЕНТА\n')
fprintf('\t ОЦЕНКА МАТРИЦЫ ПАРАМЕТРОВ:\n')
 disp(B)
 %% РАСЧЕТНЫЕ ЗНАЧЕНИЯ ФУНКЦИЙ
 
Ybpac = B*[1,Ub]';
disp('------------------------------------------------------------')
fprintf('\t СРАВНЕНИЕ ЗНАЧЕНИЙ ЗАДАННЫХ ФУНКЦИЙ И РАСЧЕТНЫХ:\n')
disp([Yb' Ybpac])
disp('------------------------------------------------------------')
helpdlg(sprintf('Результаты выполнения программы смотрите в командном окне'),'')

Пример выполнения программы без демонстрации диалоговых окон

ИСХОДНЫЕ ДАННЫЕ ЭКСПЕРИМЕНТА
	 Вектор-строка значений функции отклика:
	 1	 2	 3	 4	 5	 6	 7	 8
	 Вектор-строка значений аргументов:
	 11	 23	 4	 7	 9
	 Заданное число повторных измерений: r = 50
	 Стандартное отклонение повторных измерений функций: s = 0.1
-----------------------------------------------------------
	 РЕЗУЛЬТАТЫ ПАССИВНОГО МНОГОМЕРНОГО ЭКСПЕРИМЕНТА
	 ОЦЕНКА МАТРИЦЫ ПАРАМЕТРОВ:
   -1.5280   -0.0296    0.0969   -0.0103   -0.0108    0.0767
    3.1418   -0.0457   -0.0015    0.0794   -0.0597   -0.0519
    2.2212   -0.0010    0.0370   -0.0022    0.0191   -0.0225
    4.3340   -0.1121    0.0989   -0.0480    0.0087   -0.1287
    1.3881    0.0194    0.0830   -0.0053    0.0519    0.1112
    8.1169   -0.0406   -0.1085    0.0382   -0.0001    0.0760
    9.9112   -0.0201   -0.0095    0.0651   -0.0843   -0.0143
    8.1976    0.0707   -0.0004   -0.0371   -0.0408   -0.0563
------------------------------------------------------------
	 СРАВНЕНИЕ ЗНАЧЕНИЙ ЗАДАННЫХ ФУНКЦИЙ И РАСЧЕТНЫХ:
    1.0000    0.9483
    2.0000    2.0366
    3.0000    2.9832
    4.0000    4.0865
    5.0000    4.8532
    6.0000    6.0105
    9.0000    9.0124
    8.0000    8.0252
------------------------------------------------------------

Примечание. Обратите внимание на зависимость полученных результатов относительно задаваемого стандартного отклонения, применяемого для формирования повторных измерений функций отклика.

Задание 4

Результат выполнения программы запишите в текстовый файл с именем compX.txt, где — номер компьютера, за которым выполняется лабораторная работа (1, 2, 3, ...).
Дополните программу вычислением отдельных составляющих заданной многомерной функции отклика.
Напишите фрагмент программы по расчету относительной и, возможно, абсолютной погрешности относительно заданных значений функций отклика.
Рассчитайте остаточную сумму квадратов по составляющим функции отклика.
Видоизмените программу для оценки параметров многомерной функции отклика для случая, когда в уравнениях отсутствуют свободные слагаемые $b_{0i}, i = 1, 2, …, n$ .

Контрольные вопросы

В чем заключается основная задача пассивного эксперимента?
Что такое линейный регрессионный анализ?
Что называется спектром плана в пассивном эксперименте?
Как рассчитывается аппроксимирующий полином?
Что называется факторным пространством?
Когда применяется матрица плана с первым столбцом, состоящим из единиц?
Когда существует единственное решение нормального уравнения?
Какова размерность информационной матрицы в нормальном регрессионном уравнении?

Дальше >>

Авторизоваться

Моделирование систем

Планирование и обработка результатов пассивного эксперимента

3. Оценка параметров многомерной функции ОТ-клика

Контрольные вопросы

Вопросы и ответы