|
Добрый день. Я приступила сегодня к самостоятельному изучению курса "Моделирование систем". Хочу понять - необходимо ли отсылать мои решения практических заданий на сайт, (и если да - то где найти волшебную кнопку "Загрузить...") или практические задания остаются полностью на моей совести? (никто не проверяет, и отчётности по ним я предоставлять не обязана?) P.S.: тьютора я не брала |
Моделирование многоканальных систем массового обслуживания
2.2. Пример моделирования системы типа М/М/M/K с ограниченным временем ожидания
Пример 2. Получите операционные характеристики системы  с ограниченным временем ожидания при следующих параметрах системы:
с ограниченным временем ожидания при следующих параметрах системы: 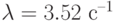 — интенсивность входного потока требований,
— интенсивность входного потока требований,  — интенсивность обслуживания каждым прибором,
— интенсивность обслуживания каждым прибором, 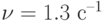 — интенсивность ухода из очереди "нетерпеливых" требований. Моделирование проведите в MATLAB и GPSS/PC.
— интенсивность ухода из очереди "нетерпеливых" требований. Моделирование проведите в MATLAB и GPSS/PC.
Размеченный граф состояний системы показан на рис. 2.3.
На рис. 2.3 вокруг состояния 4 проведена воображаемая окружность для пояснения применения мнемонического правила составления дифференциальных уравнений Колмогорова. В соответствии с мнемоническим правилом получаем следующую систему дифференциальных уравнений:
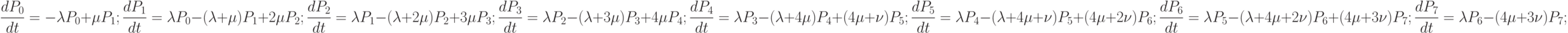
где  — вероятности состояний системы.
— вероятности состояний системы.
Для интегрирования системы дифференциальных уравнений зададим естественные граничные условия:

Программный код решения примера в системе MATLAB:
function MMmKv
%% Система M/M/4/7 с ограниченным временем ожидания в очереди
% Параметры системы
L = 3.52;
M = 0.678;
v = 1.3;
m = 4;
K = 7;
% Матрица коэффициентов системы дифференциальных уравнений
global A
A = [-L, M, zeros(1,6);
L, -(L+M), 2*M, zeros(1,5);
0, L, -(L+2*M), 3*M, zeros(1,4);
0, 0, L, -(L+3*M), 4*M, zeros(1,3);
zeros(1,3), L, -(L+4*M), (4*M+v), 0, 0;
zeros(1,4), L, -(L+4*M+v), (4*M+2*v), 0;
zeros(1,5), L, -(L+4*M+2*v), (4*M+3*v);
zeros(1,6), L ,-(4*M+3*v)];
% Решение дифференциальных уравнений
T = [0,20]; % Время интегрирования
P0 = [1;zeros(length(A)-1,1)]; % Начальные условия
[t, P] = ode23(@cmo, T, P0);
%% Построение диаграмм вероятностей состояний
% line(t,P,'linew',2) %% сполошные линии с различными цветами
line(t,P(:,1),'linew',2, 'color','r') %% Po
line(t,P(:,2), 'linew',2,'lines','--') %% P1
line(t,P(:,3), 'linew',2,'lines','-.') %% P2
line(t,P(:,4), 'linew',2,'lines',':') %% P3
line(t,P(:,5), 'marker','o', 'color', 'm') %% P4
line(t,P(:,6), 'marker','h', 'color','k') %% P5
line(t,P(:,7), 'marker','p','color','r') %% P6
line(t,P(:,8), 'marker','>') %% P7
grid on
N = length(A)-1;
arr = [0:N]';
str = num2str(arr);
legend(strcat('\bf\itP\rm\bf_', str, '(\itt\rm\bf)'));
title(sprintf('%s Вероятности состояний системы M/M/%d/%d', '\bf\fontsize{12}',m, K));
xlabel('\bf\it\fontsize{12} - - - - - - - - t - - - - - - - -')
ylabel('\bf\fontsize{12}\itP\rm\bf(\itt\rm\bf)');
set(gca, 'fontweight','bold', 'fontsize',10)
Pcm = P(end,:); % Стационарные вероятности
fprintf('\n Стационарные вероятности:\n');
for J = 1 : length(A)
fprintf('\tP%d = %f\n', J-1, Pcm(J));
end
fprintf('\n\t ОПЕРАЦИОННЫЕ ХАРАКТЕРИСТИКИ:\n');
Pnot = P(end,end);
fprintf(' Вероятность отказа Pnot = %f\n', P(end,end));
Q = 1 - Pnot;
fprintf(' Относительная пропускная способность Q = %f\n', Q);
Ab = L*Q;
fprintf(' Абсолютная пропускная способность A = %f\n', Ab);
Pq = sum(P(end, m+1:end));
fprintf(' Вероятность наличия очереди Pq = %f\n', Pq);
Ps = sum(P(end, m:end));
fprintf(' Вероятность загрузки всех каналов обслуживания Ps = %f\n', Ps);
Ns = [0:length(A)-1]*P(end,:)';
fprintf(' Среднее количество требований в системе Ns = %f\n', Ns);
fprintf(' Среднее время пребывания требования в системе Ts = %f\n', Ns/L);
Nq = [0:(K-m)]*P(end,m:K)';
fprintf(' Средняя длина очереди Nq = %f\n', Nq);
fprintf(' Среднее время пребывания требования в очереди Tq = %f\n', Nq/L);
function f = cmo(t,P);
%% Функция описания правых частей
%% дифференциальных уравнений
global A
f = A*P;Результат выполнения программы
Стационарные вероятности: P0 = 0.007887 P1 = 0.040947 P2 = 0.106289 P3 = 0.183963 P4 = 0.238701 P5 = 0.209568 P6 = 0.138707 P7 = 0.073939 ОПЕРАЦИОННЫЕ ХАРАКТЕРИСТИКИ Вероятность отказа: Pnot = 0.073939 Относительная пропускная способность: Q = 0.926061 Абсолютная пропускная способность: A = 3.259736 Вероятность наличия очереди: Pq = 0.660915 Вероятность загрузки всех каналов обслуживания: Ps = 0.844877 Среднее количество требований в системе: Ns = 4.157868 Среднее время пребывания требования в системе: Ts = 1.181213 Средняя длина очереди: Nq = 1.073958 Среднее время пребывания требования в очереди: Tq = 0.305102
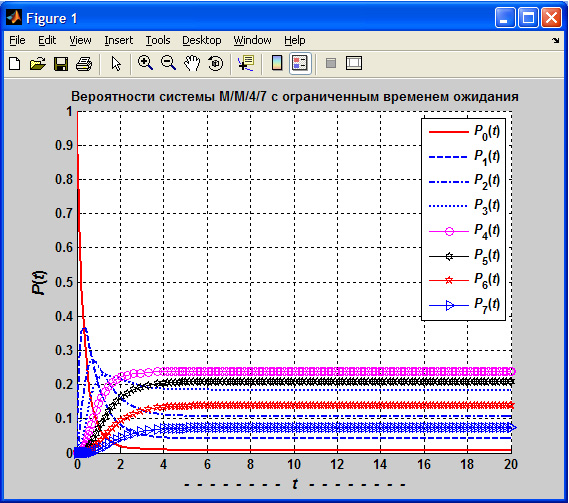
Диаграмма вероятностей состояний системы  с ограниченным временем ожидания показана на рис. 2.4.
с ограниченным временем ожидания показана на рис. 2.4.
Задание 3
- Постройте зависимость среднего времени пребывания в очереди от интенсивности входного потока, изменяя интенсивность от
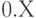 до
до 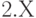 , где
, где  — номер компьютера (1, 2, 3, ...), за которым выполняется лабораторная работа.
— номер компьютера (1, 2, 3, ...), за которым выполняется лабораторная работа. - Напишите программу для анализа системы с параметрами, вводимыми с клавиатуры пользователем, т. е.
 ,
,  ,
,  ,
,  ,
,  . Предусмотрите также ввод интервала интегрирования дифференциальных уравнений.
. Предусмотрите также ввод интервала интегрирования дифференциальных уравнений.
Для решения примера в системе GPSS/PC подготовим данные о функциях распределения входного потока, экспоненциальном обслуживании и экспоненциальном уходе из очереди "нетерпеливых" требований.
Программа в MATLAB формирования данных:
clear all,clc
L = 3.52; %% Интенсивность входного потока
M = 0.678; %% Интенсивность обслуживания
v = 1.3; %% Интенсивность ухода из очереди
%% Функции экспоненциального распределения
x = 0 : 0.2 : 20;
F = 1 - exp(-L*x);
F2 = 1 - exp(-M*x);
F3 = 1 - exp(-v*x);
%%% Запись в текстовый файл MC2.txt
fid = fopen('MC2.txt', 'w');
%% Для блока generate
fprintf(fid, 'puas function RN1,C50\r\n');
for J = 1 : length(x)
if J <= 50
if mod(J, 5)
fprintf(fid, '%g,%g/', F(J), x(J));
else
fprintf(fid, '\r\n');
fprintf(fid, '%g,%g/', F(J), x(J));
end
end
end
fprintf(fid, '\r\n;-----------------------------------\r\n');
%% Для блоков advance
fprintf(fid, '\r\nexpM function RN2,C50\r\n');
for J = 1 : length(x)
if J <= 50
if mod(J, 5)
fprintf(fid, '%g,%g/', F2(J), x(J));
else
fprintf(fid, '\r\n');
fprintf(fid, '%g,%g/', F2(J), x(J));
end
end
end
fprintf(fid, '\r\n;-----------------------------------\r\n');
%% Для функции распределения ухода из очереди
fprintf(fid, '\r\nexpM function RN3,C50\r\n');
for J = 1 : length(x)
if J <= 50
if mod(J, 5)
fprintf(fid, '%g,%g/', F3(J), x(J));
else
fprintf(fid, '\r\n');
fprintf(fid, '%g,%g/', F3(J), x(J));
end
end
end
fclose(fid);GPSS-программа приводится ниже. В ней задано условие обработки 1000 требований.
Программный код решения примера в системе GPSS/PC:
simulate puas function RN1,C50 0,0/0.505397,0.2/0.755368,0.4/0.879004,0.6/ 0.940155,0.8/0.970401,1/0.98536,1.2/0.992759,1.4/0.996419,1.6/ 0.998229,1.8/0.999124,2/0.999567,2.2/0.999786,2.4/0.999894,2.6/ 0.999948,2.8/0.999974,3/0.999987,3.2/0.999994,3.4/0.999997,3.6/ 0.999998,3.8/0.999999,4/1,4.2/1,4.4/1,4.6/ 1,4.8/1,5/1,5.2/1,5.4/1,5.6/ 1,5.8/1,6/1,6.2/1,6.4/1,6.6/ 1,6.8/1,7/1,7.2/1,7.4/1,7.6/ 1,7.8/1,8/1,8.2/1,8.4/1,8.6/ 1,8.8/1,9/1,9.2/1,9.4/1,9.6/ 1,9.8/ ;----------------------------------- expM function RN2,C50 0,0/0.126808,0.2/0.237536,0.4/0.334223,0.6/ 0.418649,0.8/0.492369,1/0.556741,1.2/0.612949,1.4/0.662031,1.6/ 0.704888,1.8/0.742311,2/0.774988,2.2/0.803521,2.4/0.828436,2.6/ 0.850192,2.8/0.869189,3/0.885777,3.2/0.900261,3.4/0.912909,3.6/ 0.923953,3.8/0.933596,4/0.942017,4.2/0.949369,4.4/0.95579,4.6/ 0.961396,4.8/0.966291,5/0.970566,5.2/0.974298,5.4/0.977558,5.6/ 0.980403,5.8/0.982888,6/0.985058,6.2/0.986953,6.4/0.988607,6.6/ 0.990052,6.8/0.991314,7/0.992415,7.2/0.993377,7.4/0.994217,7.6/ 0.99495,7.8/0.995591,8/0.99615,8.2/0.996638,8.4/0.997064,8.6/ 0.997437,8.8/0.997762,9/0.998045,9.2/0.998293,9.4/0.99851,9.6/ 0.998699,9.8/ ;----------------------------------- expV function RN3,C50 0,0/0.228948,0.2/0.405479,0.4/0.541594,0.6/ 0.646545,0.8/0.727468,1/0.789864,1.2/0.837974,1.4/0.87507,1.6/ 0.903672,1.8/0.925726,2/0.942731,2.2/0.955843,2.4/0.965953,2.6/ 0.973748,2.8/0.979758,3/0.984392,3.2/0.987966,3.4/0.990721,3.6/ 0.992845,3.8/0.994483,4/0.995746,4.2/0.99672,4.4/0.997471,4.6/ 0.99805,4.8/0.998497,5/0.998841,5.2/0.999106,5.4/0.999311,5.6/ 0.999469,5.8/0.99959,6/0.999684,6.2/0.999756,6.4/0.999812,6.6/ 0.999855,6.8/0.999888,7/0.999914,7.2/0.999934,7.4/0.999949,7.6/ 0.999961,7.8/0.99997,8/0.999977,8.2/0.999982,8.4/0.999986,8.6/ 0.999989,8.8/0.999992,9/0.999994,9.2/0.999995,9.4/0.999996,9.6/ 0.999997,9.8/ *************************************** T_s table m1,0,2,6 ************************************** 10 GENERATE fn$puas 20 test LE q1,3,exit1 30 test L qx1,fn$expV,exit2 40 QUEUE 1 50 TRANSFER ALL,CHAN1,CHAN4,3 ************************************** 100 CHAN1 SEIZE zet1 110 assign 1,zet1 120 transfer ,come ************************************** 200 chan2 SEIZE zet2 210 assign 1,zet2 220 transfer ,come ************************************** 300 chan3 SEIZE zet3 310 assign 1,zet3 320 transfer ,come ************************************** 400 chan4 SEIZE zet4 410 assign 1,zet4 ************************************** 510 come DEPART 1 520 advance fn$expM 530 release p1 540 tabulate T_s 550 work terminate 1 560 exit1 terminate 570 exit2 terminate ************************************** START 1000 ;end
В программе использованы следующие стандартные числовые атрибуты:  — длина первой очереди,
— длина первой очереди, 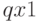 — среднее время пребывания в первой очереди без нулевых входов,
— среднее время пребывания в первой очереди без нулевых входов,  — время пребывания транзакта в модели. Освобождение того или иного устройства блоком
— время пребывания транзакта в модели. Освобождение того или иного устройства блоком  выполнено на основе записи в первый параметр транзактов имени устройства, например,
выполнено на основе записи в первый параметр транзактов имени устройства, например,  .
.
Программа реализует следующий алгоритм. Поступающие по пуассоновскому закону требования (транзакты в системах GPSS) попадают в очередь на обслуживание. Если в очереди меньше или равно 3 транзактам, то они ожидают начала обслуживания. В противном случае они покидают систему по метке  . Проверка длины очереди осуществляется блоком
. Проверка длины очереди осуществляется блоком  в строке 20. Время ожидания соотносится со случайным временем ожидания "нетерпеливых" требований —— со значением функции распределения
в строке 20. Время ожидания соотносится со случайным временем ожидания "нетерпеливых" требований —— со значением функции распределения  . Если оно меньше, то требования поступают в устройства обслуживания, в одно из свободных устройств, начиная с первого (реализуется блоком
. Если оно меньше, то требования поступают в устройства обслуживания, в одно из свободных устройств, начиная с первого (реализуется блоком 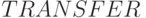 в режиме
в режиме 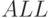 ). Поступающим в устройства обслуживания транзактам в первый параметр записывается имя устройства (
). Поступающим в устройства обслуживания транзактам в первый параметр записывается имя устройства (  ), после чего они отправляются по метке
), после чего они отправляются по метке 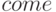 в блок
в блок  , который освобождает одно место в очереди под номером 1. Далее происходит обслуживание транзактов по экспоненциальному закону блоком
, который освобождает одно место в очереди под номером 1. Далее происходит обслуживание транзактов по экспоненциальному закону блоком  в строке 520. Вывод транзакта из работающего устройства осуществляется блоком
в строке 520. Вывод транзакта из работающего устройства осуществляется блоком  по первому параметру, в котором записано имя устройства. Обслуженные транзакты выводятся из системы блоком
по первому параметру, в котором записано имя устройства. Обслуженные транзакты выводятся из системы блоком 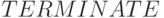 с меткой
с меткой  .
.
Для получения распределения времени пребывания в модели использован оператор таблицы  с меткой
с меткой  . Сбор статистики для введенной таблицы осуществляется блоком
. Сбор статистики для введенной таблицы осуществляется блоком 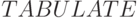 .
.
Результат выполнения программы система GPSS/PC оформляет в виде файла стандартного отчета, который имеет следующий вид:
GPSS/PC Report file REPORT.GPS. (V 2, # 37349) 01-08-2010 11:16:14 page 1
START_TIME END_TIME BLOCKS FACILITIES STORAGES FREE_MEMORY
0 416 23 4 0 137072
LINE LOC BLOCK_TYPE ENTRY_COUNT CURRENT_COUNT RETRY
10 1 GENERATE 14227 0 0
20 2 TEST 14227 0 0
30 3 TEST 13127 0 0
40 4 QUEUE 1002 0 0
50 5 TRANSFER 1288 1 0
100 CHAN1 SEIZE 317 0 0
110 7 ASSIGN 317 0 0
120 8 TRANSFER 317 0 0
200 CHAN2 SEIZE 265 0 0
210 10 ASSIGN 265 0 0
220 11 TRANSFER 265 0 0
300 CHAN3 SEIZE 232 0 0
310 13 ASSIGN 232 0 0
320 14 TRANSFER 232 0 0
400 CHAN4 SEIZE 187 0 0
410 16 ASSIGN 187 0 0
510 COME DEPART 1001 0 0
520 18 ADVANCE 1001 1 0
530 19 RELEASE 1000 0 0
540 20 TABULATE 1000 0 0
550 WORK TERMINATE 1000 0 0
560 EXIT1 TERMINATE 1100 0 0
570 EXIT2 TERMINATE 12125 0 0
FACILITY ENTRIES UTIL. AVE._TIME AVAILABLE OWNER PEND INTER RETRY DELAY
ZET1 317 0.776 1.02 1 0 0 0 1 0
ZET2 265 0.675 1.06 1 14161 0 0 1 0
ZET3 232 0.557 1.00 1 0 0 0 1 0
ZET4 187 0.507 1.13 1 0 0 0 1 0
QUEUE MAX CONT. ENTRIES ENTRIES(0) AVE.CONT. AVE.TIME AVE.(-0) RETRY
1 4 1 1002 765 0.72 0.30 1.27 0
TABLE MEAN STD.DEV. RETRY RANGE FREQUENCY CUM.%
T_S 1.34 1.58 0
- 0 374 37.40
0 - 2 448 82.20
2 - 4 122 94.40
4 - 6 42 98.60
6 - 8 14 100.00
XACT_GROUP GROUP_SIZE RETRY
POSITION 0 0По файлу стандартного отчета определим следующие операционные характеристики: среднее время пребывания в очереди и среднее время пребывания в модели (в системе). Эти характеристики обозначим  и
и  соответственно.
соответственно.
Значение  расположено в поле
расположено в поле  статистики очереди. Оно равно
статистики очереди. Оно равно  .
.
Значение Ts есть среднее значение таблицы 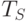 , т. е. в поле
, т. е. в поле 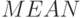 . Оно равно
. Оно равно  .
.
Поскольку очередь имеет нулевые входы – поле  , для расчета средней длины очереди
, для расчета средней длины очереди  используем аналог формулы Литтла [2], т. е.
используем аналог формулы Литтла [2], т. е.

Для определения среднего количества требований 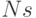 в системе используем формулу Литтла:
в системе используем формулу Литтла:

Задание 4
- По данным файла стандартного отчета определите вероятность отказа, относительную пропускную способность, абсолютную пропускную способность.
- Если требуется, то внесите изменения в программу для определения ве-роятности наличия очереди и вероятности загрузки всех каналов обслуживания.
- Внесите изменения в программу для определения вероятностей состояния системы.
- Полученные результаты сведите в таблицу, в которую также внесите операционные характеристики системы
 с ограниченным временем ожидания, полученные с помощью анализа в MATLAB.
с ограниченным временем ожидания, полученные с помощью анализа в MATLAB.