|
Добрый день. Я приступила сегодня к самостоятельному изучению курса "Моделирование систем". Хочу понять - необходимо ли отсылать мои решения практических заданий на сайт, (и если да - то где найти волшебную кнопку "Загрузить...") или практические задания остаются полностью на моей совести? (никто не проверяет, и отчётности по ним я предоставлять не обязана?) P.S.: тьютора я не брала |
Моделирование многоканальных систем массового обслуживания
Теоретическая часть
Многоканальные системы массового обслуживания — это системы с параллельно включенными приборами обслуживания. Для них принято использовать символику Кендалла, которая состоит из основных четырех позиций вида 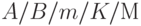 , где
, где  — закон поступления требований в систему,
— закон поступления требований в систему,  — закон обслуживания требований, m — число параллельно функционирующих приборов (каналов, узлов) обслуживания,
— закон обслуживания требований, m — число параллельно функционирующих приборов (каналов, узлов) обслуживания,  — допустимое число требований в системе, т. е. число требований в очереди плюс число требований, принятых на обслуживание. В системе
— допустимое число требований в системе, т. е. число требований в очереди плюс число требований, принятых на обслуживание. В системе 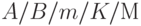 последний символ
последний символ  — число источников нагрузки [2]. При этом параметры системы постоянны, а процессы в системах рассматриваются с позиций теории размножения и гибели.
— число источников нагрузки [2]. При этом параметры системы постоянны, а процессы в системах рассматриваются с позиций теории размножения и гибели.
Предметом данной лабораторной работы будут системы с простейшим пуассоновским потоком, экспоненциальным обслуживанием и, возможно, экспоненциальном уходом из очереди "нетерпеливых" требований. При сделанных условиях исследуемые системы будут иметь следующие обозначения:  ,
, 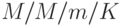 с нетерпеливыми требованиями,
с нетерпеливыми требованиями, 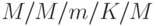 , где первые буквы
, где первые буквы  означают пуассоновский поток требований и экспоненциальное обслуживание, а в последнем примере крайняя правая буква
означают пуассоновский поток требований и экспоненциальное обслуживание, а в последнем примере крайняя правая буква  — это число требований, формируемых конечным числом источников нагрузки. В частности, может быть система с отказами, т. е.
— это число требований, формируемых конечным числом источников нагрузки. В частности, может быть система с отказами, т. е.  с отказами.
с отказами.
При моделировании сначала требуется составить дифференциальные уравнения относительно вероятностей состояний. Эти уравнения называются дифференциальными уравнениями Колмогорова [2]. При правильном составлении уравнений их решения при заданных начальных условиях стремятся к своим установившимся значениям. Эти значения называются стационарными вероятностями, на основе которых рассчитываются операционные характеристики системы.
Для составления уравнений Колмогорова можно использовать мнемоническое правило [4]. Сначала определим понятие потока вероятности: это такой поток, который переводит систему из одного состояния в другое соседнее и определяется как произведение вероятности 
 -го состояния, из которого происходит переход, на интенсивность потока событий (интенсивность поступления требований или интенсивность обслуживания). Теперь приведем мнемоническое правило составления уравнений Колмогорова: производная вероятности любого состояния равна сумме потоков вероятности, переводящих систему в это состояние, минус сумма всех потоков вероятности, выводящих систему из этого состояния [4].
-го состояния, из которого происходит переход, на интенсивность потока событий (интенсивность поступления требований или интенсивность обслуживания). Теперь приведем мнемоническое правило составления уравнений Колмогорова: производная вероятности любого состояния равна сумме потоков вероятности, переводящих систему в это состояние, минус сумма всех потоков вероятности, выводящих систему из этого состояния [4].
Прежде чем применять правило Колмогорова, целесообразно изобразить размеченный граф состояний заданной системы. На рис. 2.1 показан пример размеченного графа состояний для системы M/M/3/5 (  ,
,  ,
,  — интенсивность входного потока требований,
— интенсивность входного потока требований,  — интенсивность обслуживания одним прибором).
— интенсивность обслуживания одним прибором).
Используем мнемоническое правило составления уравнений Колмогорова для состояния 2, которое обведено окружностью. При этом потоки вероятности будут направлены по стрелкам. Если стрелка входит в окружность, то поток вероятности принимается положительным. Если стрелка выходит из окружности, то поток вероятности будет отрицательным. Относительно каждого состояния можно проводить воображаемую окружность. Дифференциальные уравнения имеют следующий вид:
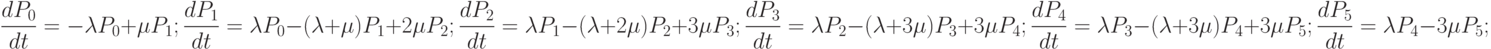 |
( 2.1) |
Для решения систем дифференциальных уравнений типа (2.1) обычно задают естественные начальные условия:
 |
( 2.2) |
Если в системе (2.1) производные приравнять нулю, то можно будет получить соотношения для расчета стационарных вероятностей состояний системы. При этом следует использовать нормировочное условие для 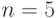 :
:
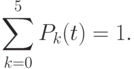 |
( 2.3) |
Практическая часть
2.1. Пример моделирования системы типа М/М/M/K
Система 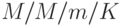 — это система с пуассоновским входящим потоком требований, с экспоненциальным законом обслуживания в m приборах, с допустимым числом требований в системе, не превышающим
— это система с пуассоновским входящим потоком требований, с экспоненциальным законом обслуживания в m приборах, с допустимым числом требований в системе, не превышающим  , которое не менее, чем заданное количество приборов обслуживания. Параметры системы постоянны, т. е.
, которое не менее, чем заданное количество приборов обслуживания. Параметры системы постоянны, т. е. 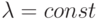 ,
, 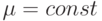 . Систему
. Систему 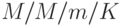 называют многоканальной системой массового обслуживания с ограниченной длиной очереди.
называют многоканальной системой массового обслуживания с ограниченной длиной очереди.
Пример 1. Проинтегрируйте систему массового обслуживания  при естественных граничных условиях и параметрах
при естественных граничных условиях и параметрах 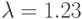 ,
,  . Рассчитайте операционные характеристики системы [2].
. Рассчитайте операционные характеристики системы [2].
Для решения примера сначала составим дифференциальные уравнения в соответствии с мнемоническим правилом Колмогорова:
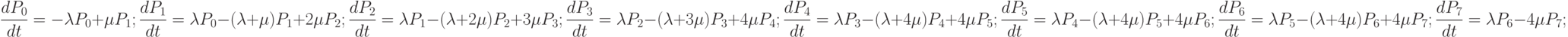
Естественные начальные условия:

Программный код решения примера в MATLAB:
function MMmK;
clc,close
% Параметры системы
L = 3.52;
M = 0.678;
m = 4;
K = 7;
%%%%%%%%%%%%%%%%%%%%%%%%
global A
A = [-L,M,0,0,0,0,0,0;
L,-(L+M),2*M,0,0,0,0,0;
0,L,-(L+2*M),3*M,0,0,0,0;
0,0,L,-(L+3*M),4*M,0,0,0;
0,0,0,L,-(L+4*M),4*M,0,0;
0,0,0,0,L,-(L+4*M),4*M,0;
0,0,0,0,0,L,-(L+4*M),4*M;
0,0,0,0,0,0,L,-4*M];
%% Численное интегрирование дифф. уравнений
P0 = [1;zeros(length(A)-1,1)];
T = [0,20];
[t,P] = ode23(@cmo, T, P0);
%% Построение диаграммы вероятностей состояний
%% line(t,P,'linew',2) %% с различными цветами
line(t,P(:,1),'linew',2, 'color','r') %% Po
line(t,P(:,2), 'linew',2,'lines','--') %% P1
line(t,P(:,3), 'linew',2,'lines','-.') %% P2
line(t,P(:,4), 'linew',2,'lines',':') %% P3
line(t,P(:,5), 'marker','o', 'color', 'm') %% P4
line(t,P(:,6), 'marker','h', 'color','k') %% P5
line(t,P(:,7), 'marker','p','color','r') %% P6
line(t,P(:,8), 'marker','>') %% P7
grid on
N = length(A)-1;
arr = [0:N]';
str = num2str(arr);
legend(strcat('\bf\itP\rm\bf_', str, '(\itt\rm\bf)'));
title(sprintf('%s Вероятности состояний системы M/M/%d/%d', '\bf\fontsize{12}',m, K));
xlabel('\bf\it\fontsize{12} - - - - - - - - t - - - - - - - -')
ylabel('\bf\fontsize{12}\itP\rm\bf(\itt\rm\bf)');
set(gca, 'fontweight','bold', 'fontsize',10)
fprintf('\n Стационарные вероятности:\n');
for J = 1 : length(A)
fprintf('\tP%d = %f\n', J-1, P(end,J));
end
fprintf('\n\t ОПЕРАЦИОННЫЕ ХАРАКТЕРИСТИКИ:\n');
Pnot = P(end,end);
fprintf(' Вероятность отказа Pnot = %f\n', P(end,end));
Q = 1 - Pnot;
fprintf(' Относительная пропускная способность Q = %f\n', Q);
Ab = L*Q;
fprintf(' Абсолютная пропускная способность A = %f\n', Ab);
Pq = sum(P(end, m+1:end));
fprintf(' Вероятность наличия очереди Pq = %f\n', Pq);
Ps = sum(P(end, m:end));
fprintf(' Вероятность загрузки всех каналов обслуживания Ps = %f\n', Ps);
Ns = [0:length(A)-1]*P(end,:)';
fprintf(' Среднее количество требований в системе Ns = %f\n', Ns);
fprintf(' Среднее время пребывания требования в системе Ts = %f\n', Ns/L);
Nq = [0:(K-m)]*P(end,m:K)';
fprintf(' Средняя длина очереди Nq = %f\n', Nq);
fprintf(' Среднее время пребывания требования в очереди Tq = %f\n', Nq/L);
function f = cmo(t,P);
%% Функция описания правых частей
%% дифференциальных уравнений
global A
f = A*P;Результат выполнения программы
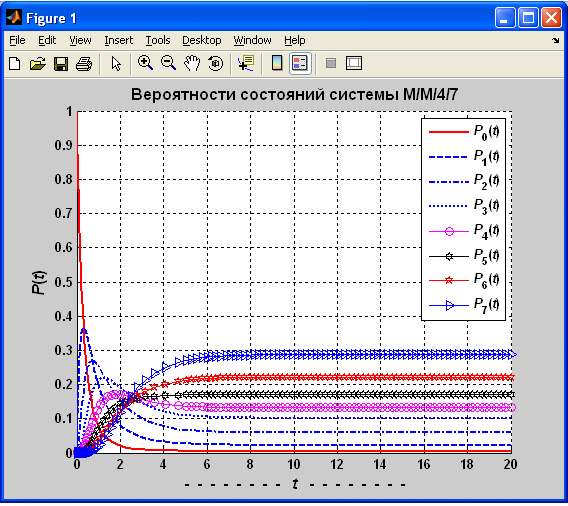
Стационарные вероятности: P0 = 0.004352 P1 = 0.022604 P2 = 0.058629 P3 = 0.101614 P4 = 0.131597 P5 = 0.171220 P6 = 0.221807 P7 = 0.288176 ОПЕРАЦИОННЫЕ ХАРАКТЕРИСТИКИ Вероятность отказа: Pnot = 0.288176 Относительная пропускная способность: Q = 0.711824 Абсолютная пропускная способность: A = 2.505620 Вероятность наличия очереди: Pq = 0.812800 Вероятность загрузки всех каналов обслуживания: Ps = 0.914415 Среднее количество требований в системе: Ns = 5.175269 Среднее время пребывания требования в системе: Ts = 1.470247 Средняя длина очереди: Nq = 1.139458 Среднее время пребывания требования в очереди: Tq = 0.323710
Среднее время пребывания требования в системе было рассчитано по формуле Литтла. Для расчета среднего времени пребывания требования в очереди использовался аналог формулы Литтла [2].
Диаграмма с вероятностями состояний системы  показана на рис. 2.2.
показана на рис. 2.2.
Задание 1
- Рассчитайте нормировочное условие для трех значений времени.
- Определите вероятность того, что в системе будет не более
 требований. Значение
требований. Значение  выбирайте случайно по равномерному закону из интервала целых чисел
выбирайте случайно по равномерному закону из интервала целых чисел ![[1; 6]](/sites/default/files/tex_cache/9d19931fb5629a2d703a6a8553085aca.png) (см.
(см.  ).
). - Примените диалоговое окно
 (см.
(см.  ) для ввода параметров системы.
) для ввода параметров системы. - Напишите программу для произвольно задаваемых параметров системы
 ,
,  и значений
и значений  ,
,  . Предусмотрите также ввод длительности интервала интегрирования.
. Предусмотрите также ввод длительности интервала интегрирования.