Физические основы работы акустических сенсоров. Приемники акустических сигналов. Некоторые интеллектуальные акустические сенсоры
Цель лекции: напомнить слушателям необходимые для понимания раздела сведения из физической акустики, в частности, основные формулы для расчета доплеровского сдвига частоты акустических волн при движении их излучателя и приемника. Объяснить принципы функционирования микрофонов, гидрофонов, стетоскопов, поверхностных микрофонов, роль микросистемных технологий в их усовершенствовании, указать области их применения. Привести показательные примеры интеллектуальных акустических сенсоров, показать их роль в современной жизни.
5.1. Физические основы работы акустических сенсоров
В акустических сенсорах первичные информационные сигналы являются акустическими. Это, например, звуки живой речи, музыка, пение птиц, сигналы эхолокации дельфинов или акустические сигналы в ультразвуковой диагностике, поверхностные акустические волны и т.п.
Напомним, что акустические волны – это колебания давления, распространяющиеся в воздухе (газах), жидкости или в твердой среде. Известно, что акустические волны распространяются значительно медленнее, чем радиоволны: в воздухе, например, со скоростью около 340 м/с, в воде – около 1,5 км/с, в твердых телах – 3-6 км/с. И это имеет свои положительные стороны.
По частоте колебаний акустические волны подразделяют на:
- инфразвуки (частота меньше 16 Гц);
- звуки (диапазон частот от 16 Гц до 20 кГц), которые воспринимает человеческое ухо;
- ультразвуки (от 20 кГц до 1 ГГц);
- гиперзвуки (свыше 1 ГГц, вплоть до 1013 Гц).
Инфразвуки в воде (напр., в морях и океанах) могут распространяться на сотни километров. Воспринимая их, обитатели моря заранее "слышат" приближение шторма. Гиперзвуки и ультразвуки сильно рассеиваются, поглощаются и поэтому затухают гораздо быстрее.
Ультразвуковые волны по частоте обычно делят на три диапазона:
- низкочастотный (16–100 кГц, длина волны в воздухе 3-20 мм, в воде 15-90 мм);
- средних частот (0,1-10 МГц, длина волны в воздухе 0,034–3,4 мм, в воде 0,15-15 мм);
- высокочастотный (10–1000 МГц, длина волны в воздухе 0,34-34 мкм, в воде 1,5–150 мкм).
Акустические волны естественного происхождения, как правило, являются сложными, несут с собой колебания разных частот. Их частотный состав обычно характеризуют частотно-амплитудным спектром – зависимостью интенсивности или амплитуды колебаний от частоты. Музыкальные звуки имеют в основном дискретный спектр, другие – непрерывный спектр. Звуковые шумы имеют очень широкий непрерывный спектр частот.
Интенсивность акустических, как и всех других видов волн характеризуют средней энергией, переносимой ими за единицу времени через единицу площади, перпендикулярной к направлению распространения, и измеряют в Вт/м2. Специфической характеристикой интенсивности акустических волн является амплитуда колебаний давления (Па). В области звуков, которые слышит человек, используют и логарифмическую меру громкости звука – так называемый " уровень звукового давления ". Его выражают в децибелах (дБ) и вычисляют по формуле
 |
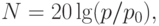( 5.1) |
– амплитуда колебаний давления в паскалях, а 
– это так называемый "порог слышимости", т.е. минимальная амплитуда звуковых колебаний, которые способно услышать человеческое ухо.При свободном распространении в однородной среде без поглощения и рассеяния интенсивность акустических волн уменьшается пропорционально квадрату расстояния от источника. В реальных средах имеют место поглощение, а также рассеяние акустических волн на неоднородностях, из-за чего интенсивность их с расстоянием убывает быстрее.
В акустических сенсорах часто используют эффект Доплера – изменение частоты колебаний, которые воспринимает наблюдатель, при движении источника волн или наблюдателя относительно друг друга или относительно той среды, в которой распространяются волны. Если наблюдатель неподвижен относительно среды распространения, а источник акустических волн приближается к наблюдателю со скоростью 
, то частота колебаний, которые воспринимает наблюдатель, определяется формулой
 |
( 5.2) |
– частота колебаний в источнике акустических волн,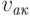 
– скорость распространения акустических волн в среде. Воспринимаемая нами частота акустических волн от источника, который к нам приближается, выше, а от источника, который от нас удаляется – ниже. По величине частотного сдвига можно определить скорость движения источника акустических волн относительно наблюдателя.Если, наоборот, источник акустических волн неподвижен относительно среды распространения, а наблюдатель приближается к источнику со скоростью , то частота колебаний, воспринимаемых наблюдателем, определяется по формуле
 |
( 5.3) |
Воспринимаемая нами частота выше, когда мы приближаемся к источнику, и ниже, когда мы отдаляемся от него.
Если источник акустических волн движется относительно среды со скоростью 
, а приемник – со скоростью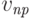 
навстречу источнику, то частота колебаний, которую он воспринимает, определяется по формуле
 |
( 5.4) |
В эхолокации важную роль играет и так называемый " двойной эффект Допплера " – изменение частоты колебаний звука при отражении акустических волн от подвижных объектов. Подвижный объект сначала выступает в роли приемника, а потом (при переизлучении) – в роли источника вторичных акустических волн. В этом случае изменение частоты вычисляется по формуле
 |
( 5.5) |
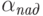и 
– углы между волновым вектором падающей либо отраженной волны и перпендикулярной составляющей скорости движения поверхности объекта соответственно. Если объект приближается к приемнику, то частота выше, а если отдаляется – ниже. По изменению частоты можно определить скорость движения объекта.Более детальную информацию относительно физики акустических волн можно получить из профессиональных книг, например [ [ 332 ] ].