|
Возможна ли разработка приложения на Octave с GUI? |
Обработка результатов эксперимента. Интерполяция функций
Пример 12.2. В результате опыта холостого хода определена зависимость потребляемой из сети мощности (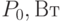 ) от входного напряжения (
) от входного напряжения (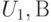 ) для асинхронного двигателя МТН111-6 (см. табл. 12.3). Построить график интерполяционной зависимости. Вычислить ожидаемое значение мощности при
) для асинхронного двигателя МТН111-6 (см. табл. 12.3). Построить график интерполяционной зависимости. Вычислить ожидаемое значение мощности при 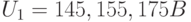 .
.
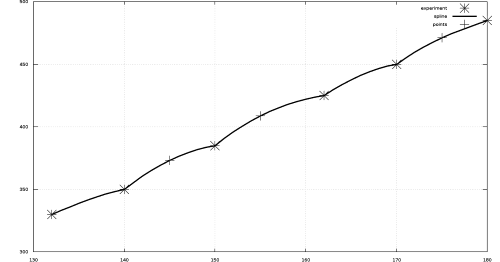
Реализуем рассмотренный ранее алгоритм кубического сплайна. Решение с комментариями представлено в листинге 12.5, а на рис. 12.2 можно увидеть графическое решение примера.
function[b, c, d]= koef_spline(x,y) % Функция вычисляет коэффициенты сплайна, здесь x,y — массивы абсцисс % и ординат экспериментальных точек, b, c, d — коэффициенты сплайна, % рассчитываемые по формулам (12.21), (12.23), (12.27), (12.30) n=length(x); for k=2:n h(k)=x(k)-x(k-1); end for k=2:n l(k)=(y(k)-y(k-1))/h(k); end delt(2)=-h(3)/(2-(h(3)+h(2))); lyam(2)=1.5-(l(3)-l(2))/(h(3)+h(2)); for k=4:n delt(k-1)=-h(k)/(2-(h(k-1)+h(k))+h(k-1)-delt(k-2)); lyam(k-1)=(3-(l(k)-l(k-1))-h(k-1)-delt(k-2))/(2-(h(k -1)+h(k))+h(k-1)-delt(k-2)); end c(n)=0; for k=n:-1:3 c(k-1)=delt(k-1)-c(k)+delt(k-1); end for k=2:n d(k)=(c(k)-c(k-1))/3/h(k); b(k)=l(k)+(2-c(k)-h(k)+h(k)-c(k-1))/3; end end function z=my-spline(x, y, t) % Вычисляет значение кубического сплайна в точке t, % здесь x,y — массивы абсцисс и ординат экспериментальных точек [b, c, d]=koef-spline(x,y); n=length(x); a=y; % определяем j — номер интервала, которому принадлежит точка t. if t>x(n-1) j=n; else for i=2:n-1 if t<=x(i) j=i; break end end end z=a(j)+b(j)-(t-x(j))+c(j)-(t-x(j))^2+d(j)-(t-x(j))^3; end % Экспериментальные точки. U1=[132 140 150 162 170 180]; P0=[330 350 385 425 450 485]; % Точки, в которых надо посчитать ожидаемое значение сплайна. x=[145 155 175]; for i =1:3 % Расчёт ожидаемого значения с помощью функции my-spline. y(i)=my-spline(U1, P0, x(i)); end % Вычисление значений для построения графика сплайна. U2= 132:1:180; for i=1:length(U2) P2(i)=my-spline(U1, P0, U2(i)); end x y % Построение графика. plot(U1,P0, ’*b;experiment;’,U2,P2, ’-r;spline;’, x, y, ’pb;points;’) grid on; % Результаты работы программы x = 145 155 175 y= 373.19 408.77 471.15Листинг 12.5. Решение примера 12.2
| x | 0.298 | 0.303 | 0.31 | 0.317 | 0.323 | 0.33 |
| u | 3.25578 | 3.17639 | 3.1218 | 3.04819 | 2.98755 | 2.9195 |
В следующей задаче воспользуемся встроенными функциями Octave.
Пример 12.3. В результате эксперимента определена функция 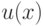 (см. табл. 12.4). Построить график интерполяционной зависимости. Вычислить ожидаемое значение функции при
(см. табл. 12.4). Построить график интерполяционной зависимости. Вычислить ожидаемое значение функции при 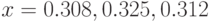 .
.
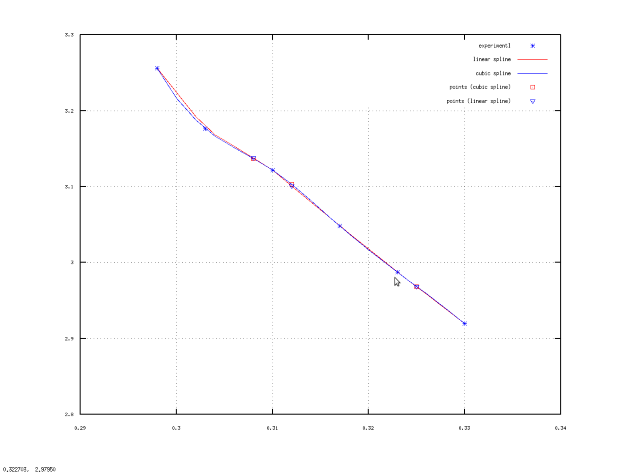
Для решения задачи воспользуемся функцией  . В листинге 12.6 представлено решение примера 12.3, а на рис. 12.3 — графическая иллюстрация.
. В листинге 12.6 представлено решение примера 12.3, а на рис. 12.3 — графическая иллюстрация.
% Экспериментальные точки x =[0.298 0.303 0.31 0.317 0.323 0.33]; u =[3.25578 3.17639 3.1218 3.04819 2.98755 2.9195]; % Точки, в которых надо посчитать ожидаемое значение. x1 =[0.308 0.312 0.325]; % Расчёт значений в точках 0.308, 0.312, 0.325 с помощью кубического сплайна. u1s=interp1(x, u, x1, ’spline’) % Расчёт значений в точках 0.308, 0.312, 0.325 с помощью линейного сплайна. u1l=interp1(x, u, x1, ’linear’) % Вычисление значений для графиков линейного и кубического сплайнов. xi = 0.298:0.002:0.33; uxis=interp1(x, u, xi, ’spline’); uxil=interp1(x, u, xi, ’linear’); % Построение графика plot(x, u, ’*b;experimentl;’, xi, uxil, ’-r;linear spline;’, xi, uxis , ’-b;cubic spline;’, x1, u1s, ’pr;points(cubic spline);’, x1, u1l, ’<b;points(linear spline);’); axis([0.29, 0.34, 2.8, 3.3]); grid on; % Результаты работы программы, u1s = 3.1370 3.1031 2.9685 u1l = 3.1374 3.1008 2.9681Листинг 12.6. Решение примера 12.3
Как и при решении задачи аппроксимации (подбора кривой методом наименьших квадратов), при построении интерполяционных зависимостей, необходимо первоначально поставить и решить задачу с точки зрения математики, и только потом использовать функции пакета Octave.
Этой задачей мы завершаем краткое введение в Octave. В книге были рассмотрены только некоторые функции и методы решения математических и инженерных задач. Далее читатель может самостоятельно продолжить изучение Octave. Официальная страница справки http://www.gnu.org/software/octave/doc/interpreter/. Следует помнить, что существует огромное количество расширений к пакету, описание пакетов расширений приведено на странице http://octave.sourceforge.net.