|
Возможна ли разработка приложения на Octave с GUI? |
Обработка результатов эксперимента. Интерполяция функций
12.2 Интерполяция сплайнами
Рассмотрим один из наиболее распространённых вариантов интерполяции кубическими сплайнами. Было установлено [2], что недеформируемая линейка между соседними углами проходит по линии, удовлетворяющей уравнению
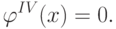 |
( 12.7) |
Функцию
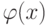
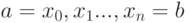
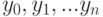
Кубическим сплайном, интерполирующим на отрезке ![[a, b]](/sites/default/files/tex_cache/022022f289db140169cd9514f74ee648.png) данную функцию
данную функцию 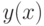 , называется функция [2]
, называется функция [2]
![g_k(s)=a_k+b_k(s-x_k)+c_k(s-x_k)^2+d_k(s-x_k)^3,s\in[x_k-1,x_k],k=1,2,...,n,](/sites/default/files/tex_cache/267c042cc0cfc9984d4c0fa61cc85cb1.png) |
( 12.8) |
удовлетворяющая следующим условиям:
-
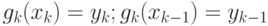 (условие интерполяции в узлах сплайна);
(условие интерполяции в узлах сплайна); - функция
 дважды непрерывно дифференцируема на интервале
дважды непрерывно дифференцируема на интервале ![[a, b]](/sites/default/files/tex_cache/022022f289db140169cd9514f74ee648.png) ;
; - на концах интервала функция
 должна удовлетворять следующим соотношениям
должна удовлетворять следующим соотношениям 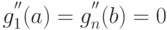 .
.
Для построения интерполяционного сплайна необходимо найти 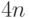 коэффициента
коэффициента 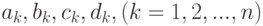
Из определения сплайна получаем  соотношение (12.9)
соотношение (12.9)
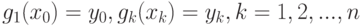 |
( 12.9) |
Из условий гладкой стыковки звеньев сплайна (во внутренних узловых точках совпадают значения двух соседних звеньев
сплайна1Звеном сплайна называется функция 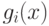 на интервале
на интервале ![[x_{i-1},x_i]](/sites/default/files/tex_cache/ed8b7a028723ab12973db25f831c8ff7.png) , их первые и вторые производные) получаем ещё ряд соотношений (12.10–12.11) [2]:
, их первые и вторые производные) получаем ещё ряд соотношений (12.10–12.11) [2]:
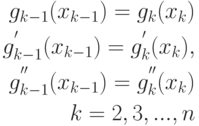 |
( 12.10) |
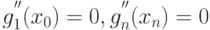 |
( 12.11) |
Соотношения (12.9)–(12.11) образуют 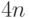 соотношений для нахождения коэффициентов сплайна. Подставляя выражения функций (12.8) и их производных (12.12)
соотношений для нахождения коэффициентов сплайна. Подставляя выражения функций (12.8) и их производных (12.12)
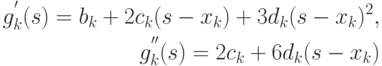 |
( 12.12) |
в соотношения (12.9)–(12.11) и принимая во внимание соотношение
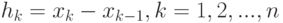 |
( 12.13) |
получим следующую систему уравнений (12.14)–(12.20)
 |
( 12.14) |
 |
( 12.15) |
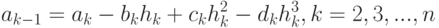 |
( 12.16) |
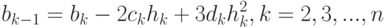 |
( 12.17) |
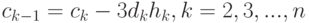 |
( 12.18) |
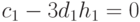 |
( 12.19) |
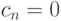 |
( 12.20) |
Задача интерполяции свелась к решению системы (12.14–12.20). Из соотношения (12.15) следует, что все коэффициенты  . Подставив соотношения (12.14), (12.15) в (12.16) и используя фиктивный коэффициент
. Подставив соотношения (12.14), (12.15) в (12.16) и используя фиктивный коэффициент 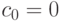 , получим соотношение между
, получим соотношение между 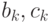 и
и 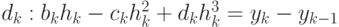
Отсюда коэффициенты b k вычисляются по формуле
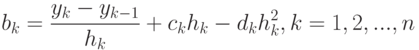 |
( 12.21) |
Из (12.18) и (12.19) выразим 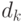 через
через 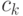 (с учётом коэффициента
(с учётом коэффициента 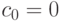 )
)
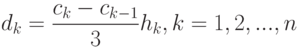 |
( 12.22) |
Подставим (12.22) в (12.21)
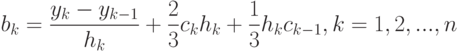 |
( 12.23) |
Введём обозначение
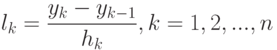 |
( 12.24) |
после чего соотношение (12.23) примет вид:
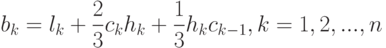 |
( 12.25) |
Подставим (12.25) и (12.22) в соотношение (12.17), получим систему относительно 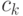
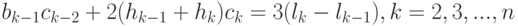 |
( 12.26) |
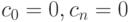 |
( 12.27) |
Систему (12.26) можно решить, используя метод прогонки (http://ru.wikipedia.org/wiki/Метод_прогонки). Этот метод сводится к нахождению прогоночных коэффициентов по формулам прямой прогонки
 |
( 12.28) |
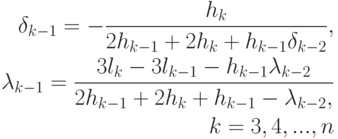 |
( 12.29) |
а затем к нахождению искомых коэффициентов 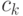 по формулам обратной прогонки
по формулам обратной прогонки
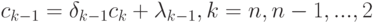 |
( 12.30) |
После нахождения коэффициентов  по формуле (12.30), находим
по формуле (12.30), находим  и
и  по формулам (12.22), (12.25).
по формулам (12.22), (12.25).
Таким образом, алгоритм расчёта коэффициентов интерполяционного сплайна можно свести к следующим шагам.
Шаг 1. Ввод значений табличной зависимости 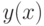 , массивов
, массивов  и
и  .
.
Шаг 2. Расчёт элементов массивов  и
и  по формулам (12.13) и (12.25).
по формулам (12.13) и (12.25).
Шаг 3. Расчёт массивов прогоночных коэффициентов δ и λ по формулам (12.28), (12.29).
Шаг 4. Расчёт массивов коэффициентов  по формуле (12.30).
по формуле (12.30).
Шаг 5. Расчёт массивов коэффициентов  по формуле (12.25).
по формуле (12.25).
Шаг 6. Расчёт массивов коэффициентов  по формуле (12.22).
по формуле (12.22).
После этого в формулу (12.8) можно подставлять любую точку  и вычислять ожидаемое значение.
и вычислять ожидаемое значение.
Расчёт коэффициентов кубического сплайна очень громоздкий и зачастую на практике вместо кубического сплайна используется линейная интерполяция (линейный сплайн). Использование линейного сплайна оправдано в случае, если необходимо просто вычислить значение в определённых точках и нет требования непрерывности производных интерполяционной функции.
В случае линейной интерполяции в качестве сплайна выступает линейная функция
![f_k(s)=a_k+b_ks,s\in[x_{k-1},x_k],k=1,2,...,n,](/sites/default/files/tex_cache/9aab7d57efe51fb71550595f3fa62a93.png) |
( 12.31) |
удовлетворяющая условию интерполяции в узлах сплайна 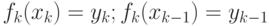 . Коэффициенты
. Коэффициенты  и
и  в этом случае рассчитываются по формулам (12.32), которые получаются из уравнения прямой,проходящей через две точки с координатами
в этом случае рассчитываются по формулам (12.32), которые получаются из уравнения прямой,проходящей через две точки с координатами
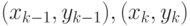
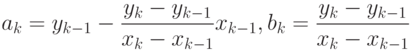 |
( 12.32) |
Найдя коэффициенты линейного сплайна, можно рассчитать значения в любой точке интервала ![[x_0, x_n]](/sites/default/files/tex_cache/4bd054666629869a52d4a028363614c8.png) . Линейная интерполяция даёт достаточно хорошие результаты при практическом счёте внутри интервала
. Линейная интерполяция даёт достаточно хорошие результаты при практическом счёте внутри интервала ![[x_0, x_n]](/sites/default/files/tex_cache/4bd054666629869a52d4a028363614c8.png) , когда от получаемой функции не требуют дополнительных свойств (дифференцируемости и т.д.).
, когда от получаемой функции не требуют дополнительных свойств (дифференцируемости и т.д.).
Напряжение 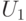 , В , В |
132 | 140 | 150 | 162 | 170 | 180 |
Мощность 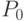 , Вт , Вт |
330 | 350 | 385 | 425 | 450 | 485 |
Рассмотрим реализацию сплайн-интерполяции в Octave. Это можно сделать запрограммировав рассмотренные выше методы сплайн-интерполирования или воспользовавшись функцией , где
, где  — массив абсцисс экспериментальных точек,
— массив абсцисс экспериментальных точек,  — массив ординат экспериментальных точек,
— массив ординат экспериментальных точек,  — точки, в которых необходимо вычислить значение с помощью сплайна,
— точки, в которых необходимо вычислить значение с помощью сплайна, 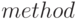 — определяет метод построения сплайна, для реализации сплайн-интерполяции параметр
— определяет метод построения сплайна, для реализации сплайн-интерполяции параметр 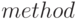 может принимать одно из следующих значений: ’linear’ — линейная интерполяция, ’spline’ — кубический сплайн.
может принимать одно из следующих значений: ’linear’ — линейная интерполяция, ’spline’ — кубический сплайн.
Рассмотрим несколько практических задач.
