|
Возможна ли разработка приложения на Octave с GUI? |
Задачи линейной алгебры
5.6 Решение систем линейных уравнений
Система m уравнений с  неизвестными вида
неизвестными вида

называется системой линейных алгебраических уравнений (СЛАУ), причём  — неизвестные,
— неизвестные,  — коэффициенты при неизвестных,
— коэффициенты при неизвестных, 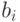 — свободные коэффициенты
— свободные коэффициенты 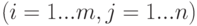 .
.
Кроме того, система из m линейных уравнений с  неизвестными может быть описана при помощи матриц:
неизвестными может быть описана при помощи матриц:  , где
, где 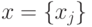 — вектор неизвестных,
— вектор неизвестных, 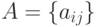 — матрица коэффициентов при неизвестных или матрица системы,
— матрица коэффициентов при неизвестных или матрица системы, 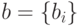 — вектор свободных членов системы или вектор правых частей
— вектор свободных членов системы или вектор правых частей 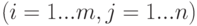 .
.
Матрица  , которая формируется путём приписывания к матрице коэффициентов
, которая формируется путём приписывания к матрице коэффициентов  столбца свободных членов
столбца свободных членов  , называется расширенной матрицей системы.
, называется расширенной матрицей системы.
Если все  , то речь идёт об однородной системе линейных уравнений, иначе говорят о неоднородной системе.
, то речь идёт об однородной системе линейных уравнений, иначе говорят о неоднородной системе.
Совокупность всех решений системы 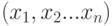 , называется множеством решений или просто решением системы. Две системы уравнений называются эквивалентными, если они имеют одинаковое множество решений.
, называется множеством решений или просто решением системы. Две системы уравнений называются эквивалентными, если они имеют одинаковое множество решений.
Однородные системы линейных уравнений  всегда разрешимы, так как последовательность
всегда разрешимы, так как последовательность 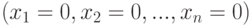 удовлетворяет всем уравнениям системы. Такое решение называют тривиальным. Вопрос о решении однородных систем сводится к вопросу о том, существуют ли кроме тривиального другие, нетривиальные решения.
удовлетворяет всем уравнениям системы. Такое решение называют тривиальным. Вопрос о решении однородных систем сводится к вопросу о том, существуют ли кроме тривиального другие, нетривиальные решения.
Система линейных уравнений может не иметь ни одного решения и тогда она называется несовместной, например, в системе:

левые части уравнений совпадают, а правые различны, поэтому никакие значения  и
и  не могут удовлетворить обоим уравнениям сразу.
не могут удовлетворить обоим уравнениям сразу.
Если же система линейных уравнений обладает решением, то она называется совместной. Совместная система называется определённой, если она обладает одним единственным решением, и неопределённой, если решений больше чем одно. Так, система:

определена и имеет единственное решение  , а система уравнений:
, а система уравнений:
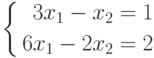
неопределена, так как имеет бесконечное множество решений вида 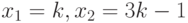 , где число
, где число  произвольно.
произвольно.
Совокупность всех решений неопределённой системы уравнений называется её общим решением, а какое–то одно конкретное решение — частным. Частное решение, полученное из общего при нулевых значениях свободных переменных, называется базисным.
При определении совместности систем уравнений важную роль играет понятие ранга матрицы. Пусть дана матрица  размером
размером 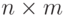 . Вычёркиванием некоторых строк или столбцов из неё можно получить квадратные матрицы
. Вычёркиванием некоторых строк или столбцов из неё можно получить квадратные матрицы  -го порядка, определители которых называются минорами порядка
-го порядка, определители которых называются минорами порядка  матрицы
матрицы  . Наивысший порядок не равных нулю миноров матрицы
. Наивысший порядок не равных нулю миноров матрицы  называют рангом матрицы и обозначают
называют рангом матрицы и обозначают  . Из определения вытекает, что
. Из определения вытекает, что  , а
, а 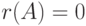 , только если матрица нулевая и
, только если матрица нулевая и  для невырожденной матрицы
для невырожденной матрицы  -го порядка. При элементарных преобразованиях (перестановка строк матрицы, умножение строк на число отличное от нуля и сложение строк) ранг матрицы не изменяется. Итак, если речь идёт об исследовании системы на совместность, следует помнить, что система
-го порядка. При элементарных преобразованиях (перестановка строк матрицы, умножение строк на число отличное от нуля и сложение строк) ранг матрицы не изменяется. Итак, если речь идёт об исследовании системы на совместность, следует помнить, что система  линейных уравнений с
линейных уравнений с  неизвестными:
неизвестными:
- несовместна, если
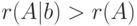 ;
; - совместна, если
 , причём при
, причём при  имеет единственное решение, а при
имеет единственное решение, а при 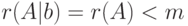 имеет бесконечно много решений.
имеет бесконечно много решений.
Существует немало мето дов для практического отыскания решений систем линейных уравнений. Эти методы разделяют на точные и приближённые. Метод относится к классу точных, если с его помощью можно найти решение в результате конечного числа арифметических и логических операций. В этом разделе на конкретных примерах будут рассмотрены только точные методы решения систем.
Пример 5.8. Решить систему линейных уравнений
 |
( 5.6) |
при помощи правила Крамера.
Правило Крамера заключается в следующем. Если определитель  матрицы системы
матрицы системы  из
из  уравнений с
уравнений с  неизвестными отличен от нуля, то система имеет единственное решение
неизвестными отличен от нуля, то система имеет единственное решение 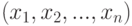 , определяемое по формулам Крамера
, определяемое по формулам Крамера  , где
, где  — определитель матрицы, полученной из матрицы системы
— определитель матрицы, полученной из матрицы системы  заменой
заменой  -го столбца столбцом свободных членов
-го столбца столбцом свободных членов  . Если определитель матрицы системы равен нулю, это не означает, что система не имеет решений: возможно, её нельзя решить по формулам Крамера.
. Если определитель матрицы системы равен нулю, это не означает, что система не имеет решений: возможно, её нельзя решить по формулам Крамера.
Итак, для решения поставленной задачи необходимо выполнить следующие действия:
- представить систему в матричном виде, то есть сформировать матрицу системы
 и вектор правых частей
и вектор правых частей  ;
; - вычислить главный определитель
 ;
; - сформировать вспомогательные матрицы для вычисления определителей
 ;
; - вычислить определители
 ;
; - найти решение системы по формуле
 .
.
Листинг 5.9 содержит решение поставленной задачи.
>>> disp( ’Решение СЛАУ методом Крамера’ ); >>> disp( ’Матрица системы:’ ); A=[2 -1 5; 3 2 -5;1 1 -2] >>> disp( ’Вектор свободных коэффициентов:’ ); b = [ 0; 1; 4 ] >>> disp( ’Главный определитель:’ ); D=det (A) >>> disp( ’Вспомогательные матрицы:’ ); >>> A1=A; A1( :, 1 )=b >>> A2=A; A2( :, 2 )=b >>> A3=A; A3( :, 3 )=b >>> disp( ’Вспомогательные определители:’ ); >>> d( 1 )=det (A1); >>> d( 2 )=det (A2); >>> d( 3 )=det (A3); >>> d >>> disp( ’Вектор решений СЛАУ Ax=b’ ); x=d/D >>> disp( ’Проверка Ax-b=0’ ); A* x’-b % _______________________________ Решение СЛАУ методом Крамера Матрица системы: A = 2 -1 5 3 2 -5 1 1 -2 Вектор свободных коэффициентов: b = 0 1 4 Главный определитель: D = 6 . 0 0 0 0 Вспомогательные матрицы: A1 = 0 -1 5 1 2 -5 4 1 -2 A2 = 2 0 5 3 1 -5 1 4 -2 A3 = 2 -1 0 3 2 1 1 1 4 Вспомогательные определители: d = -17.000 91.000 25.000 Вектор решений СЛАУ Ax=b x = -2.8333 15.166 74.1667 Проверка Ax-b=0 ans = -4.4409e-15 3.5527e-15 8.8818e-16Листинг 5.9. Решение СЛАУ методом Крамера (пример 5.8).
Решение СЛАУ по формулам Крамера выглядит достаточно громоздко, поэтому на практике его используют довольно редко.
Пример 5.9. Решить систему линейных уравнений 5.6 из примера 5.8 методом обратной матрицы.
Метод обратной матрицы: для системы из  линейных уравнений с
линейных уравнений с  неизвестными
неизвестными  , при условии, что определитель матрицы
, при условии, что определитель матрицы  не равен нулю, единственное решение можно представить в виде
не равен нулю, единственное решение можно представить в виде 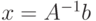 (вывод формулы см. в примере 5.7).
(вывод формулы см. в примере 5.7).
Итак, для того, чтобы решить систему линейных уравнений методом обратной матрицы, необходимо выполнить следующие действия:
- сформировать матрицу коэффициентов и вектор свободных членов заданной системы;
- решить систему, представив вектор неизвестных как произведение матрицы обратной к матрице системы и вектора свободных членов (листинг 5.10).
>>> disp ( ’Решение СЛАУ методом обратной матрицы’ ); >>> disp ( ’Матрица системы:’ ); >>> A=[2 -1 5; 3 2 -5;1 1 -2] >>> disp ( ’Вектор свободных коэффициентов:’ ); >>> b = [ 0; 1; 4 ] >>> disp ( ’Вектор решений СЛАУ Ax=b’ ); >>> x=A^( -1) * b >>> disp ( ’Вектор решений СЛАУ Ax=b с помощью функции inv(A)’ ); >>> x=inv (A) * b >>> disp ( ’Проверка Ax=b’ ); >>> A*x % ______________________________________ Решение СЛАУ методом обратной матрицы Матрица системы: A = 2 -1 5 3 2 -5 1 1 -2 Вектор свободных коэффициентов: b = 0 1 4 Вектор решений СЛАУ Ax=b x = -2.8333 15.1667 4.1667 Вектор решений СЛАУ Ax=b с помощью функции inv(A) x = -2.8333 15.1667 4.1667 Проверка Ax-b=0 ans = -5.3291e-15 1.0000e+00 4.0000e+00Листинг 5.10. Решение СЛАУ примера 5.8 методом обратной матрицы (пример 5.9).
Пример 5.10. Решить систему линейных уравнений
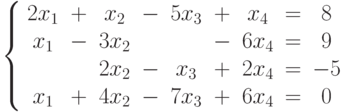 |
( 5.7) |
методом Гаусса.
Решение системы линейных уравнений при помощи метода Гаусса основывается на том, что от заданной системы переходят к эквивалентной системе, которая решается проще, чем исходная система.
Метод Гаусса состоит из двух этапов. Первый этап — это прямой ход, в результате которого расширенная матрица системы путём элементарных преобразований (перестановка уравнений системы, умножение уравнений на число отличное от нуля и сложение уравнений) приводится к ступенчатому виду:

На втором этапе (обратный ход) ступенчатую матрицу преобразовывают так, чтобы в первых n столбцах получилась единичная матрица:

Последний,  столбец этой матрицы содержит решение системы линейных уравнений.
столбец этой матрицы содержит решение системы линейных уравнений.
Исходя из выше изложенного, порядок решения задачи в Octave (листинг 5.11) следующий:
- сформировать матрицу коэффициентов
 и вектор свободных членов
и вектор свободных членов  заданной системы;
заданной системы; - сформировать расширенную матрицу системы, объединив
 и
и  ;
; - используя функцию
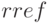 привести расширенную матрицу к ступенчатому виду;
привести расширенную матрицу к ступенчатому виду; - найти решение системы, выделив последний столбец матрицы, полученной в предыдущем пункте;
- выполнить вычисление
 , если в результате получился нулевой вектор, задача решена верно.
, если в результате получился нулевой вектор, задача решена верно.
>>> disp( ’Решение СЛАУ методом Гаусса’ ); >>> disp( ’Матрица системы:’ ); A=[21 - 51; 1 - 30 - 6; 02 - 12; 14 - 76 ] >>> disp( ’Вектор свободных коэффициентов:’ ); b = [ 8; 9; - 5; 0 ] >>> disp( ’Расширенная матрица системы:’ ); C=rref( [A b ] ) >>> disp( ’Размерность матрицы C:’ ); n=size(C) >>> disp( ’Вектор решений СЛАУ Ax=b’ ); x=C( :, n ( 2 ) ) >>> disp( ’Проверка Ax-b’ ); A* x-b % _________________________________ Решение СЛАУ методом Гаусса Матрица системы: A = 2 1 -5 1 1 -3 0 -6 0 2 -1 2 1 4 -7 6 Вектор свободных коэффициентов: b = 8 9 -5 0 Расширенная матрица системы: C = 1.00000 0.00000 0.00000 0.00000 3.00000 0.00000 1.00000 0.00000 0.00000 -4.00000 0.00000 0.00000 1.00000 0.00000 -1.00000 0.00000 0.00000 0.00000 1.00000 1.00000 Размерность матрицы С: n = 4 5 Вектор решений СЛАУ Ax=b x = 3.00000 -4.00000 -1.00000 1.00000 Проверка Ax-b ans = 0.0000e+00 1.7764e-15 -8.8818e -16 -1.6653e -15Листинг 5.11. Решение СЛАУ методом Гаусса (пример 5.10).
Пример 5.11. Решить систему линейных уравнений из примера 5.10 с помощью 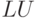 -разложения.
-разложения.
Дадим определение разложения матрицы на множители. Если все определители квадратной матрицы  отличны от нуля, то существуют такие нижняя
отличны от нуля, то существуют такие нижняя  и верхняя
и верхняя  треугольные матрицы, что
треугольные матрицы, что  :
:

Если диагональные элементы одной из матриц ненулевые, то такое разложение единственно.
Метод решения системы линейных уравнений с использованием разложения матрицы коэффициентов на множители называют LU–разложением или LU–факторизацией.
Если матрица  исходной системы
исходной системы  разложена в произведение треугольных матриц
разложена в произведение треугольных матриц  и
и  , то можно записать уравнение:
, то можно записать уравнение: .
.
Введя вектор вспомогательных переменных 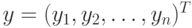 , уравнение
, уравнение  можно переписать в виде системы:
можно переписать в виде системы: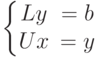 .
.
Таким образом решение системы  с квадратной матрицей коэффициентов свелось к последовательному решению двух систем с треугольными матрицами коэффициентов.
с квадратной матрицей коэффициентов свелось к последовательному решению двух систем с треугольными матрицами коэффициентов.
Обратим внимание на тот факт, что выполнение приведённых расчётов можно интерпретировать как преобразование данной системы к треугольной. Иными словами, LU–разложение это другая схема реализации метода Гаусса.
Исходя из средств, которыми располагает Octave, решение поставленной задачи будет выглядеть так (листинг 5.12):
- сформируем матрицу коэффициентов
 и вектор свободных членов
и вектор свободных членов  заданной системы;
заданной системы; - воспользовавшись функцией
 , получим матрицы
, получим матрицы  (нижняя треугольная матрица),
(нижняя треугольная матрица),  (верхняя треугольная матрица) и
(верхняя треугольная матрица) и  (матрица перестановок или иначе, матрица, которая демонстрирует, каким образом были переставлены строки исходной матрицы при разложении на множители
(матрица перестановок или иначе, матрица, которая демонстрирует, каким образом были переставлены строки исходной матрицы при разложении на множители  и
и  );
); - поскольку в задаче речь идёт о решении системы, то элементы вектора
 должны занять места соответствующие строкам матрицы
должны занять места соответствующие строкам матрицы  , для чего необходимо выполнить действие
, для чего необходимо выполнить действие  ;
; - решим системы уравнений
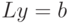 относительно
относительно  ;
; - зная
 и
и  , найдём решение системы
, найдём решение системы  .
.
>>> disp( ’Решение СЛАУ методом LU-разложения’ ); >>> disp( ’Матрица системы:’ ); A=[21 - 51; 1 - 30 - 6; 02 - 12; 14 - 76 ] >>> disp( ’Вектор свободных коэффициентов:’ ); b = [ 8; 9; - 5; 0 ] >>> disp( ’LU-разложение:’ ); [ L, U, P]= lu (A) >>> Y=rref( [ L P* b ] ) >>> n=size(Y) >>> y=Y( :, n ( 2 ) ) >>> X=rref( [U y ] ) >>> n=size(X) >>> x=X( :, n ( 2 ) ) >>> disp( ’Проверка Ax-b’ ); A* x-b % ___________________________________ Решение СЛАУ методом LU-разложения Матрица системы: A = 2 1 -5 1 1 -3 0 -6 0 2 -1 2 1 4 -7 6 Вектор свободных коэффициентов: b = 8 9 -5 0 LU-разложение: L = 1.00000 0.00000 0.00000 0.00000 0.50000 1.00000 0.00000 0.00000 0.50000 -1.00000 1.00000 0.00000 0.00000 -0.57143 -0.21429 1.00000 U = 2.00000 1.00000 -5.00000 1.00000 0.00000 -3.50000 2.50000 -6.50000 0.00000 0.00000 -2.00000 -1.00000 0.00000 0.00000 0.00000 -1.92857 P = Permutation Matrix 1 0 0 0 0 1 0 0 0 0 0 1 0 0 1 0 Y = 1.00000 0.00000 0.00000 0.00000 8.00000 0.00000 1.00000 0.00000 0.00000 5.00000 0.00000 0.00000 1.00000 0.00000 1.00000 0.00000 0.00000 0.00000 1.00000 -1.92857 n = 4 5 y = 8.0000 5.0000 1.0000 -1.9286 X = 1.00000 0.00000 0.00000 0.00000 3.00000 0.00000 1.00000 0.00000 0.00000 -4.00000 0.00000 0.00000 1.00000 0.00000 -1.00000 0.00000 0.00000 0.00000 1.00000 1.00000 n = 4 5 x = 3.0000 -4.0000 -1.0000 1.0000 Проверка Ax-b ans = 0.0000e+00 0.0000e+00 -8.8818e-16 6.6613e-16Листинг 5.12. Решение СЛАУ методом LU-разложения (пример 5.11).
Пример 5.12. Решить систему линейных уравнений

с помощью 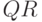 –разложения.
–разложения.
Квадратную матрицу  можно представить в виде произведения ортогональной матрицы
можно представить в виде произведения ортогональной матрицы  и верхней треугольной матрицы
и верхней треугольной матрицы  . Использование этого свойства матриц при решении системы линейных уравнений называют методом QR–разложения.
. Использование этого свойства матриц при решении системы линейных уравнений называют методом QR–разложения.
Идея решения системы этим методом аналогична той, что была описана в предыдущей задаче:
Ax = b -> QRx = b -> (Qy = b, Rx = y).
Таким образом, решение системы уравнений с квадратной матрицей коэффициентов сводится к решению двух систем, матрица коэффициентов первой ортогональная, второй — верхняя треугольная.
Как решить эту задачу средствами Octave, показано в листинге 5.13.
>>> disp ( ’Решение линейной системы с помощью QR–разложения’ ); >>> A=[3,1, -1,2; -5,1,3, -4;2,0,1, -1;1, -5,3, -3] >>> b = [ 6; - 1 2; 1; 3 ] >>> [Q,R]= qr (A) >>> y=Q’ _ b >>> X=rref ( [R y ] ) >>> x=X( 1 : 4, 5 : 5 ) % ____________________________________ Решение линейной системы с помощью QR–разложения A = 3 1 -1 2 -5 1 3 -4 2 0 1 -1 1 -5 3 -3 b = 6 -12 1 3 Q = 0.480384 0.303216 0.358483 0.740797 -0.800641 0.020214 0.545518 0.246932 0.320256 0.070750 0.735670 -0.592638 0.160128 -0.950077 0.180800 0.197546 R = 6.24500 -1.12090 -2.08167 3.36269 0.00000 5.07381 -3.02205 3.30505 0.00000 0.00000 2.55614 -2.74318 0.00000 0.00000 0.00000 0.49386 y = 13.2906 -1.2028 -3.1172 1.4816 X = 1.00000 0.00000 0.00000 0.00000 1.00000 0.00000 1.00000 0.00000 0.00000 -1.00000 0.00000 0.00000 1.00000 0.00000 2.00000 0.00000 0.00000 0.00000 1.00000 3.00000 x = 1.00000 -1.00000 2.00000 3.00000Листинг 5.13. Решение СЛАУ методом QR-разложения (пример 5.12).
Пример 5.13. Исследовать систему на совместность и если возможно решить её:
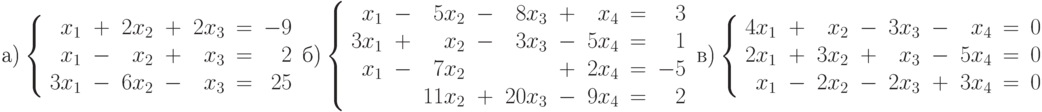
Для решения задачи (листинг 5.14) введём исходные данные, то есть матрицу коэффициентов системы и вектор правых частей. Затем выполним вычисление рангов матрицы коэффициентов и расширенной матрицы системы.
В случае а) ранги матриц равны и совпадают с количеством неизвестных 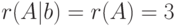 , значит, система совместна и имеет единственное решение. Вычисление рангов матрицы системы и расширенной матрицы системы б) показывает, что ранг расширенной матрицы больше ранга матрицы системы
, значит, система совместна и имеет единственное решение. Вычисление рангов матрицы системы и расширенной матрицы системы б) показывает, что ранг расширенной матрицы больше ранга матрицы системы 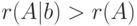 , что означает несовместность системы. В процессе вычислений для системы в) выясняется, что ранг расширенной матрицы равен рангу матрицы системы
, что означает несовместность системы. В процессе вычислений для системы в) выясняется, что ранг расширенной матрицы равен рангу матрицы системы 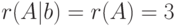 , но меньше, чем количество неизвестных системы
, но меньше, чем количество неизвестных системы 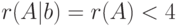 . Значит, система совместна, но имеет бесконечное множество решений.
. Значит, система совместна, но имеет бесконечное множество решений.
disp( ’Исследование системы на совместность’ ); disp( ’Введите матрицу системы:’ ); A=input ( ’A=’ ); disp( ’Введите вектор свободных коэффициентов:’ ); b=input ( ’b=’ ); disp( ’Размерность системы:’ ); [ n,m]= size (A) disp( ’Ранг матрицы системы:’ ); r= rank (A) disp( ’Ранг расширенной матрицы:’ ); R= rank ( [A b ] ) if r==R disp( ’Система совместна.’ ); if r==m disp( ’Система имеет единственное решение.’ ); disp( ’Решение системы методом обратной матрицы:’ ); x=inv (A) _ b disp( ’Проверка Ax-b=0:’ ); A_ x_b else disp( ’Система имеет бесконечно много решений.’ ) end; else disp( ’Система не совместна’ ); end; % Исследование системы а) Исследование системы на совместность Введите матрицу системы: A= [ 1 2 5; 1 -1 3; 3 -6 -1] Введите вектор свободных коэффициентов: b= [ - 9; 2; 25 ] Размерность системы: n = 3 m = 3 Ранг матрицы системы: r = 3 Ранг расширенной матрицы: R = 3 Система совместна. Система имеет единственное решение. Решение системы методом обратной матрицы: x = 2.0000 -3.0000 -1.0000 Проверка Ax-b=0: ans = 0.0000e+00 8.8818e-16 3.5527e-15 % Исследование системы б) Исследование системы на совместность Введите матрицу системы: A= [ 1 -5 -8 1; 3 1 -3 -5;1 0 -7 2; 0 11 20 -9] Введите вектор свободных коэффициентов: b= [ 3; 1; - 5; 2 ] Размерность системы: n = 4 m = 4 Ранг матрицы системы: r = 3 Ранг расширенной матрицы: R = 4 Система не совместна % Исследование системы в) Исследование системы на совместность Введите матрицу системы: A= [ 4 1 -3 -1;2 3 1 -5;1 -2 -2 4 ] Введите вектор свободных коэффициентов: b= [ 0; 0; 0 ] Размерность системы: n = 3 m = 4 Ранг матрицы системы: r = 3 Ранг расширенной матрицы: R = 3 Система совместна. Система имеет бесконечное множество решений.Листинг 5.14. Исследование системы на совместность (пример 5.13).
