Общие сведения, установка

Пример 1.2. Решить квадратное уравнение .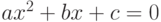

Напомним читателю, что корни квадратного уравнения определяют по формулам 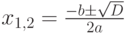, где дискриминант D вычисляется по формуле .

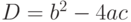В Octave, как и в большинстве математических пакетов, все математические функции определены сразу как для действительных, так и для комплексных чисел, поэтому нет необходимости в тексте программы проверять знак D. Текст программы решения задачи из примера 1.2 приведён в листинге 1.2.

a=input(’a=’); % Ввод значения переменной a.
b=input(’b=’); % Ввод значения переменной b.
c=input(’c=’); % Ввод значения переменной c.
d=b^2-4*a*c; % Вычисление значения дискриминанта.
x1=(-b+sqrt(d))/2/a % Вычисление значения x1.
x2=(-b-sqrt(d))/2/a % Вычисление значения x2.

Для запуска программы на выполнения в окне интерпретатора введём текст:

cd ’/home/evgeniy’
prim1_2

Рис. 1.5. Графики функций y = sin(x), z = cos(x)

Здесь /home/evgeniy — имя папки, где хранится программа, prim1_2.m — имя файла в папке /home/evgeniy, где хранится листинг 1.2.

Далее пользователь должен ввести значение переменных и , после чего появятся результаты работы программы:

	
octave -3.2.3:5 > prim1_2
a=2
b=1
c=1
x1 = -0.25000 + 0.66144i
x2 = -0.25000 - 0.66144i

Пример 1.3. Построить графики функций и 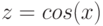на интервале .

Для вычисления значения в Octave есть встроенная функция без параметров 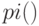. Для построения графика функций и в окне интерпретатора Octave надо ввести следующие команды:

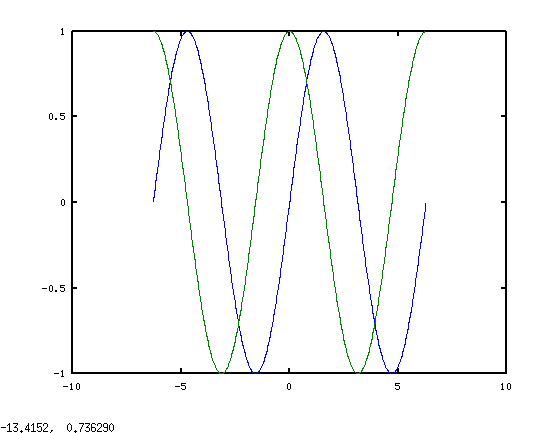
x=-2*pi():0.02:2*pi();
y=sin(x);
z=cos(x);
plot(x,y,x,z)

Результатом работы команд будет графическое окно с графиками двух функций и (см. рис. 1.5).

Как видно из простейших примеров, у Octave достаточно широкие возможности, а по синтаксису он близок к Matlab.

увеличить изображение
Рис. 1.6. Окно Octave Workshop

увеличить изображение
Рис. 1.7. кно QtOctave

Однако для практического использования Octave интерпретатор не совсем удобен, поэтому были разработаны профессиональные графические оболочки для работы с Octave:

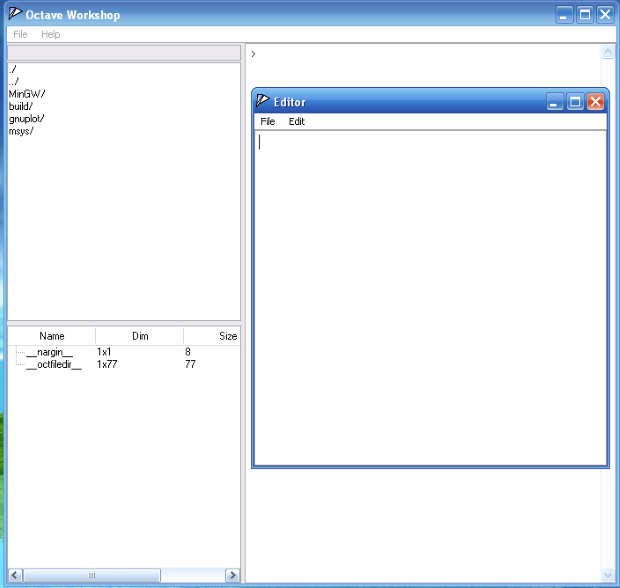
1. Octave workshop (рис. 1.6) — графическая оболочка для работы в ОС Windows.
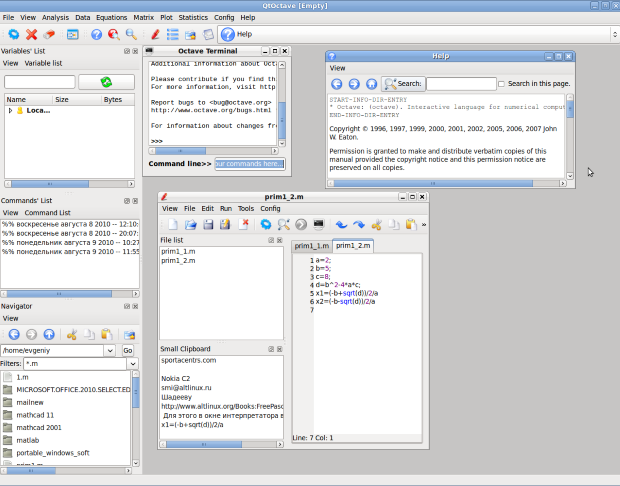
2. QtOctave (рис. 1.7) — графическая оболочка для работы в OC Linux (портирована в ОС Windows в виде portable версии).

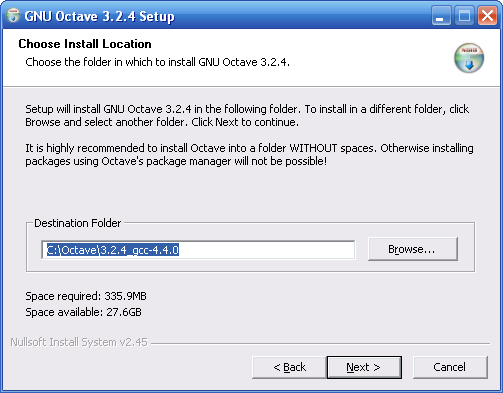
Рассмотрим процесс установки Octave и графических оболочек на персональный компьютер.

Рис. 1.8. Установка Octave. Выбор папки для установки.