Схемотехническая реализация элементов вычислительной техники
Регистр хранения
Регистр – внутреннее запоминающее устройство процессора или внешнего устройства, предназначенное для временного хранения обрабатываемой или управляющей информации. Регистры представляют собой совокупность триггеров, количество которых равняется разрядности регистра, и вспомогательных схем, обеспечивающих выполнение некоторых элементарных операций. Набор этих операций в зависимости от функционального назначения регистра может включать в себя одновременную установку всех разрядов регистра в "0", параллельную или последовательную загрузку регистра, сдвиг содержимого регистра влево или вправо на требуемое число разрядов, управляемую выдачу информации из регистра (обычно используется при работе нескольких схем на общую шину данных) и т.д.
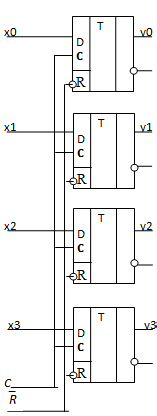
Регистры хранения используются для приема, хранения и выдачи многоразрядого кода. Они представляют собой совокупность одноступенчатых триггеров (как правило, D-типа) с общим входом синхронизации. Иногда в регистре имеется также и общий вход асинхронной установки всех триггеров в "0". Схема четырехразрядного регистра хранения приведена на Рис. 5.15, а его условно-графическое обозначение – на Рис. 5.16.
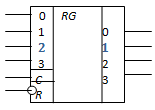
Рис. 5.16. Условно-графическое обозначение четырехразрядного регистра хранения с асинхронным входом установки в "0"
Каждый триггер, ходящий в состав регистра, имеет независимый вход для записи своего разряда числа и общие входы для всех триггерных схем для их синхронизации и установки в "0".
Проектирование многовыходной логической схемы на примере схемы управления JK-триггера
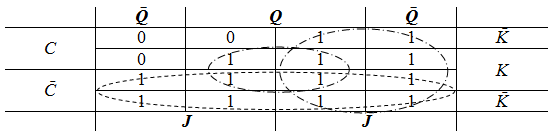
Обобщенная схема синхронного одноступенчатого триггера представлена на Рис. 5.9. Такой триггер состоит из запоминающей ячейки (см. Рис. 5.7) и схемы управления, которая зависит, в общем случае, от входных сигналов данного типа триггера и его состояния в текущий момент времени. Спроектируем такую схему управления для JK-триггера, таблица переходов которого представлена в Табл. 5.10.
Особенностью проектирования данной схемы является то, что здесь на основе одних и тех же входных сигналов необходимо реализовать две различные функции схемы управления запоминающей ячейки: ФАЛ для входа  и ФАЛ для входа
и ФАЛ для входа 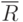 .
.
В общем случае, реализация подобной многовыходной схемы представляет собой нетривиальную задачу, так как часть оборудования, используемого для создания логической функции для одного из выходов, может быть использована также при реализации какой-либо другой функции. Поэтому минимизированная для каждой ФАЛ схема может оказаться не оптимальной с точки зрения для всей многовыходной функции.
В данной лекции мы рассмотрим минимизацию каждой из необходимых функций независимо друг от друга.
Построим таблицу истинности для логических функций  и
и 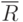 , которые обеспечивают выработку управляющих сигналов на запоминающую ячейку в зависимости от управляющих сигналов J и K, синхросигнала C и состояния запоминающей ячейки Q (Табл. 5.12).
, которые обеспечивают выработку управляющих сигналов на запоминающую ячейку в зависимости от управляющих сигналов J и K, синхросигнала C и состояния запоминающей ячейки Q (Табл. 5.12).
| Входы | Выходы | ||||
|---|---|---|---|---|---|
| C | J | K | Q(t) |  |
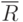 |
| 0 | X | X | X | 1 | 1 |
| 1 | 0 | 0 | X | 1 | 1 |
| 1 | 0 | 1 | X | 1 | 0 |
| 1 | 1 | 0 | X | 0 | 1 |
| 1 | 1 | 1 | 0 | 0 | 1 |
| 1 | 1 | 1 | 1 | 1 | 0 |
Проведем минимизацию с помощью диаграммы Вейча ФАЛ для получения сигнала  :
:
В результате минимизации получим
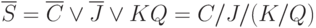
Проведем аналогичную минимизацию для сигнала 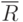 .
.
Получим следующий результат:

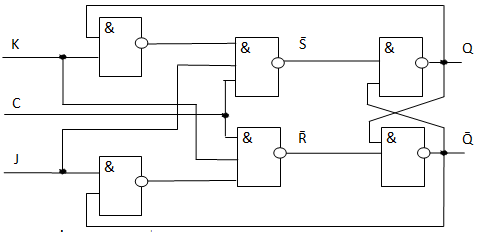
Исходя из полученных уравнений для реализации управляющей схемы запоминающей ячейки, получим следующую схему JK-триггера на элементах "Штрих Шеффера" (Рис. 5.17):
Условно-графическое обозначение этого триггера приведено на Рис. 5.18:
Краткие итоги
В лекции рассматриваются элементы, лежащие в основе различных узлов вычислительной техники. Это как простейшие комбинационные схемы, реализующие элементарные функции алгебры логики, так и более сложные схемы с памятью, на которых базируются триггеры, регистры, счетчики различных типов. Рассмотрен порядок проектирования многовыходных комбинационных схем.
Контрольные вопросы
- Каким образом функции алгебры логики соотносятся с элементами компьютера?
- Соответствует ли система элементов компьютера функционально полному набору логических функций?
- Объясните на схемотехническом уровне работу элемента "И-НЕ".
- Спроектируйте в одноэлементном базисе "И-НЕ" схему, реализующую логическую функцию
 . Необходимо ли для проектирования этой схемы приводить её к совершенному виду?
. Необходимо ли для проектирования этой схемы приводить её к совершенному виду? - Сколько элементов "И-НЕ" потребуется для реализации функции
 ?
? - Чем комбинационные схемы отличаются от последовательностных ?
- Приведите примеры и условные графические обозначения комбинационных схем.
- Расскажите об областях использования комбинационных схем в ЭВМ.
- Сколько выходов имеет дешифратор с восемью входами?
- Какое максимальное количество входов может иметь мультиплексор с четырьмя адресными входами?
- Приведите примеры и условные графические обозначения последовательностных схем
- Почему сдвиговые регистры строят на двух-, а не одноступенчатых триггерах?
- В каких устройствах ЭВМ используются счетчики?
- Нарисуйте схему четырехразрядного регистра хранения на основе RS-триггеров.