Схемотехническая реализация элементов вычислительной техники
Порядок проектирования комбинационных схем в одноэлементном базисе
При проектировании схем, выполняющих ту или иную логическую функцию, необходимо обеспечить минимизацию аппаратных затрат на реализацию этих схем, а также во многих случаях необходимо сократить номенклатуру используемых логических элементов. Последнее требование реализуется путем выбора соответствующей системы элементов. В настоящее время основные серии интегральных логических схем включают в себя элементы, составляющие некоторый функционально полный логический базис, а также дополнительные элементы, реализующие часто встречающиеся логические функции [1]. В качестве функционально полных базисов используются, как правило, одноэлементные базисы "Штрих Шеффера" либо "Стрелка Пирса".
Рассмотрим этапы проектирования комбинационных логических схем на одноэлементном базисе "Штрих Шеффера" без использования каких-либо дополнительных логических элементов на примере проектирования комбинационной схемы pi, выполняющей логическую функцию переноса в следующий разряд при поразрядном суммирования двух операндов (xi и yi) с учетом переноса pi-1 из предыдущего разряда.
Этап 1.Представление функции, выполняемой проектируемой схемой, в каноническом виде, то есть в виде таблицы истинности или одной из совершенных нормальных форм записи. Обычно на этом этапе функцию легче описать таблицей истинности.
Таблица истинности такой схемы приведена ниже (Табл. 5.6).
| Входы | Выход | ||
|---|---|---|---|
| xi | yi | pi-1 | pi |
| 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 0 |
| 0 | 1 | 0 | 0 |
| 0 | 1 | 1 | 1 |
| 1 | 0 | 0 | 0 |
| 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 1 |
Этап 2. Минимизация логической функции. На этом этапе можно использовать любые методы минимизации, описанные выше. Так как значение функции зависит только от трех аргументов, для минимизации удобно использовать метод диаграмм Вейча. Диаграмма Вейча для функции pi представлена на Рис. 5.3.
Минимальная дизъюнктивная нормальная форма для этой функции имеет вид:
pi= xiyi V xipi-1 V yipi-1
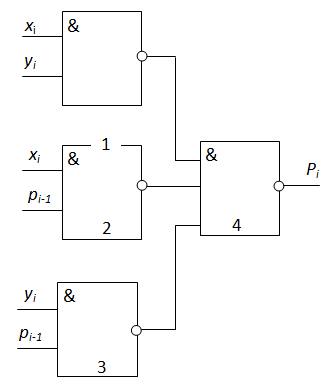
Этап 3. Перевод функции в базис, в котором будет строиться схема. В выбранном варианте это базис "Штрих Шеффера":
Этап 4.Составление схемы на элементах, реализующих функции выбранного базиса. Для более наглядного отображения этого этапа выше обозначены номера элементов, которые будут реализовывать ту или иную часть функции. Полученная схема представлена на Рис. 5.4.
В данной схеме используется одноэлементный комбинационный базис "И-НЕ". Как отмечалось выше, его достаточно для построения схем любой сложности. В то же время, некоторые часто встречающиеся узлы ЭВМ нередко реализуются отдельными микросхемами, фрагментами кристалла программируемых интегральных микросхем (ПЛИС) или отдельными блоками самого микропроцессора.
Прежде всего, отметим, что все элементы компьютера разделяются на комбинационные и последовательностные.
Комбинационными называются элементы, состояние выходов которых зависит только от состояния их входов в текущий момент времени и не зависит от последовательности подачи входных сигналов. Примерами таких элементов являются схемы, реализующие элементарные логические функции, например, элементы, "И-НЕ", которые мы только что использовали.
Последовательностными элементами, или схемами с памятью называются элементы, состояние выходов которых зависит от последовательности подачи входных сигналов. В том числе, и от их текущего состояния.
Сначала рассмотрим некоторые из наиболее часто встречающихся комбинационных схем.