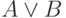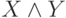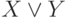Общая теория систем

3.1. Определение и предмет исследования.

Теория — это система средств, позволяющих устанавливать истинность высказываний в заданной области знаний. В аксиоматической теории часть высказываний тождественно истинны (аксиомы, постулаты, гипотезы). В дедуктивной аксиоматической теории имеются правила вывода истинности произвольного высказывания, используя тождественно истинные высказывания (т. е. доказывать теоремы, опираясь на аксиомы). Теория, помимо дедуктивно-аксиоматической, может иметь другую форму: генетическую, гипотетическую и др.; теория может иметь или не иметь формальный аппарат [28, с. 248], [203, 211].

Общая теория систем (ОТС) — это теория, у которой областью знаний являются системы. Структура этой области знаний определяется классификацией систем. Общей частью в этой области знаний являются основные понятия, перечень и последовательность основных стадий, а также отношения между ними. Общее — это то, что присуще всем системам, независимо от их класса, типа, мерности, вида, рода, стадии и т. п. Эта общая часть в системах и составляет предмет исследования общей теории систем. Там, где начинается исследование систем какого-то конкретного класса, типа, мерности, вида, рода, стадии и т. д., там общая теория систем должна переходить в свои разделы, а затем в частные теории, те — в еще более частные и т. д. Таким образом, в области исследования систем должна использоваться иерархическая структура теорий, ниспадающая по убыванию общности и охватывающая все проявления систем. Областью применения такой структуры теорий должна быть вся область системного анализа, ее ромбовидная (рис. 14) и пирамидальная (рис. 16) структуры, которые отражают современный уровень развития теорий по исследованию систем. Естественно, что в этих структурах должна соблюдаться истинность высказываний более общих теорий по отношению к более частным теориям. Истинность высказываний общей теории систем должна соблюдаться во всех теориях и во всех областях исследования систем.

Очевидно, что наше определение ОТС лишь частично совпадает с довольно распространенным определением: "...теория систем есть теория формальных (математических) моделей реально существующих (или концептуальных) систем" [138].

3.2. Метанауки общей теории систем.

Во всякой теории используются совокупности неопределяемых в ней понятий и отношений, считающихся заданными извне, т. е. более общей теорией, наукой или практикой. Для общей теории систем таких наук две: философия, определяющая концептуальную базу, и математика, определяющая формальный аппарат. Мы уже использовали в предыдущих разделах отдельные категории и законы диалектического материализма (единичное — общее — особенное — всеобщее, форма — содержание, количество — качество и др.) и математики (пространства, множества, математический анализ и др.). Рассмотрим отдельные составляющие этих метанаук, которые могут быть использованы в общей теории систем.

* ФИЛОСОФИЯ.

"Предметом диалектического материализма являются наиболее общие законы развития природы, общества и мышления" [74].

Для построения теории философия располагает следующими основными средствами: 1) набором категорий; 2) рядом законов; 3) категориальными структурами; 4) методологией синтеза теории, — объединяемых диалектической логикой.

КАТЕГОРИИ.

"Категории обычно определяются как основные, наиболее общие понятия" [28]. Выделим наиболее общие категории: материя, пространство, время, движение, свойство, единичное — особенное — общее — всеобщее, элемент — состав — структура — система, покой — равновесие — устойчивость, форма — содержание, структура — функция, тождество — различие, основание — условие, возможность — действительность, причина — следствие, случайность — необходимость, явление — сущность, качество — количество и др. [16, 118, 128, 161, 167, 172, 206, 215]. Отметим, что существуют категории единичные (например, пространство), парные (например, возможность действительность) и категории другой кратности. Целостная система категорий или система элементов диалектики отсутствует [154]. Парные категории отражают обычно противоположные качества.

Каждая категория имеет набор признаков, по которым, во-первых, к этой категории можно относить то или иное понятие, и, во-вторых, с помощью этих признаков проводить первичный анализ этого понятия. Например, в паре категорий "причина (п.) — следствие (с.)" в качестве таких признаков можно выделить: главную п., дополнительные п., условия п., общие п., ближайшие п., главное с., дополнительные с., условия с., причинно-следственные взаимодействия (главные, альтернативные, общие, ближайшие, условия).

ЗАКОНЫ.

Закон — это наиболее общие отношения между материальными объектами, явлениями. "Форма всеобщности в природе — это закон..." [129, с. 549].

В философии в качестве основных законов (з.) фигурируют: з. единства и борьбы противоположностей, з. отрицания отрицания, з. перехода количества в качество и наоборот [215].

Закон позволяет устанавливать отношения между категориями, и, следовательно, между понятиями [112].

Каждый закон характеризуется рядом признаков, которые определяют порядок и условия его применения. Например, закон единства и борьбы противоположностей характеризуется: наличием противоречий (п.), внутренними и внешними п., основными и неосновными п., возникновением, обострением и преодолением п., антагонистическими и неантагонистическими п. [194].

КАТЕГОРИАЛЬНЫЕ СТРУКТУРЫ.

Системность категорий и законов философии выражается в форме категориальных структур, позволяющих устанавливать отношения между категориями, и, следовательно, выводить новое знание [154]. Такая структура может устанавливать, скажем, переход одной категории в ее противоположность (из той же пары) на основании критерия — какой-либо третьей категории или одного из законов. Поскольку "третья" категория влечет за собой, обычно, свою противоположность, то может формироваться целая структура категорий и законов. Приведем примеры категориальных структур с координативными (1) и субординативными (2) связями, характерные для теорий классической механики, термодинамики и квантовой механики (рис. 18) [15].

Рис. 18. Примеры категориальных структур (а — ж).

Схема мыслительной деятельности, формирующая связи между локальными категориальными структурами и приводящая к синтезу теории, имеет вид:

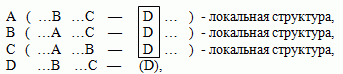
где A, B, C, D - категории; строки - этапы синтеза; категория D задана неявно и характеризует выводимое значение.

МЕТОДОЛОГИЯ СИНТЕЗА ТЕОРИИ [15]

Уточним понятие "теория". Теория - это система (F) средств (положений, понятий, законов, принципов, методов, правил), позволяющих устанавливать истинность высказываний (z) в той или иной области знаний (Z), то есть

(3.1),

где логические знаки : "" - принадлежит, "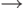" - следует, "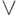" - или, "" - не, "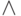" - и.

Исходные предпосылки синтеза теории:

1. Синтез осуществляется на основе развития эмпирических знаний, соответствующих новой предметной области исследований, с использованием предыдущего опыта познания;
2. Синтез происходит через анализ познаний предыдущих теорий и заключается в образовании новых исходных принципов;
3. Для того, чтобы стал возможным синтез фундаментальной теории, недостаточно индуктивных (от частного к общему) методов, ибо он происходит в плоскости аналитико-синтетической деятельности мышления (анализ и синтез).

Для достижения всеобщности теории, ее основные понятия и принципы должны быть независимы (не выводиться один из другого), просты (из минимального количества исходных принципов должно выводиться максимальное количество эмпирических следствий) и непротиворечивы.

Важную роль в получении и обосновании принципов теории играет индукция. Однако индуктивная систематизация ограничена в своих возможностях, так как она предполагает уже готовое знание и не может вывести новое знание.

Другим важным методом построения теории является дедукция. Однако, дедукция не определяет уровня теоретичности знания, а лишь выражает формальные условия этой теоретичности. Метод дедукции оказывается недостаточным для выведения новой теории из старой.

Чтобы синтезировать теорию как систему знания, необходимо осмысливать на основе обобщающей идеи единство многообразия знания. Человек при синтезировании знаний в научную теорию осуществляет аналитическую работу по расчленению при помощи абстракции единого целого. Таким единством является движущаяся материя. Обобщающей идеей в рассматриваемом случае синтеза общей теории систем является ЦЕНТРАЛЬНАЯ ГИПОТЕЗА 1, определяющая понятие "система".

Формой реализации мыслительной деятельности человека, находящей воплощение в синтезе фундаментальной теории, является категориальная структура. Особенность структуры заключается в том, что в ней наряду со связями координации содержатся субординативные связи, благодаря чему она позволяет анализировать процесс развития знания. Выражая эти структуры в соответствующем языке, получим логические схемы (модели) мышления. Категориальные структуры составляют логический каркас, вокруг которого группируются предметные понятия, определяют смысл этих понятий. Поскольку структура означает не простой набор элементов, а целое, образованное взаимосвязанными элементами таким образом, что каждый зависит от другого и может быть тем, чем он является, только благодаря отношениям с другими элементами, постольку знание целого нельзя вывести из знания частей.

Первоначально категории, используемые на эмпирическом уровне исследования, в своей дискретной совокупности выделяют некоторое семантическое поле. При этом они используются либо каждая в отдельности (пространство, время, свойство и т. п.), либо попарно (содержание и форма, необходимость и случайность и т. п.). Связь между ними устанавливается с помощью логических связок (если ... то, и, или, не). Игнорируя субординацию категорий, мы не сможем добраться до сущности реальных объектов.

Схематизация является основанием всякой теории; единственно только очень схематизированное понятие может быть очень простым. Для построения теории необходимо выделение двух видов схем. Первые являются средством реконструкции в мышлении объектов теории, вторые служат для введения в теорию исходных понятий.

При синтезе научных знаний в систему важно различать абстрактные объекты теории и понятия, при помощи которых мы высказываемся об этих объектах. Различный статус абстрактных объектов и понятий в теории определяет различные способы их введения в теорию. Абстрактные объекты вводятся в нее путемпостроения в ходе идеализации и схематизации эмпирического опыта, реконструируя в мышлении реальный объект. В тоже время, как понятия об этих объектах вводятся в теорию путем экспликации их смысла через определения.

В современной науке важной особенностью при введении абстрактных объектов в теорию является единство процессов идеализации, схематизации и интерпретации. Процесс схематизации и идеализации знания характеризуется следующими моментами: 1) вводится на рассмотрение множество фактов или отдельный факт; 2) изучается способ действия, при помощи которого осуществляется абстрагирование существенного от несущественного в исследуемом факте; идеализация условий при построении идеального объекта происходит либо путем идеального перехода, либо через нахождение инвариантов, либо другим способом; 3) задается термин определяемого абстрактного объекта; 4) на некотором языке формулируется условие, которое мы выделили во время схематизации и идеализации факта; относительно этого условия (свойства) все реальные объекты будут находиться в отношении эквивалентности; 5) термин и выделенное условие интерпретируются на графических однородных объектах, которые являются элементами схемы (точки, линии, буквы, слова и т. п.); определяется соответственно понятию (идее построения) способ связи (синтеза) элементов схемы в целое.

Выделив при помощи категориальных структур основные понятия, нужно при этом определить их в рамках обобщающей идеи теории. Определяется объект посредством свойств. Эти свойства обнаруживаются посредством установления отношений данного объекта с другими объектами (например, через взаимодействие).

* МАТЕМАТИКА.

"Никакой достоверности нет в науках там, где нельзя приложить ни одной из математических наук, и в том, что не имеет связи с математикой" (Леонардо да Винчи) [205].

"Хотя разнообразие математических объектов в наше время огромно, сам математический метод остался таким же, каким был всегда: сначала постулируется или молча принимается небольшое число аксиом, а затем путем повторного применения определенных правил (математической логики) строится теория, т. е. совокупность теорем, описывающих свойства и отношения между объектами, удовлетворяющие этим аксиомам" [94].

Какой формальный аппарат должна иметь общая теория систем? Прежде всего необходимо отметить, что диалектическая логика (категории, законы, категориальные структуры, методология синтеза теории), с помощью которой мы уже сформулировали и определили основные понятия и отношения в системном анализе, не является наукой дедуктивной, или индуктивной, или синтетико-аналитической. Она — многогранна. Математические же теории носят дедуктивный характер. Поэтому, формулируя содержательную часть ОТС на базе философии, а формальную часть — на базе математики, мы рискуем никогда не иметь зеркального соответствия между формой и содержанием ОТС, как того требует ромбовидная структура системного анализа. Тем не менее, используя "дырочно-решетчатую" структуру ОТС, мы будем искать математические средства для построения дедуктивной аксиоматической общей теории систем.

Мы уже установили, что использование теории множеств в качестве формальной основы ОТС имеет два принципиальных недостатка: игнорирование целостности системы в качестве базового понятия и нивелирование внутренней сложности элементов. Эти недостатки являются основными причинами, которые делают громоздкими и неудобными для практического использования известные варианты ОТС, которые мы назвали "системными теориями". Вспомним также, что попытки группы ученых под псевдонимом Н. Бурбаки использовать теорию множеств в качестве основы всей математики закончились неудачей , о чем свидетельствует развитие таких новых направлений в математике, как модальная логика, нечеткие множества, топосы [51, 231].

Мы не будем рассматривать исчисление предикатов [78] в качестве возможной формальной основы ОТС, поскольку, во-первых, кванторы общности и существования опираются на представление об объекте, как о множестве, во-вторых, предикатная логика вторгается в сферу частно-научных теорий, теряя при этом необходимую для ОТС общность и дублируя методы этих теорий, которые являются, к тому же, более эффективными и простыми, и, в-третьих, в силу незавершенности этой теории [44].

Остановимся на исчислении высказываний [97], которое является основой всякой теории [82, 160], и имеет необходимый уровень общности [142] для описания ОТС. Затем мы перейдем к функциям алгебры логики — для отображения множества функций систем. От функций алгебры логики мы перейдем к вероятностной логике и к теории вероятностей для отображения вероятностных и статистических свойств систем. Там, где необходимо, мы будем также использовать формальный аппарат частно-научных и междисциплинарных теорий, специально его не излагая, ориентируясь, в общем, на ромбовидную и пирамидальную структуры системного анализа (рис. 14, 16).

В значительной мере справедливо высказывание: "...общая теория систем — это система теорий" [25].

ИСЧИСЛЕНИЕ ВЫСКАЗЫВАНИЙ [131].

Определение 1. Алфавитом алгебры высказываний называется множество А_а.в.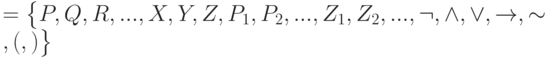, элементы которого называются буквами. Конечные последовательности букв алфавита A_а.в. называются словами в этом алфавите. Некоторые слова в алфавите A_а.в. являются формулами алгебры высказываний.

Определение 2.

(а) P, Q, R, ..., X, Y, Z, P₁, P₂, ..., Z₁, Z₂, ... — формулы.

(б) Если A — формула, то 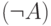— формула.

(в) Если A и B — формулы, то — формулы.

(г) Других формул, кроме перечисленных в пункте (а) и построенных по правилам пунктов (б) и (в), нет.

Формулы, указанные в пункте (а), называются элементарными формулами, или атомами, а полученные по правилам пунктов (б), (в), — сложными формулами, или молекулами.

Определения 1 и 2 составляют синтактику языка логики высказываний.

Рассмотрим семантику букв алфавита алгебры высказываний в классической двузначной логике.

(1) Буквы первой категории — атомы P, Q, R, ..., X, Y, Z, P₁, P₂, ..., Z₁, Z₂, ... . Каждый атом принимает одно из двух возможных истинностных значений: И (истина) или Л (ложь).

(2) Буквы второй категории — логические операторы . Значения этих букв раскрываются в табл. 5, 6, являющихся определениями соответствующих логических операций.

Записи 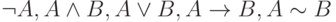читаются, соответственно, "отрицание A", "A конъюнкция B", "A дизъюнкция B", "A импликация B", "A эквиваленция B". В записях 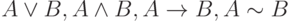формулы A и B называются, соответственно, конъюнктивными, дизъюнктивными, импликативными членами, членами эквиваленции; первый импликативный член A называется антецедентом, второй (B) — консеквентом.

(3) Буквы третьей категории—скобки: левая "(" и правая ")" — играют роль знаков препинания и самостоятельного смысла не имеют.

Рассмотрим истинностные значения и истинностные таблицы формул алгебры высказываний.

Пусть формула A содержит n атомов a₁, ..., a_n. Так как каждый атом может принимать одно из двух возможных истинностных значений И или Л, то различных возможных наборов значений n атомов a₁,...a_n имеется 2ⁿ.

Определение 3. Назовем интерпретацией формулы A алгебры высказываний всякий набор истинностных значений атомов, входящих в формулу A.

Данная формула в конкретной интерпретации сама принимает одно из истинностных значений И или Л, которое определяется при выполнении в требуемом порядке всех предписываемых формулой логических операторов.

Определение 4. Таблица, содержащая всевозможные интерпретации формулы и соответствующие этим интерпретациям значения формулы, называется истинностной таблицей формулы.

Истинностные таблицы строятся по аналогии с табл. 5, 6.

Введем аксиоматическую теорию L исчисления высказываний.

Определение 5. Аксиомами теории L назовем всякие формулы, которые порождают нижеследующие формульные схемы при любом выборе формул A, B, C:

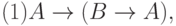
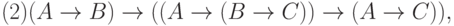
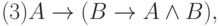
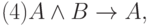
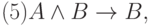
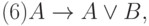
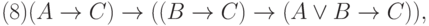
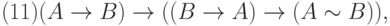
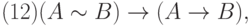
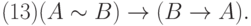
Каждая из схем (1)—(13) порождает счетное множество аксиом, если символы A, B, C заменять конкретными формулами. Поэтому записи (1) — (13) будем называть аксиомными схемами (АС). При этом, АС с двумя формулами носят технический характер интерпретации логических операторов и отношений между ними (записи (1), (3) — (7), (9) — (13)).

Определение 6. Правилом вывода теории L называют процедуру перехода от двух формул вида A и 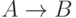к одной формуле вида B для любых A и B.

Это правило называют modus ponens, MP. В случае применения правила MP формулы A и 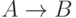называются посылками, а B — заключением этого правила.

Определение 7. Формальным выводом (в теории L) формулы B из посылок A₁, ..., A_n называется конечная последовательность формул B₁, ..., B_k, заканчивающаяся формулой B(B_k=B), причем каждая формула этой последовательности — или одна из посылок, или аксиома, или формула, полученная из некоторых двух предшествующих формул этой последовательности по правилу MP. Если существует формальный вывод формулы B из формул A₁, ..., A_n , то формула B называется формально выводимой из формул A₁, ..., A_n (или теоремой теории L) и это обозначается так: A₁, ..., 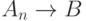, или Г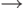B, где Г={A₁, ..., A_n}.

В частном случае, при пустом множестве посылок, формальный вывод называется доказательством.

ФУНКЦИИ АЛГЕБРЫ ЛОГИКИ [131].

В каждой своей интерпретации формула принимает одно из двух истинностных значений — И или Л. Другими словами, формула задает функцию вида {И, Л}ⁿ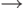{И, Л}.

Определение 8. Функция вида {И, Л}ⁿ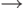{И, Л} называется n-местной истинностной функцией или функцией алгебры логики.

Определение 9. Формулы A и B называются равносильными, если во всех интерпретациях формул A и B, содержащих все атомы формул A и B, истинностные значения этих формул совпадают.

Две равносильные формулы определяют одну и ту же истинностную функцию. Следовательно, истинностные функции можно рассматривать как характеристики классов равносильных формул.

Число n-местных истинностных функций равно .

Обозначим истинностную функцию как f(a₁, ..., a_n), где а₁, ..., а_n — атомы.

Определение 10. Дизъюнкция, составленная из элементарных конъюнкций, называется совершенной дизъюнктивной нормальной формой (СДНФ).

Определение 11. Конъюнкция, составленная из элементарных дизъюнкций, называется совершенной конъюнктивной нормальной формой (СКНФ).

Определение 12. Всякая истинностная функция, не равная тождественно Л, может быть представлена в СДНФ. Всякая истинностная функция, не равная тождественно И, может быть представлена в СКНФ.

Из определения 12 следует, что истинность или ложность функции алгебры логики можно выводить с помощью СКНФ и СДНФ.

Известно, что класс общезначимых (тождественно истинных) формул алгебры логики совпадает с классом доказуемых формул теории L. Поэтому можно доказательства в теории L проводить средствами алгебры логики и наоборот.

ВЕРОЯТНОСТНАЯ ЛОГИКА [46, 184].

Определение 13. Множество М, на котором определены две двуместные операци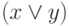и и 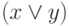и одна одноместная операция и выделены два элемента 0 и , причем для этих операций и элементов выполняются аксиомы (а1)—(а15), называется регулярной булевой алгеброй.

Аксиомы:

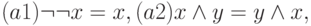
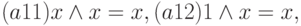
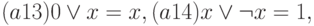
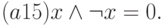
Элементы алгебры логики и булевой алгебры соотносятся: И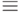1, Л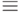0. Определения логических операторов (табл. 5, 6) сохраняются с учетом сложения по модулю 2 (табл. 7).

Назовем элементы регулярной булевой алгебры событиями.

Определение 14. Функция P(x), заданная на М, называется вероятностной мерой (или, просто, вероятностью), если оно удовлетворяет следующим аксиомам:

(1) 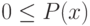для всех ;

(2) P(1)=1;

(3) если 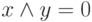, то .

Определение 15. События x и y, у которых 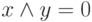, называются несовместимыми.

Определение 16. Пусть a — фиксированный элемент М, причем 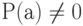. Функция 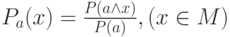называется условной вероятностью события х относительно события а.

Определение 17. Система событий а₁, а₂ ..., аn называется полной системой несовместимых событий, если эти события попарно несовместимы и .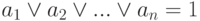

Если булева алгебра М_n=М(а₁, а₂, ..., а_n), то М_n состоит из 2ⁿ элементов, каждый из которых имеет вид f(a₁, a₂, ..., a_n), где f — функция алгебры логики от n переменных, которая может быть представлена в СДНФ и СКНФ.

Зададим значения Р на а_i : Р(а_i)=р_i

Определение 18. Полная система Е несовместимых событий из конечной булевой алгебры М называется системой элементарных событий, если всякое событие из М является дизъюнкцией событий из М.

Для задания вероятности на М достаточно задать ее на элементарных событиях. Задаваемые вероятности должны быть неотрицательны и их сумма должна равняться 1. Других условий нет. Вероятности же элементарных событий задаются, исходя из реальной ситуации.

Определение 19. Пусть на булевой алгебре М задана вероятность Р. Если имеется некоторая конечная полная система несовместимых событий а₁, ..., а_k, и каждому а_i поставлено в соответствие число 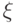(а_i), то будем говорить, что нам задана случайная величина 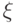. Система событий {а_i} называется характеристической системой событий для .

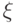МЕТОДИЧЕСКОЕ ПОЯСНЕНИЕ: Каждому событию а_i могут быть, в свою очередь, поставлены в соответствие наборы более элементарных событий. Тогда 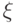может рассматриваться как случайная функция на М, а а_i — как ее структура.

Определение 20. Пусть {а₁, а₂, ..., а_k} — характеристическая система событий случайной величины x. Математическим ожиданием, или средним значением, случайной величины x называется число

.

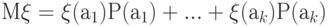МЕТОДИЧЕСКОЕ ПОЯСНЕНИЕ: Нас интересует математическое ожидание как значение случайной функции, а характеристическая система событий — как набор всевозможных структур, на которых эта функция реализуется.

Определение 21. Дисперсией случайной величины 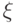называется число

.

МЕТОДИЧЕСКОЕ ПОЯСНЕНИЕ: Нас интересует дисперсия 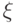с точки зрения разброса значений случайной функции по отношению к ее математическому ожиданию. В форме 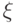, и 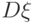мы получили средства, выведенные из исчисления высказываний и алгебры логики, по отношению к которым, однако, мы уже можем, в какой-то мере, использовать аппарат теории вероятностей [30].

АКСИОМАТИЧЕСКИЕ ТЕОРИИ [136, 199, 202].

Аксиоматическая теория в математике понимается как два множества высказываний, из которых одно есть истинное подмножество другого.

Аксиоматическая теория включает а себя: первичные термины; аксиомы, описывающие свойства терминов; логические средства вывода; теоремы, как выводимые новые свойства терминов.

Аксиоматические теории могут быть неформальными и формальными. В формальных теориях первичные термины и вспомогательные средства представляются в форме набора символов некоторого языка; аксиомы формальные выражения операций или отношений символов; средства вывода — формальные средства, например, теории доказательств, включенные в состав теории; теоремы — формальные выражения. В неформальных теориях вместо символов могут использоваться слова, а в качестве средства вывода — внешняя дедуктивная логика философии и математики.

Пример формальной аксиоматической теории — теория L исчисления высказываний. К неформальным аксиоматическим теориям в математике относят, например, теорию групп, аффинную геометрию, частично упорядоченные множества.

Аксиоматическая теория должна быть непротиворечивой и полной. В непротиворечивой теории не могут быть одновременно выведены высказывания A и 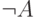. В полной теории для любого высказывания A из заданной области теоремой является либо A, либо .

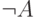Множество аксиом теории называется независимым, если исключение любой аксиомы из этого множества приводит к уменьшению запаса теорем; в противном случае множество аксиом называется зависимым. Добавление в полную, непротиворечивую аксиоматическую теорию, опирающуюся на множество независимых аксиом, дополнительной независимой аксиомы приводит к противоречивости теории [100].