Анализ циклической эволюции систем
10.1. Теория циклической эволюции систем.
Введем понятия простой и циклической эволюции системы. Простая эволюция была нами уже определена (см. рис. 15а) как изменение системы от момента ее возникновения (t0) до момента ее распада  . Исследованы стадии простой эволюции. Циклической эволюцией назовем последовательность простых эволюций системы с заданной функцией (см., например, [64]).
. Исследованы стадии простой эволюции. Циклической эволюцией назовем последовательность простых эволюций системы с заданной функцией (см., например, [64]).
Циклическая эволюция систем (ЦЭС) является продолжением простой эволюции в направлении дальнейшего изменения (повышения или понижения) уровня стационарности и устойчивости системы, в соответствии с ГИПОТЕЗОЙ 6. Поскольку функция системы порождается взаимодействием системы, базы и внешней среды, т.е. структурой внешних отношений (6.9) или (7.1), а определяется внутренней функциональной структурой (6.4'), то повышение уровня ее стационарности и устойчивости зависит как от внешней, так и от внутренней структур системы и проявляется в расширении зоны устойчивости функции. Детализируем отношения (7.1) и (6.4‘) в системном пространстве М:
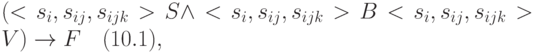
F=F(<si, sij, sijk>г,G) (10.2).
В соответствии с (10.1) функция тем более устойчива, чем больше свойств S, B, V, их характеристик и значений учтено в построении функции. В соответствии с (10.2) функция тем более устойчива, чем на более разнообразные внешние воздействия рассчитана внутренняя функциональная структура системы.
Анализ (10.1) и (10.2) показывает, что стационарность и устойчивость F можно повысить тремя путями (по возрастанию сложности). Перевести из случайного и нестационарного состояния в детерминированное и стационарное как можно больше: 1)значений (sijk) характеристик свойств и отношений между ними; 2)характеристик (sij) свойств и отношений между ними; 3) свойств (si) и отношений между ними.
Первый путь характерен для последовательности ближайших поколений организмов одного вида (изменение значений одних и тех же характеристик) и поколений одного типа искусственных систем (паровоз типа СУ, самолет типа ИЛ-18, цифровая ЭВМ типа МИР и т.п.). Второй путь характерен для длительных последовательностей поколений организмов одного вида (качественные изменения характеристик) и поколений однотипных искусственных систем (паровозы, самолеты, ЦЭВМ и т.п.). Третий путь характерен для разнотипных искусственных систем одного назначения (транспортные системы, системы связи и т.п.)[158].
Целенаправленная циклическая эволюция живых и искусственных систем определяется условиями, которые им обеспечивает Солнечная система и Земля [111]. Для неживых систем, типа Солнечной системы в целом, такие условия или отсутствуют или не имеют значения, или мы о них не имеем представления. Для неживых систем типа атома имеющиеся условия обуславливают их циклическую эволюцию как повторяющуюся последовательность простых эволюций.
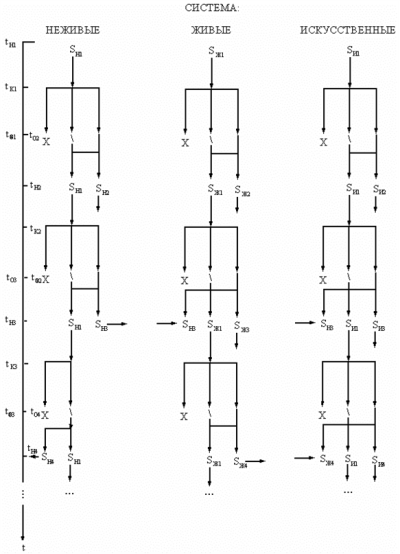
Общая форма циклической эволюции системы - это последовательность ее устойчивых и неустойчивых состояний [77]. При этом, из неустойчивого состояния система может перейти как в новое устойчивое состояние (и продолжать циклическую эволюцию), так и превратиться в другую систему [123], или стабилизироваться на уровне своих частей и элементов, или распасться (потерять системообразующие свойства). Эти переходы имеют ранее рассмотренную условную или безусловную вероятность [152, 222] и могут происходить, в том числе, между различными видами систем (рис. 33).
увеличить изображение
Рис. 33. Схема циклической эволюции систем. Дополнительные обозначения: X -- распад системы; \ -- деградация системы
Например, "...любая реальная биологическая система постоянно переходит от одной точки сохранения к другой, т. е. постоянно решает две задачи: сохранение себя и сохранение своего <рода>" [134].
Способы повышения устойчивости живых и искусственных систем в циклической эволюции: 1) накопление инерционности и механизмов отрицательной обратной связи (у живых систем ѕ в форме генетической памяти, у искусственных систем ѕ в форме научно-технического уровня); 2) создание систем управления; 3) иерархическое построение. Отрицательные обратные связи обеспечивают равновесие не только в организмах, но и в любых системах, как живых, так и неживых. Положительные обратные связи обеспечивают нарушение стабильности [65, 125]. "Закон Бэра: эмбрионы последовательно переходят в своем развитии от общих признаков типа ко все более специальным признакам (класса, отряда, вида, особи)..."[42]. "Общая теория иерархического порядка, очевидно, будет важнейшей составной частью общей теории систем..."[20].
* ЧАСТНЫЙ СЛУЧАЙ.
Повышение устойчивости с помощью отрицательных обратных связей может иметь форму как распределенную по свойствам (самоиндукция -- в электродинамике, кариолисово ускорение -- в механике, регулирование размножения -- в биологии и т.п.), так и целостную, в форме системы управления.
Теория устойчивости автоматических систем управления, имеющих линейный характер (см. выражение (3) примера 1,§8.2), имеет развитый математический аппарат [120]. Устойчивость системы определяется ее внутренней функциональной структурой, т. е. зависит только от характера свободного движения системы. Свободное движение линейной или линеаризованной системы описывается однородным дифференциальным уравнением
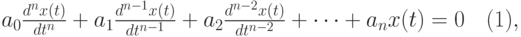
где x(t)=xC(t) -- свободная составляющая выходной величины системы. Вынужденная составляющая выходной величины, зависящая от внешнего воздействия и правой части дифференциального уравнения (3) в примере 1 §8.2, на устойчивость системы не влияет.
Дадим математическое определение понятия "устойчивость". Система является устойчивой, если свободная составляющая xC(t) переходного процесса с течением времени стремится к нулю, т.е. если

Очевидно, что при этом выходная величина системы будет стремиться к вынужденной составляющей, определяемой внешним воздействием и правой частью уравнения (3) примера 1 §8.2. Устойчивость в смысле условия (2) принято называть асимптотической.
Если свободная составляющая неограниченно возрастает, т. е. если
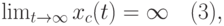
то система неустойчива.
Наконец, если свободная составляющая не стремится ни к нулю, ни к бесконечности, то система находится на границе устойчивости.
Найдем общее условие, при котором система, описываемая уравнением (1), устойчива. Решение уравнения (1) равно сумме
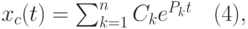
где Ckѕ постоянные, зависящие от начальных условий; pkѕ корни характеристического уравнения
a0p1+a1pn-1+a2pn-2+...+an=0 (5).
Корни характеристического уравнения могут быть действительными (pk=dk), мнимыми 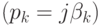 и комплексными
и комплексными

причем комплексные корни всегда попарно сопряжены между собой: если есть корень с положительной мнимой частью, то обязательно существует корень с такой же по модулю, но отрицательной мнимой частью.
Переходная составляющая (4) при  стремится к нулю лишь в том случае, если каждое слагаемое вида
стремится к нулю лишь в том случае, если каждое слагаемое вида  . Характер этой функции времени зависит от вида корня pk. Рассмотрим все возможные случаи расположения корней pk на комплексной плоскости и соответствующие им функции xk(t).
. Характер этой функции времени зависит от вида корня pk. Рассмотрим все возможные случаи расположения корней pk на комплексной плоскости и соответствующие им функции xk(t).
1) Каждому действительному корню  в решении (4) соответствует слагаемое вида
в решении (4) соответствует слагаемое вида
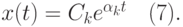
Если 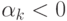 , то функция (7) при
, то функция (7) при  стремится к нулю. Если
стремится к нулю. Если  , то функция (7) неограниченно возрастает. Если
, то функция (7) неограниченно возрастает. Если 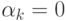 , то эта функция остается постоянной.
, то эта функция остается постоянной.
2) Каждой паре сопряженных комплексных корней  в решении (4) соответствуют два слагаемых, которые могут быть объединены в одно слагаемое
в решении (4) соответствуют два слагаемых, которые могут быть объединены в одно слагаемое

Функция (8) представляет собой синусоиду с частотой 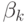 , начальной фазой
, начальной фазой 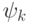 и амплитудой, изменяющейся во времени по экспоненте. Если действительная часть двух комплексных корней
и амплитудой, изменяющейся во времени по экспоненте. Если действительная часть двух комплексных корней 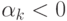 , то колебательная составляющая (8) будет затухать. Если
, то колебательная составляющая (8) будет затухать. Если  , то амплитуда колебаний будет неограниченно возрастать. Наконец, если
, то амплитуда колебаний будет неограниченно возрастать. Наконец, если 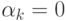 , т.е. если оба сопряженных корня мнимые
, т.е. если оба сопряженных корня мнимые 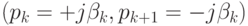 , то xk(t) представляет собой незатухающую синусоиду с частотой
, то xk(t) представляет собой незатухающую синусоиду с частотой 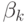 .
.
Если среди корней характеристического уравнения (5) имеются l равных между собой корней pl, то в решении (4) вместо l слагаемых вида  появится одна составляющая
появится одна составляющая
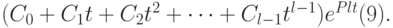
Учитывая, что функция вида e-bt при любом b убывает быстрее, чем возрастают слагаемые вида tr, можно доказать что и в случае кратности корней решение (4) будет стремиться к нулю лишь при отрицательности действительной части кратных корней pl.
На основании проведенного анализа можно сформулировать общее условие устойчивости: для устойчивости линейной автоматической системы управления необходимо и достаточно, чтобы действительные части всех корней характеристического уравнения системы были отрицательными. Если хотя бы один корень имеет положительную действительную часть, то система будет неустойчивой.
В теории автоматического управления разработан ряд правил, с помощью которых можно судить о знаках корней, не решая характеристическое уравнение и не находя числовые значения самих корней. Эти правила называются критериями устойчивости.
При помощи критериев устойчивости можно установить факт устойчивости или неустойчивости системы, все параметры которой заданы. Однако часто при анализе и синтезе систем возникает более общая задача анализа устойчивости - определение допустимых (по условию устойчивости) пределов изменения некоторых параметров системы. В качестве таких варьируемых параметров в ТАУ обычно рассматривают коэффициенты и постоянные времени управляющего устройства, которые можно целенаправленно изменять при синтезе системы. Иногда допустимые пределы изменения определяют и для параметров объекта управления (если последние изменяются при работе системы). Варьируемыми параметрами могут служить также коэффициенты характеристического уравнения, которые, как известно, однозначно связаны с передаточными коэффициентами и постоянными времени элементов САУ.
Допустимые пределы варьирования параметров системы можно определить путем построения областей устойчивости. Областью устойчивости называют область в пространстве варьируемых параметров, каждой точке которой соответствуют только левые корни характеристического уравнения. Область устойчивости выделяет из всех возможных значений варьируемых параметров лишь те значения, при которых система устойчива. Поверхность, ограничивающая область устойчивости, называется границей области устойчивости.
* ТЕОРЕТИЧЕСКИЕ ПОЯСНЕНИЯ.
Теория устойчивости систем в общем случае отсутствует. Обращаясь к схеме внешних отношений системы (рис.10) можно сказать, что целостное увеличение устойчивости системы реализуется через отношения SS, а распределенное - через отношения SB и BS (с базой системы, в пространстве  , в пределах границ G), и через SV и VS (с внешней средой, по границе G).
, в пределах границ G), и через SV и VS (с внешней средой, по границе G).
Однако, изменение системы может быть направлено не только в сторону увеличения устойчивости, но и в сторону ее уменьшения. В этом случае действуют так называемые положительные обратные связи, приводящие к разрушению системы.
Таким образом, циклическую эволюцию можно рассматривать как попеременное превалирование в системе отрицательных (стадия функционирования) и положительных (стадия деградации и распада) обратных связей.