Анализ деградации и распада систем
9.1. Теория деградации и распада систем.
Теория деградации и распада систем (теория ДРС) является развитием теории ОТС применительно к стадии деградации и распада систем (см. рис. 15а). Примером исследования теории ДРС являются системы, функция F которых постепенно теряет свои признаки (на интервале  и полностью исчезает (момент
и полностью исчезает (момент 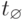 ). При этом основные функциональные характеристики принимают следующие значения:
). При этом основные функциональные характеристики принимают следующие значения:
![\black 1) t=t_k, |F|=M[F]\pm D[F],\quad U_F = f_F =1 (9.1);](/sites/default/files/tex_cache/f061b77528f950286f8e2997f1cf0b04.png)
![\black 2) t_k\leq t\leq t_{\varnothing},\quad |F|\neq M[F]\pm D[F],\quad 0\neq U_F\neq 1, f_F - не определена (9.2);](/sites/default/files/tex_cache/a63865f9fc4fb0db8649581ddc46d7b7.png)
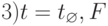 и ее структура |F| отсутствует, UF = fF = 0, (9.3).
и ее структура |F| отсутствует, UF = fF = 0, (9.3).
Состояние распада системы будем обозначать высказыванием  (нефункция). К высказыванию
(нефункция). К высказыванию 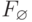 можно применить, в соответствии с гипотезой 6, ту же логику определения, что и к высказыванию F, т.е. использовать схему выделения "несистемы" из внешней среды (рис. 9), при этом "нефункция" порождается взаимодействием системы, базы и внешней среды (6.9). По аналогии с (7.1) "нефункция" порождается отсутствием необходимых свойств, их характеристик и значений, т.е.
можно применить, в соответствии с гипотезой 6, ту же логику определения, что и к высказыванию F, т.е. использовать схему выделения "несистемы" из внешней среды (рис. 9), при этом "нефункция" порождается взаимодействием системы, базы и внешней среды (6.9). По аналогии с (7.1) "нефункция" порождается отсутствием необходимых свойств, их характеристик и значений, т.е.
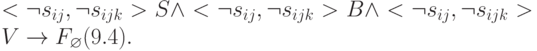
Аналогичным образом можно использовать аппарат алгебры логики и вероятностной логики и вывести (9.1), (9.2), (9.3). При этом мы не будем использовать многозначную и модальную логику, чтобы не загромождать изложение.
Внутренняя функциональная структура 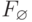 , по аналогии с (6.4), определяется как
, по аналогии с (6.4), определяется как
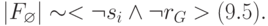
Отметим, что "нефункция" означает отсутствие свойства F у материального объекта N, занимающего часть реального пространства r в границах G.
Вероятностные схемы деградации и распада системы обратны вероятностным схемам возникновения системы (рис. 24), а вероятностные переходы вычисляются аналогично с учетом или без учета условных вероятностей.
Аналогично состояние 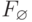 у системы S в терминах теории устойчивости находится в зоне неустойчивости, а в терминах математического программирования — в неоптимальной зоне.
у системы S в терминах теории устойчивости находится в зоне неустойчивости, а в терминах математического программирования — в неоптимальной зоне.
Анализируя зависимости (9.4), (9.5), можно видеть, что к ДРС ведет как нарушение структуры внешних отношений, так и нарушение внутренней функциональной структуры.
* ЧАСТНЫЙ СЛУЧАЙ.
В классической теории динамических систем для анализа нарушений внутренней функциональной структуры (устойчивости) используются вместо линейных дифференциальных уравнений (см. §2.3) нелинейные уравнения со связями типа si1si2, si1si2, (dsi1/dt)(dsi2/dt) и т. п., где sij -- характеристики системы.
