Анализ себестоимости продукции (работ, услуг). Анализ инвестиционных проектов в условиях риска
Пример 2. Провести анализ чувствительности проекта с целью выявления влияния основных исходных факторных показателей на его эффективность. В качестве основного показателя эффективности проекта избрана чистая современная стоимость (NPV). Для анализа чувствительности проекта отобрано пять исходных факторных показателей.
При анализе возможных условий реализации проекта определены минимальные и максимальные границы возможных значений факторных показателей и рассчитаны соответствующие им значения показателя NPV. Минимальные и максимальные границы возможных колебаний каждого из исходных факторных показателей и вызываемых этими колебаниями возможные колебания значений чистой современной стоимости приведены в табл. 6.3.
| Показатель | Границы возможных колебаний исходных факторных показателей, % | Границы возможных отклонений чистой современной стоимости, % | ||
|---|---|---|---|---|
| минимальная | максимальная | минимальная | максимальная | |
| 1 | -15 | +21 | -3 | +6 |
| 2 | -6 | +11 | -5 | +9 |
| 3 | -4 | +12 | -8 | +12 |
| 4 | -16 | +19 | -6 | +10 |
| 5 | -6 | +7 | -3 | +4 |
Исходя из данных таблицы определим диапазон колебаний исходных показателей в процессе реализации проекта. Он составит:
- по первому показателю - 36% (15 + 21);
- по второму показателю - 17% (6 + 11);
- по третьему показателю - 16% (4 + 12);
- по четвертому показателю - 35% (16 + 19);
- по пятому показателю - 13% (6 + 7).
Определим диапазон возможных колебаний чистой современной стоимости в границах предполагаемых изменений исходных показателей. Он составит:
- по первому показателю - 9% (3 + 6);
- по второму показателю - 14% (5 + 9);
- по третьему показателю - 20% (8 + 12);
- по четвертому показателю - 16% (6 + 10);
- по пятому показателю - 7% (3 + 4).
На основе проведенных расчетов определим коэффициент эластичности изменения чистой современной стоимости от изменения каждого из рассматриваемых исходных показателей. Он составит:
- по первому показателю - 0,25% (9 : 36);
- по второму показателю - 0,82% (14 : 17);
- по третьему показателю - 1,25% (20 : 16);
- по четвертому показателю - 0,46% (16 : 35);
- по пятому показателю - 0,54% (7 : 13).
Анализ выполненных расчетов показывает, что наиболее сильное влияние на возможные изменения чистой современной стоимости оказывает третий исходный показатель (коэффициент эластичности больше единицы), а наименьшее - первый исходный показатель (коэффициент эластичности 0,25).
Проект с меньшей чувствительностью NPV считается менее рисковым.
Однако этот метод обладает рядом недостатков, наиболее существенные из них:
- предполагает изменение одного исходного показателя, в то время как остальные считаются постоянными величинами. Однако на практике между показателями существуют взаимосвязи, и изменение одного из них часто приводит к изменениям остальных;
- не позволяет получить вероятностные оценки возможных отклонений исходных и результативного показателей. В этом отношении более предпочтительным является метод сценариев.
Метод сценариев позволяет провести исследование чувствительности результирующего показателя и анализ вероятных оценок его отклонений. Алгоритм анализа инвестиционных рисков данным методом имеет следующий вид:
-
Определяют несколько вариантов изменений ключевых исходных показателей (пессимистический, наиболее вероятный и оптимистический).
-
По каждому варианту изменений устанавливают (экспертным путем) его вероятностную оценку.
-
Для каждого варианта рассчитывают вероятное значение критерия NPV по формуле (6.4).
-
Определяют среднюю величину NPV по формуле
-
Исчисляют стандартное отклонение по формуле
-
Определяют коэффициент вариации (V) по формуле
- Проводится оценка риска проекта.
Для демонстрации техники применения метода сценариев используется следующий пример.
Пример 3. Организация рассматривает инвестиционный проект, связанный с выпуском изделия "А". Полученные в результате опроса экспертов сценарии его развития и возможные вероятности их осуществления приведены в табл. 6.4. Провести анализ риска проекта.
| Показатель | Обозначение показателей | Сценарий | ||
|---|---|---|---|---|
| наихудший, р = 0,25 [1] | вероятный, р = 0,5 | наилучший, р = 0,25 | ||
| Объем выпуска, шт. | Q | 100 | 150 | 200 |
| Цена за штуку, руб. | Ц | 30 | 35 | 40 |
| Переменные расходы, руб. | 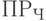 |
25 | 20 | 20 |
| Постоянные затраты, руб. | ПЗ | 200 | 200 | 200 |
| Амортизация, руб. | А | 50 | 50 | 50 |
| Налог на прибыль, % | Н | 24 | 24 | 24 |
| Норма дисконта, % | r | 12 | 10 | 8 |
| Срок проекта, лет | n | 7 | 5 | 5 |
| Начальные инвестиции, руб. | 1С | 2 000 | 2 000 | 2 000 |
| Чистые денежные поступления, руб. |  |
240 | 1 570 | 2 900 |
По данным таблицы определяется значение NPV по вариантам. При этом используется формула расчета современной величины обычной ренты:
-
Исчисляется значение NPV по наихудшему сценарию:
NPV = 240 x 4,564 - 2 000 = -904,6 руб.
-
Исчисляется значение NPV по вероятному сценарию:
NPV = 1 570 x 3,791 - 2 000 = 3 951,9 руб.
-
Исчисляется значение NPV по наилучшему сценарию:
NPV = 2 900 x 3,993 - 2 000 = 9 579,7 руб.
Теперь можно приступить к проведению вероятностного анализа. Прежде всего определяется среднее ожидаемое значение NPV:
 = -904,6 x 0,25 + 3 951,9 x 0,5 + 9 579,7 x 0,25 = 4 144,6 руб.
= -904,6 x 0,25 + 3 951,9 x 0,5 + 9 579,7 x 0,25 = 4 144,6 руб.
Затем исчисляется стандартное (среднее квадратическое) отклонение:
Таким образом, исходя из предположения о нормальном распределении случайной величины с вероятностью около 80% можно утверждать, что значение NPV будет находиться в диапазоне 4 144,6 ± 3 711,82.
Для определения степени риска инвестиционного проекта исчисляется коэффициент вариации:
V = 3 711,8 : 4 144,6 = 0,90.
Полученные результаты в целом свидетельствуют о небольшом уровне риска для данного проекта. Среднее значение NPV (4 144,6) ненамного выше прогноза экспертов (31 711,8. Значение коэффициента вариации (0,90) меньше 1, следовательно, риск данного инвестиционного проекта ниже среднего риска инвестиционного портфеля организации.
В том случае, если значение стандартного отклонения и коэффициента вариации по этому проекту меньше, чем по другим проектам, при прочих равных условиях ему следует отдать предпочтение.
Пример 4. Фирма рассматривает два взаимоисключающих проекта, требующих одинаковых первоначальных инвестиций в 3 600 тыс. руб. и рассчитанных на реализацию в течение 5 лет. Стоимость капитала для фирмы составляет 10%. Менеджеры фирмы определили 3 сценария ежегодных поступлений денежных средств от каждого из проектов. Исходные данные и результаты расчетов приведены ниже.
Проект с большим значением стандартного (среднего квадратического) отклонения и коэффициента вариации считается более рисковым. В приведенном примере (табл. 6.5) более рисковым является проект "Б".
В целом метод сценариев позволяет получить достаточно наглядную картину результатов для различных вариантов реализации проектов. Он обеспечивает менеджера информацией как о чувствительности, так и о возможных отклонениях выбранного критерия эффективности проектов.
Вместе с тем использование данного метода направлено на исследование поведения только результирующих показателей эффективности (NPV, IRR, PI). Метод сценариев не обеспечивает пользователя информацией о возможных отклонениях потоков денежных поступлений и других ключевых показателей, определяющих в конечном итоге ход реализации проекта.
| Показатель | Вероятность осуществления | Проект "А" | Проект "Б" |
|---|---|---|---|
| Инвестиции, тыс. руб. | 3 600 | 3 600 | |
| Ежегодные поступления денежных средств (экспертная оценка): | |||
|
1 000 | 800 | |
|
1 200 | 1 500 | |
|
1 500 | 2 000 | |
| Оценка NPV расчет: | |||
|
0,25 | 191 | -567 |
|
0,5 | 949 | 2 086 |
|
0,25 | 2 086 | 3 982 |
| Среднее, NPV | 1 044 | 1 897 | |
Стандартное отклонение, 
|
680 | 1 774 | |
| Коэффициент вариации, V | 0,65 | 0,94 |
Несмотря на ряд присущих ему ограничений, данный метод успешно применяется во многих разделах финансового анализа.
Анализ вероятностных распределений потоков предполагает возможность определить ожидаемую величину чистых поступлений наличности (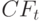 ) в соответствующем периоде, рассчитать по ним чистую современную стоимость (NPV) и оценить ее возможные отклонения. Проект с наименьшей вариацией доходов считается менее рисковым.
) в соответствующем периоде, рассчитать по ним чистую современную стоимость (NPV) и оценить ее возможные отклонения. Проект с наименьшей вариацией доходов считается менее рисковым.
Проблема, однако, заключается в том, что количественная оценка вариации зависит от степени корреляции между отдельными элементами потока платежей. Можно рассмотреть два противоположных случая:
- элементы потока платежей независимы друг от друга во времени, т. е. корреляция между ними отсутствует;
- между элементами потока платежей существует тесная корреляционная связь.
Однако в реальной практике, как правило, между элементами потока платежей обычно существует умеренная корреляция. В этом случае сложность вычислений существенно возрастает, требуются вычислительная техника и специальные программные продукты.
В целом применение изложенного метода анализа рисков позволяет получить информацию об ожидаемых значениях NPV и чистых поступлениях, а также провести анализ их вероятностных распределений.
Но использование этого метода предполагает, что вероятности для всех вариантов денежных поступлений известны либо могут быть точно определены. В действительности распределение вероятностей может быть задано с высокой степенью достоверности только на основе анализа прошлого опыта при наличии больших объемов фактических данных. Однако чаще всего такие данные недоступны, поэтому распределения задаются исходя из предположений экспертов и несут в себе большую долю субъективизма, а расчеты на их основе - большую долю условности.
Деревья решений (decision tree) обычно используются для анализа рисков проектов, имеющих обозримое или разумное число вариантов развития. Они особо полезны в ситуациях, когда решения, принимаемые в момент времени t = n, сильно зависят от решений, принятых ранее, и в свою очередь определяют сценарии дальнейшего развития событий.
Использование данного метода предполагает выполнение следующих последовательных операций:
- для каждого момента времени t определяют проблему и все возможные варианты дальнейших событий;
- откладывают на дереве соответствующую проблеме вершину и исходящие из нее дуги;
- каждой исходящей дуге приписывают ее денежную и вероятностную оценки;
- исходя из значений всех вершин и дуг рассчитывают вероятное значение критерия NPV (либо IRR, PI);
- проводят анализ вероятностных распределений полученных результатов.
Проектам с большей ожидаемой величиной NPV следует отдавать предпочтение.
Следует отметить, что с ростом числа периодов реализации проекта даже при незаметном количестве альтернатив структура дерева сильно усложняется. Быстрый рост сложности вычислений, а также необходимость применения вычислительной техники и специальных программных средств для реализации моделей - основные причины невысокой популярности данного метода оценки рисков на практике. Преодолеть многие недостатки, присущие всем рассмотренным методам, позволяет имитационное моделирование - одно из наиболее мощных средств анализа экономических систем.
Имитация - это компьютерный эксперимент. Отличие его от реального состоит в том, что он проводится с моделью системы, а не с самой системой. Проведение реальных экспериментов с экономическими системами требует значительных затрат и вряд ли осуществимо на практике. Следовательно, имитация - единственный способ исследования систем без осуществления реальных экспериментов.
При решении многих задач финансового анализа используются модели, содержащие случайные величины, поведение которых не поддается управлению (со стороны лиц, принимающих решения). Такие модели называются стохастическими. Применение имитации позволяет сделать выводы о возможных результатах, основанных на вероятностных распределениях случайных факторов. Стохастическую имитацию часто называют методом Монте-Карло.
Имитационное моделирование рисков инвестиционных проектов представляет собой серию численных экспериментов, призванных получать эмпирические оценки степени влияния различных факторов (объема выпуска, цены, переменных расходов и др.) на зависящие от них результаты.
Проведение имитационного эксперимента можно разбить на следующие этапы:
- Установить взаимосвязи между исходными и выходными показателями в виде математического решения уравнения или неравенства.
- Задать законы распределения вероятностей для ключевых параметров модели.
- Провести компьютерную имитацию значений ключевых параметров модели.
- Рассчитать основные характеристики распределений исходных и выходных показателей.
- Провести анализ полученных результатов и принять решение. Результаты имитационного эксперимента могут быть дополнены статистическим анализом, а также использоваться для построения прогнозных моделей и сценариев.
Первый этап анализа согласно сформулированному выше алгоритму состоит в определении зависимости результирующего показателя от исходных данных. При этом в качестве результирующего показателя обычно выступает один из критериев эффективности: NPV, IRR, PI.
Следующий этап проведения анализа состоит в выборе законов распределения вероятностей ключевых переменных величин. При этом можно исходить из предположения, что все ключевые переменные имеют равномерное распределение вероятностей.
Реализация третьего этапа может быть осуществлена только с применением ЭВМ, оснащенной специальными программными средствами.
Технология имитационного моделирования эффективности инвестиционных проектов в среде ППП "Excel" подробно рассмотрена в учебном пособии И.Я. Лукасевича. [2]
Как видно из общей характеристики метода имитационного моделирования, он существенно углубляет аналитический аппарат ранее рассмотренных методов - анализа чувствительности и анализа сценариев проекта. Если метод анализа чувствительности критериев эффективности проекта исследует изолированное влияние каждого из факторных показателей на эффективность, то данный метод, определяя коррелятивную связь между факторными показателями, позволяет исследовать это влияние комплексно. В сравнении с методом анализа сценариев данный метод существенно расширяет исследуемое поле условий реализации проекта, моделируя не 3 возможных сценария, а большее их количество, используя возможности современной компьютерной техники.




