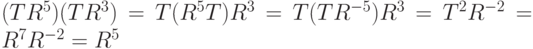Теория групп
На первый взгляд странно, что порядок множителей меняется при обращении произведения. Можно, конечно, сказать, что в данном случае произведение матриц и обращение согласуются с принципом " Носки и Обувь". Утром, когда одеваемся, вначале одеваем носки, а затем одеваем обувь. Вечером все выполняется в обратном порядке, - вначале снимаем обувь, затем снимаем носки.
Справедливость этого порядка можно доказать, умножив обе части этого равенства слева на матрицу (АВ):
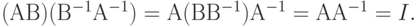
Как мы видели ранее, произведение матриц в общем случае не коммутативно, так что GL(N) - некоммутативная группа.
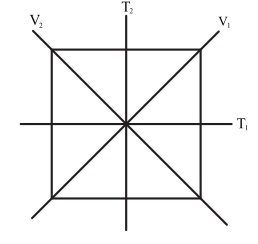
Мы собираемся обсудить наш следующий пример более детально. Рассмотрим группу G трансформаций симметрий квадрата. Есть два типа симметричных преобразований - повороты и отражения. Тождественной трансформацией I при поворотах является поворот на угол в  . Другие повороты - это повороты против часовой стрелки на углы
. Другие повороты - это повороты против часовой стрелки на углы 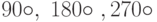 . Обозначим эти повороты соответственно
. Обозначим эти повороты соответственно 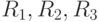 . Группа G содержит также 4 отражения. Два отражения
. Группа G содержит также 4 отражения. Два отражения 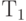 и
и  с осями, проходящими через середины противоположных сторон квадрата, и два отражения
с осями, проходящими через середины противоположных сторон квадрата, и два отражения  и
и 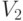 с осями, проходящими через противоположные вершины квадрата (по диагоналям).
с осями, проходящими через противоположные вершины квадрата (по диагоналям).
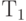 - горизонтальная ось,
- горизонтальная ось,  - вертикальная,
- вертикальная,  - диагональ первого квадранта,
- диагональ первого квадранта, 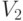 - второго )
- второго )
Будем полагать, что первый базисный вектор  плоскости
плоскости  лежит на оси
лежит на оси 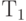 , а вектор
, а вектор  -на оси
-на оси  .
.
Вычислим теперь матрицы, задающие все 8 трансформаций в G:
Мы хотим теперь вычислить таблицу умножения для этой группы. Достаточно просто вычислить произведение поворотов. Понятно, что если выполнить поворот на  , а затем поворот на
, а затем поворот на 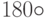 , то результатом этих двух поворотов будет поворот на
, то результатом этих двух поворотов будет поворот на  . Отсюда:
. Отсюда: 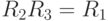 . Это позволяет заполнить четверть таблицы умножения:
. Это позволяет заполнить четверть таблицы умножения:
Далее заметим, что таблица умножения для групп удовлетворяет принципу "Судоку", - ни один элемент таблицы не появляется дважды ни в одной строке и ни в одном столбце. Алгебраическая аргументация такова: если в строке Х появится один и тот же элемент в столбцах У и Z, то это означает, что имеет место равенство: ХУ = Х Z. Умножая обе стороны равенства слева на 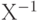 , получим:
, получим:  . Применяя законы ассоциативности, инверсии и тождественности приходим к заключению, что Y=Z, что является противоречием, поскольку все трансформации различны. Следовательно, наша посылка о том, что один и тот же элемент может появляться дважды в строке, ошибочна.
. Применяя законы ассоциативности, инверсии и тождественности приходим к заключению, что Y=Z, что является противоречием, поскольку все трансформации различны. Следовательно, наша посылка о том, что один и тот же элемент может появляться дважды в строке, ошибочна.
Так как элементы не могут повторяться, то каждая строка и столбец должны содержать все элементы группы. Из этого следует, что нижний левый и верхний правый углы таблицы умножения должны быть заполнены отражениями, а нижний правый угол должен содержать повороты.
Следовательно, произведение двух поворотов дает поворот. Произведение поворота и отражения независимо от порядка дает отражение. Произведение двух отражений дает поворот.
Достаточно просто заполнить первый столбец и первую строку, поскольку множителем является тождественный элемент. Мы также знаем, что отражение, примененное дважды, дает тождественный результат. Заметим также, что матрица 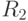 это -I. Будучи поворотом на
это -I. Будучи поворотом на 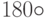 , она трансформирует каждый вектор в его противоположность. Так как умножение на - I означает замену знаков у всех элементов на противоположный знак независимо от порядка умножения, то результаты достаточно просто вычислить. Запишем их:
, она трансформирует каждый вектор в его противоположность. Так как умножение на - I означает замену знаков у всех элементов на противоположный знак независимо от порядка умножения, то результаты достаточно просто вычислить. Запишем их:
Вычислим теперь 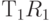 и
и 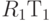 :
:
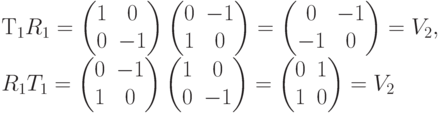
Это показывает, что группа симметрий квадрата не коммутативна! Поместим вычисленные значения в таблицу:
Затем, используя принцип Судоку, заполним часть клеток таблицы умножения: 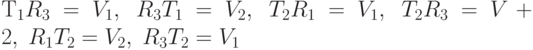 .
.
Мы можем вычислить 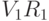 и
и 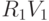 , используя ассоциативный закон:
, используя ассоциативный закон:
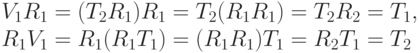
Заполним остаток пустующих клеток двух углов таблицы:
Оставим заполнение клеток последнего угла таблицы в качестве упражнения.
Некоторые группы, которые нам хотелось бы изучать могут быть очень большими. Например, число элементов одной важной группы, называемой " Монстр", равно:
808,017,424,794,512,875,886,459,904,961,710,757,005,754,368,000,000,000.
Если бы мы решили заполнить таблицу умножения для этой группы, то нам бы не хватило чернил, так как число элементов таблицы превосходит число атомов видимой нам Вселенной.
Мы хотим разработать более эффективный и более алгебраический метод для проведения вычислений в группе.
Давайте обобщим наш предыдущий пример и рассмотрим группу симметрий 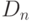 правильного многоугольника с n вершинами. Эта группа называется диедральной группой. Нетрудно видеть, что эта группа имеет n поворотов (на углы, кратные
правильного многоугольника с n вершинами. Эта группа называется диедральной группой. Нетрудно видеть, что эта группа имеет n поворотов (на углы, кратные 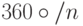 ) и n отражений. Будем обозначать поворот против часовой стрелки на угол
) и n отражений. Будем обозначать поворот против часовой стрелки на угол 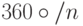 через R. Зафиксируем одно из отражений и назовем его Т. Все повороты в диедральной группе могут быть представлены как степени R:
через R. Зафиксируем одно из отражений и назовем его Т. Все повороты в диедральной группе могут быть представлены как степени R: 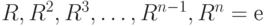 . Последний поворот
. Последний поворот 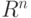 равен е. Та же аргументация, которую мы использовали в случае квадрата, показывает, что произведение отражения и поворота дает отражение. В соответствие с принципом Судоку все отражения
равен е. Та же аргументация, которую мы использовали в случае квадрата, показывает, что произведение отражения и поворота дает отражение. В соответствие с принципом Судоку все отражения 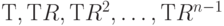 различны и, следовательно, задают все отражения в диедральной группе
различны и, следовательно, задают все отражения в диедральной группе 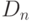 .
.
Это позволяет нам перечислить все элементы диедральной группы следующим образом:
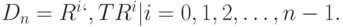
Отметим два равенства: 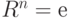 и
и  . Так как произведение
. Так как произведение 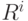 и Т является отражением, то квадрат этого произведения, будучи квадратом отражения, равен тождественному элементу:
и Т является отражением, то квадрат этого произведения, будучи квадратом отражения, равен тождественному элементу: 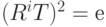 . Отсюда следует, что произведение
. Отсюда следует, что произведение 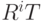 совпадает со своим обращением:
совпадает со своим обращением: 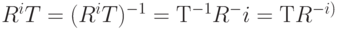 . Полученные три отношения:
. Полученные три отношения:
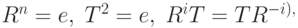
позволяют умножать любые два элемента диедральной группы. Для примера давайте вычислим в группе 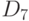 произведение
произведение 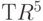 и
и 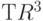 :
: