Системы компьютерной математики (СКМ)
12.5. Графические средства СКМ МathCad
Для создания графиков в среде MathCad имеется встроенный программный инструмент – графический процессор (см. рис.12.2.).
Возможности среды MathCad здесь впечатляют и могут удовлетворить любые, самые взыскательные требования пользователя, или лучше так – можно с уверенностью сказать, что среда МathСad удовлетворит не только любую прихоть пользователя, но, в свою очередь, сможет предложить ему инструмент, о существовании которого тот вряд ли догадывается.
Приятно удивляет простота применения, что позволяет использовать графики не только как средство иллюстрации, но и как удобный инструмент вычислений, постоянно готовый к текущему отображению промежуточных результатов.
На рис.12.7 приведена палитра(панель инструментов) меню Graph для отрисовки графиков, а в таблице 12.4 – назначение и возможности каждого инструмента.
Кроме инструментов, приведенных в таблице 12.4, есть еще два, которые не приведены в палитре рис.12.7. Первый – мастер построения трехмерных графиков (3D Plot Wizard) – вызывается из главного меню (Insert/Graph/3D Plot Wizard) и существенно облегчает форматирование трехмерных графиков.
Второй – окно форматирования рисунка с графиком – вызывается двойным левым щелчком на поле графика или из контекстного меню (КМ). Вид этого окна зависит от типа графика, оно содержит до 9 вкладок и позволяет выполнять с графиком любые манипуляции. Вот некоторые из них:
- форматирование шкалы графика – задание масштаба (в том числе логарифмического), пределов изменения переменных, особенности изображения линий координатной сетки, а то и вовсе – убрать все оси и линии, кроме самого графика (чтобы получить отдельную картинку);
- форматирование линии графика;
- создание заголовков и подписей на осях СК;
- задание по умолчанию параметров рисунка с графиком.
Для примера приведем последовательность действий при построении графика функции
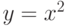 на интервале (-2, 2)
на интервале (-2, 2)
- Введем определение функции
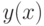 .
. - Вызовем из палитры Graph инструмент X-E Plot.
-
Все будет выполнено автоматически после задания диапазона изменения
 и указания функции на левом знакоместе шаблона:
и указания функции на левом знакоместе шаблона: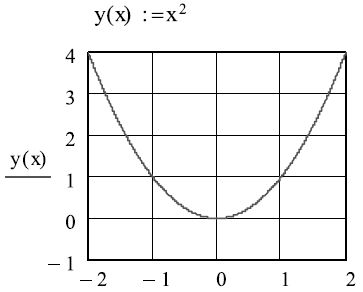
- При необходимости легко изменить диапазон как аргумента так и функции указанием нужных значений на соответствующих знакоместах.
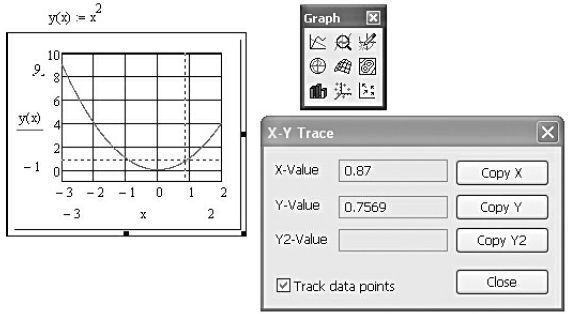
Выполним трассировку графика – указание нужной точки графика: в нашем случае пусть это будет минимум функции 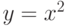 .
.
- Выберем на палитре Graph инструмент Х-У Trace – откроется окно диалога, а на графике появится управляемый мышью указатель.
- Установим опцию Track Data Point, в этом случае перекрестие указателя будет скользить только по кривой графика.
- Скопируем координаты текущей позиции указателя в буфер.
Указанные действия иллюстрирует рис.12.8.
Теперь построим график такой функции двух переменных:
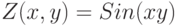
-
Определим функцию z(x,y).
-
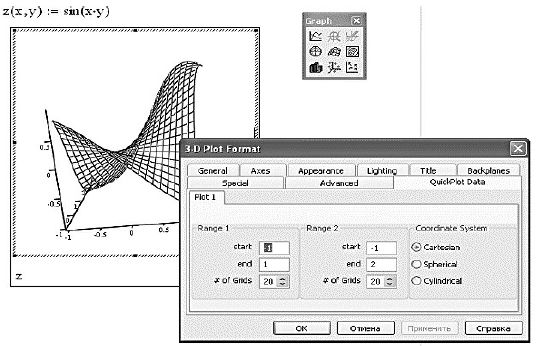
Вызовем из палитры "Graph" инструмент Surface Plot и поместим на нижнем знакоместе только имя функции теперь уже без указания аргументов (см. рис.12.9).
-
Получилось что-то непонятное. Уменьшим диапазон по осям аргументов в четыре раза, для чего вызовем из КМ окно свойств, как показано на рис.12.10.
-
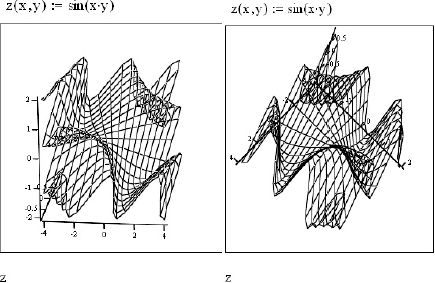
Теперь получилось подозрительно просто – опять увеличим эти диапазоны, а еще захватим график мышью и покрутим его в разные стороны; окончательно получим следующее (см. рис.12.11).
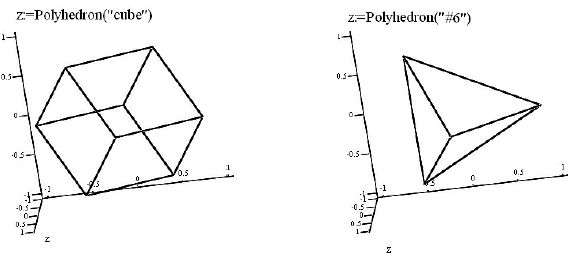
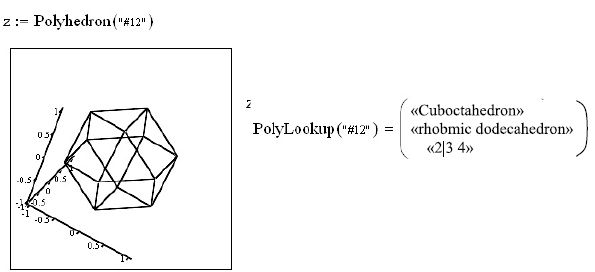
Еще одной изящной возможностью среды можно полюбоваться, снова запустив шаблон 3D графика и вызвав из главного меню (Insert/ Graph/3D Plot Wizard) функцию Polyhedron() – как это показано на рис.12.12, она позволяет изобразить один из 80-ти многогранников (подробные сведения о них приводятся в справочной системе МathСad):
 ,
,
где 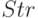 – аргумент в виде управляющей строки, которая в двойных кавычках содержит название многогранника ("cube" – куб), либо его порядковый номер ("#6" – тетраэдр). Все эти порядковые номера можно легко найти в справочной системе MathCad.
– аргумент в виде управляющей строки, которая в двойных кавычках содержит название многогранника ("cube" – куб), либо его порядковый номер ("#6" – тетраэдр). Все эти порядковые номера можно легко найти в справочной системе MathCad.
А желаете узнать, как по-английски правильно называется многогранник, составленный из шести квадратов и восьми треугольников? Взгляните на рис.12.13– там все очевидно.
В заключение упомянем о возможности вставить в разрабатываемый документ анимацию – как при помощи команды Tools/Animation, открывающей окно создания и просмотра анимации, так и путем включения встроенного видеопроигрывателя View/Playback для просмотра любых внешних файлов в формате AVI.