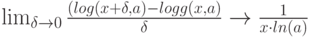НОУ ИНТУИТ | Введение в программные системы и их разработку. Лекция 12: Системы компьютерной математики (СКМ)

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

Национальный исследовательский университет "Высшая Школа Экономики"

Опубликован: 19.11.2012 | Доступ: свободный | Студентов: 2294 / 554 | Длительность: 30:21:00

Темы: Программное обеспечение, Образование

Специальности: Менеджер, Преподаватель

Теги: microsoft word, базы данных, офисные приложения, презентации, программирование

|

Вам нравится? Нравится 23 студентам

| Поделиться |

Поддержать курс

| Скачать электронную книгу

12.4.Символьные расчеты в СКМ

Символьные расчеты выполняются во встроенном символьном процессоре путем вызова нужного оператора с панели инструментов Symbolic (либо при помощи главного меню).

Запуск на выполнение символьных действий выполняется при помощи оператора вывода $\to$ и нажатия клавиши Enter. Результат получается, соответственно, в символьной форме.

Примеры простых символьных расчетов:

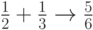
$\sqrt{27} \to 3\cdot \sqrt{3}$ $\frac{1}{2}+\frac{1}{3} \to \frac{5}{6}$

Результат здесь получился в таком же виде, как если бы мы выполняли действия вручную – с корнями, или в виде обыкновенной дроби. При выполнении численных расчетов (оператор = на панели "Calculator") результат будет таким:

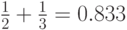
$\sqrt{27} =5.196$ $\frac{1}{2}+\frac{1}{3} =0.833$

Вводим теперь классическое соотношение:

$sin(x)^2+cos(x)^2 \to cos(x)^2+sin(x)^2$

и с удивлением обнаруживаем, что ничего не получилось. А, собственно, чего еще можно было ожидать, даже не задав СКМ своих требований. Для этого используются специальные операторы с панели Symbolic. С их помощью и выполняются все упрощения математических выражений и алгебраические преобразования. Наиболее универсальный из этих операторов – simplify (упростить).

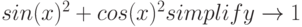
$sin(x)^2+cos(x)^2 simplify \to 1$

Интересно сравнить результаты решения одного и того же, например, квадратного уравнения в символьной форме:

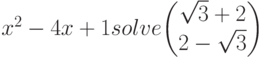
$x^2-4x+1 solve $$\begin{pmatrix} \sqrt{3}+2\\ 2-\sqrt{3} \end{pmatrix}$$$

и в численном виде:

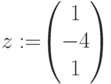
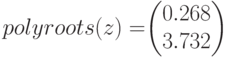
$z:=$$\begin{pmatrix} 1\\ -4\\ 1 \end{pmatrix}$$$ $polyroots (z)=$$\begin{pmatrix} 0.268\\ 3.732 \end{pmatrix}$$$

Во втором случае полином задается вектором коэффициентов , а функция polyroots(z) вычисляет его корни.

Покажем, как выполняются алгебраические преобразования при упрощении математических выражений с помощью других операторов палитры Symbolic (напомним: они вызываются однократным кликом после набора исходного выражения).

Первый пример: оператор expend (разложить), выполняющий перемножение и представляющий результат в виде многочлена. Выполним пример в пошаговом режиме.

Ввести исходное выражение (его можно скопировать как фрагмент из другого выражения).
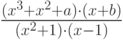
$\frac {(x^3+x^2+a)\cdot(x+b)}{(x^2+1)\cdot(x-1)}$
На палитре Symbolic "кликнуть" на слове expend (разложить) и нажать клавишу Enter.

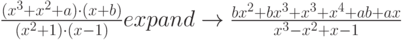
$\frac {(x^3+x^2+a)\cdot(x+b)}{(x^2+1)\cdot(x-1)} expand \to \frac {bx^2+bx^3+x^3+x^4+ab+ax}{x^3-x^2+x-1}$

Выполнилось разложение исходного выражения путем перемножения в числителе и знаменателе. Очень эффектно оператор expend работает в качестве справочного инструмента как показано ниже.

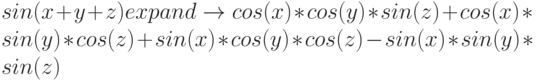
$sin(x+y+z) expand \to cos(x)*cos(y)*sin(z)+cos(x)*sin(y)*cos(z)+sin(x)*cos(y)*cos(z)-sin(x)*sin(y)*sin(z)$

Другой пример

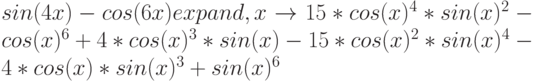
$sin(4x)-cos(6x) expand,x \to 15*cos(x)^4*sin(x)^2-cos(x)^6+4*cos(x)^3*sin(x)-15*cos(x)^2*sin(x)^4-4*cos(x)*sin(x)^3+sin(x)^6$

При помощи оператора factor выполняется разложение на множители, например:

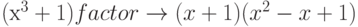
$(х^3+1) factor \to (x+1)(x^2-x+1)$

А вот как можно проверить, является ли число 199995 простым, – выполняем:

$199995 factor \to 3 \cdot 5 \cdot 67 \cdot 199$

убеждаемся, что это число непростое, поскольку в его разложении нашлись четыре простых множителя. А вот так можно привести выражение к общему знаменателю:

$\frac{z}{x-1} + \frac{y}{x+1} factor \to \frac{z-y+xy+xz}{(x-1)(x+1)}$

Оператор collect, наоборот, выносит за скобку общий множитель (через запятую нужно обязательно указать его вид):

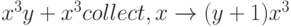
$x^3y+x^3 collect,x \to (y+1)x^3$

Однако, несмотря на кажущуюся простоту, это действие (вынесение множителя) является очень сложной интеллектуальной задачей, поэтому оператор collect работает нечетко, требует подсказки – что нужно выносить, и используется достаточно редко.

А вот оператор разложения на элементарные дроби parfrac и работает отлично, и используется широко; особенно он полезен при интегрировании рациональной функции.

$\frac{5x-1}{(x-1)(x+1)} parfrac \to \frac{2}{x-1} +\frac{3}{x+1}$

Теперь проинтегрировать правую часть не составит труда, если вспомнить, что первообразной для (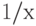 1/х ) является ln(x) .

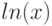Часто при решении математических задач возникает необходимость замены переменной в формуле на заданное выражение. Запишем, например, такую формулу:

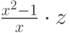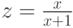
$\frac{x^2-1}{x} \cdot z$ , где $z=\frac{x}{x+1}$

вызовем оператор substitute (заместить) c панели Symbolic

$\frac{x^2-1}{x} \cdot z substitute, \blacksquare=\blacksquare \to$

и в правый маркер (черный квадратик) поместим такую запись, задающую подстановку:

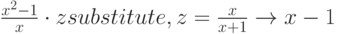
$\frac{x^2-1}{x} \cdot z substitute, z=\frac{x}{x+1} \to x-1$

Как видно, программа не только выполнила требуемую подстановку, но и упростила выражение.

К подстановкам часто приходится прибегать при работе с MathCad и вот почему. Эффективность, например, решения уравнений или действие оператора разложения expend резко повышается, если исходная формула не содержит радикалов (корней).

MathCad постоянно совершенствуется – два классических примера бессилия MathCad 12 [3 ]:

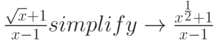
$\frac{\sqrt{x}+1}{x-1} simplify \to \frac{x^{\frac{1}{2}}+1}{x-1}$

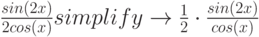
$\frac{sin(2x)}{2cos(x)} simplify \to \frac{1}{2} \cdot \frac{sin(2x)}{cos(x)}$

в MathCad 14 решаются легко:

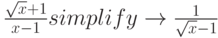
$\frac{\sqrt{x}+1}{x-1} simplify \to \frac{1}{\sqrt{x}-1}$

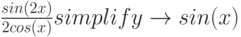
$\frac{sin(2x)}{2cos(x)} simplify \to sin(x)$

Часто на практике требуется выполнить одновременно несколько последовательных преобразований формулы с целью ее упрощения. Для этого служит оператор simplify ("упростить"). Можно сказать, что с его помощью выполняется, в некотором смысле, комплексное упрощение. Оттого он и наиболее востребован.

Например:

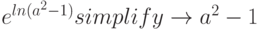
$e^{ln(a^2-1)} simplify \to a^2-1$

Вычисление пределов в среде MathCad отработано надежно и фундаментально, поскольку пределы – основа математического анализа. Про первый замечательный можно даже и не говорить – идеально. Равно как и второй.

С правилом Лопиталя СКМ справляется без проблем:

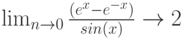
$\lim_{n \to 0} \frac{(e^x-e^{-x})}{sin(x)} \to 2$

И переходить к пределу логарифма с последующим потенцированием среда MathCad тоже умеет:

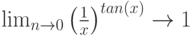
$\lim_{n \to 0} \left(\frac{1}{x} \right) ^{tan(x)} \to 1$

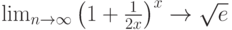
$\lim_{n \to \infty} \left( 1+\frac{1}{2x} \right) ^{x} \to \sqrt{e}$

Могут быть вычислены и односторонние пределы. В следующем хрестоматийном [1] примере предел функции:

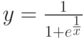
$y=\frac{1}{1+e^{\frac{1}{x}}}$

в точке 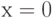х=0 не существует,

$\lim_{n \to 0} \frac{1}{1+e^{\frac{1}{x}}} \to undefined$

тогда как односторонние могут быть определены. Что с успехом и выполняет MathCad .

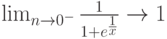
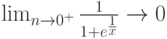
$\lim_{n \to 0^-} \frac{1}{1+e^{\frac{1}{x}}} \to 1$ $\lim_{n \to 0^+} \frac{1}{1+e^{\frac{1}{x}}} \to 0$

Рассмотрим несколько изящных примеров, показывающих возможности вычисления пределов и одновременно красиво демонстрирующих основы математического анализа – нахождение производной классическим способом как предела отношения приращения функции к приращению аргумента при неограниченном уменьшении последнего. Получим известную формулу для (log_ax)'

$\lim_{\delta \to 0} \frac{(log(x+\delta,a)-logg(x,a)}{\delta} \to \frac{1}{x \cdot ln(a)}$

Дальше >>

Авторизоваться

Введение в программные системы и их разработку

Системы компьютерной математики (СКМ)

12.4.Символьные расчеты в СКМ

Вопросы и ответы