НОУ ИНТУИТ | Рынок как система обслуживания случайных потоков. Лекция 3: Рынок как система с явными потерями

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

Опубликован: 26.10.2016 | Доступ: свободный | Студентов: 405 / 19 | Длительность: 08:16:00

Темы: Экономика, Менеджмент

Специальности: Менеджер, Экономист

|

Вам нравится? Нравится 22 студентам

| Поделиться |

Поддержать курс

| Скачать электронную книгу

3.4. Потери в полнодоступной группе при обслуживании простейшего потока товаров

В предыдущих главах мы уже обсуждали типы потерь в полнодоступной группе при обслуживании простейшего потока товаров. Теперь можно проанализировать эти потери с помощью формулы Эрланга.

Качество обслуживания потока можно оценивать по следующим типам потерь:

$P_{заяв.}$ потери по числу поступивших заявок на поставку товара - $P_{заяв.}$

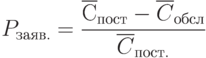$P_{заяв.}=\frac{\overline С_{пост}-\overline C_{обсл}}{\overline C_{пост.}}$

( 3.12)

;

где $\overline C_{пост}$ число поступивших заявок

$\overline C_{обсл}$ - $\tau$ число обслуженных заявок

$\overline C_{потер.}$ - $\tau$ потерянных заявок

б) потери по объему товара -

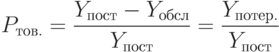$P_{тов.}=\frac{Y_{пост}-Y_{обсл}}{Y_{пост}}=\frac{Y_{потер.}}{Y_{пост}}$

( 3.13)

;

$P_{тов.}=$

где $Y_{пост}$ - величина объема поступившего товара

$Y_{обсл}$ - величина обслуженного товара

$Y_{потер.}$ - величина потерянного товара

в) потери по времени реализации - P_ t .

- определяется как доля времени, в течение, которого заняты все потребители - P_t .

В самом общем случае имеет место соотношение:

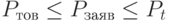
$P_{тов} \leq P_{заяв} \leq P_t$

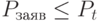$P_{заяв} \leq P_t$ , так как может быть такой случай, когда все потребители заняты, но партия товаров не поступает.

$P_{тов} \leq P_{заяв}$ , так как длительность занятия потребителей повторными предложениями может быть значительно меньше средней длительности потребления.

Рассмотрим соотношение между 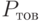$P_{тов}$ , $P_{заяв}$ и P_t для простейшего потока.

Потери по времени.

Вероятности 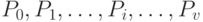можно рассматривать как доли

времени рассматриваемого промежутка, в течение которого заняты 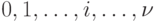$0,1,…, i ,…, \nu$ групп потребителей. Это утверждение представляет собой, так называемую Эргодическую теорему. Это утверждение мы примем без доказательства.

Следовательно, в полнодоступном пучке, на который поступает простейший поток вызовов, потери по времени численно равны вероятности занятия v групп потребителей:

$P_t=E_{ \nu , \nu} (A)=E_{\nu} (A)$
Потери по заявкам.

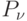Пусть интенсивность поступающего предложения товара на полнодоступные группы потребителей - создаётся числом заявок - $C_{пост}$ поступающим на реализацию партий товаров. Заявки на реализацию партий товаров, которые поступают за долю, составляющую потерянное время (вероятность $P_{\nu}$ ), будут потеряны. Доля потерянных заявок будет равна.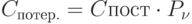

$C_{потер.}=C{пост}\cdot P_{\nu}$ ( 3.14)

Тогда потери по числу поступивших заявок на поставку товара:

$Р_{заяв.}= \frac {C_{потер}}{C_{пост}}=P_{\nu}(Y)=E_{\nu}(Y)$
Определим потери по объему товара - P_{тов.} .

С этой целью определим потери объему товара, обслуженные $\nu$ группами потребителей. Вспомним, что интенсивность предложения обслуженного группами потребителей, численно равна среднему числу одновременно занятых потребителей.

$Р_{заяв.}= \frac {C_{потер}}{C_{пост}}=P_{\nu}(Y)=E_{\nu}(Y)$

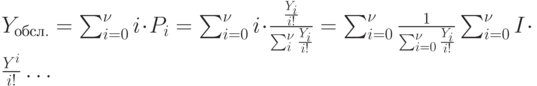
$Y_{обсл.}=\sum_{i=0}^{\nu} i \cdot P_i = \sum_{i=0}^{\nu} i \cdot \frac{\frac{Y_i}{i!}}{ \sum\nolimits_{i}^{\nu} \frac{Y_i}{i!} } = \sum_{i=0}^{\nu} \frac{1}{\sum\nolimits_{i=0}^{\nu}\frac{Y_i}{i!}} \sum_{i=0}^{\nu} I \cdot \frac{Y^i}{i!}…$

Можно показать, что потери по объему товара - $P_{тов} = E_{\nu}(Y )$ . Первый член во второй сумме при равен нулю, поэтому суммирование можно начинать с . Обозначим , тогда при 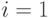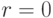, а при $i=\nu$ $r=\nu-1$ :

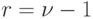$… \frac{Y}{ \sum\nolimits_{i=0}^{\nu} \frac{Y_i}{i!}}\cdot \sum_{i=1}^{\nu}\frac{Y^{i-1}}{(i-1)!}=\frac{Y}{\sum\nolimits_{i=0}^{\nu}} \frac{Y_i}{i!} \cdot \sum_{r=1}^{\nu} \frac{Y^r}{r!}=\frac{Y}{\sum\nolimits_{i=0}^{\nu}\frac{Y_i}{i!}}[\sum_{r=0}^{\nu -1}\frac{Y^r}{r!}+ \frac{Y^{\nu}}{\nu !}- \frac{Y^r}{r!}=…]$

$…\frac{Y}{\sum\nolimits_{i=0}^{\nu}\frac{Y_i}{i!}}[\sum_{r=0}^{\nu}\frac{Y^r}{r!}- \frac{Y^{\nu}}{\nu !}=…]=Y \cdot (1-P_{\nu})=Y-Y \cdot P_{\nu}$

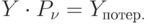
где $Y\cdot P_{\nu} = Y_{потер.}$

Так как $Y_{обсл.}=Y _пост.}-Y_{потер.} , то Y_{ потер.}=Y_{пост.}\cdot p_{\nu}$ .

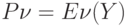
$P \nu =E \nu (Y )$

Таким образом, если полнодоступная группа потребителей обслуживает

простейший поток вызовов, то:

$P_t=P_{тов.} =P_{заяв.}= E_{\nu} (Y) =P$ ( 3.15)

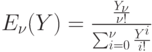
$E_{\nu}(Y)=\frac{\frac{Y_{\nu}}{\nu !}}{ \sum\nolimits_{i=0}^{\nu} \frac{Y^i}{i!} }$

- эта формула, определяющая потери при полнодоступной группе потребителей получила название первой формулы Эрланга.

(Вторая формула Эрланга предназначена для систем с ожиданием).

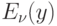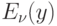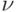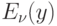Функция $E_{\nu}(y)$ табулирована. Таблицы первой формулы Эрланга построены так, что по числу поставляемых партий товаров, относительному потреблению отыскиваются потери $E_{\nu}(y)$ . Эти таблицы позволяют по двум любым заданным величинам из ${\nu}$ , и $E_{\nu}(y)$ находить третью величину.

Поскольку таблицы предназначены для расчета коммутационных систем, а не рынка, то термины таблицы надо приводить к принятым выше терминам. В табл. 3.1 приведены такие понятия

Таблица 3.1. Термины для применения таблиц первой формулы Эрланга при расчете спроса, предложения и потерь
В таблице	В книге	Обозначение
Нагрузка	Относительное потребление	или
Линии (приборы)	Партии товаров	или $\nu$
Вероятность потерь	Вероятность потерь	$E_{1,\nu}(A)$

Дальше >>

Авторизоваться

Рынок как система обслуживания случайных потоков

Рынок как система с явными потерями

3.4. Потери в полнодоступной группе при обслуживании простейшего потока товаров

Вопросы и ответы