НОУ ИНТУИТ | Рынок как система обслуживания случайных потоков. Лекция 3: Рынок как система с явными потерями

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

Опубликован: 26.10.2016 | Доступ: свободный | Студентов: 406 / 20 | Длительность: 08:16:00

Темы: Экономика, Менеджмент

Специальности: Менеджер, Экономист

|

Вам нравится? Нравится 23 студентам

| Поделиться |

Поддержать курс

| Скачать электронную книгу

3.5. Средняя пропускная способность группы потребителей полнодоступного рынка

Средняя интенсивность предложения, обслуживаемой одной группой потребителей полнодоступного рынка при общем числе потребителей $\nu$ :

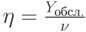$\eta=\frac{Y_{обсл.}}{\nu}$ , $Y_{обсл.} =Y-Y_{потер.} =Y-E_{\nu} (Y) \cdot Y=Y \cdot [1-E_{\nu, \nu} (Y)]$

Записывая выражение для 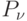$P_{\nu}$ и $P _{\nu-1}$ , легко убедиться, что:

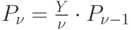$P_{\nu}=\frac{Y}{\nu}\cdot P_{\nu -1}$ или

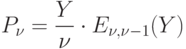$P_{\nu}=\frac{Y}{\nu} \cdot E_{\nu, \nu -1}(Y)$

( 3.16)

Подставляя отсюда в выражение для $Y_{обсл}$ , получим:

$\cdot [1-E_{\downarrow}(\nu , \nu)(Y)]$

$\eta = \frac{E_{\nu , \nu}(Y)}{E_{\nu -1}(Y)}\cdot [1- E_{\downarrow}(\nu , \nu)(Y)]$

( 3.17)

При малой величине потерь:

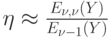
$\eta \approx \frac{E_{\nu , \nu}(Y)}{E_{\nu -1}(Y)}$

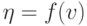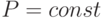
$\eta = f (v)$ при P=const

увеличить изображение
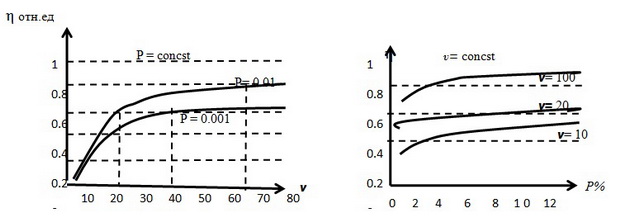
Рис. 3.10. График использования групп потребителей

Рассматривая график можно сделать вывод: для повышения использования групп потребителей необходимо объединять потоки и группы потребителей обслуживающих рынок. Эффект от объединения групп тем выше, чем меньше величина. При v>100 приращение пропускной способности незначительно (кривая почти параллельна оси).

Замечание 1. При 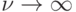$\nu \to \infty$ формула Эрланга может быть заменена формулой Пуассона:

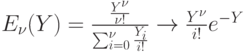$E_{\nu }(Y)=\frac{\frac{Y^{\nu }}{\nu !}}{ \sum\nolimits_{i=0}^{\nu} \frac{Y_i}{i!} } \to \frac{Y^{\nu}}{i!}e^{-Y}$ , так как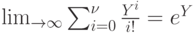 $\lim_{\to \infty } \sum_{i=0}^{\nu } \frac{Y^i}{i !} = e^Y$

Замечание 2. Формула Эрланга 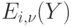$E_{i,\nu} (Y)$ позволяет вычислить вероятность занятия любых (случайных) групп потребителей из $\nu$ групп потребителей.

3.6. Графические зависимости между параметрами первой формулы Эрланга

Потери являются функцией двух переменных 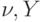$\nu,Y$ :

$P=E_v (Y) = f (\nu,Y)=\frac{\frac{Y^{\nu }}{\nu !}}{\sum\nolimits_{i=0}^{\nu} \frac{Y_i}{i !}}$

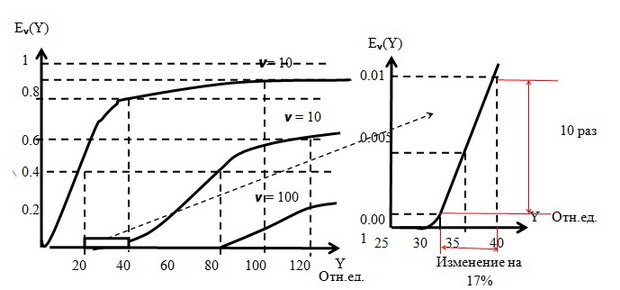
Практический интерес представляет область малых потерь: $0.001 \div 0.01$

Рис. 3.11. График в области малых потерь

Поступающая нагрузка изменилась с 32.5 Отн.ед. до 37.9 Отн.ед., то есть на 17%, а потери возросли в 10 раз! Это область малых потерь.

На практике приходится часто решать задачу, при увеличении поставки на рынок товаров, как должно, изменится число потребителей, чтобы величина потерь оставалась постоянной. Это можно определить только, используя график.

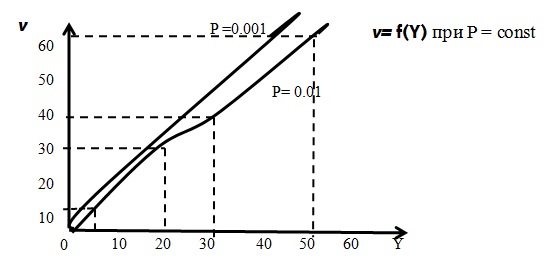
Рис. 3.12. График необходимого числа потребителей при увеличении величины поступающего предложения при сохранении заданной величины потерь

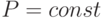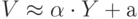При P=const в достаточно большом интервале изменения величины поступающего предложения при Y>10 Отн. Ед. приближённо имеет линейный характер $V \approx \alpha \cdot Y+а$ .

Дальше >>

Авторизоваться

Рынок как система обслуживания случайных потоков

Рынок как система с явными потерями

3.5. Средняя пропускная способность группы потребителей полнодоступного рынка

3.6. Графические зависимости между параметрами первой формулы Эрланга

Вопросы и ответы