Рынок как система с явными потерями

3.1. Постановка задачи

В этой главе мы рассмотрим методы расчёта пропускной способности рынка с полнодоступной группой потребителей в системе с явными потерями.

Мы уже отмечали, что математическая модель рынка характеризуется следующими элементами:

• типом потока предложений товаров,
• дисциплиной обслуживания (с явными потерями или с ожиданием),
• величиной обслуженного предложения и потерями

В этом параграфе рассмотрим простейшую модель:

Задано:

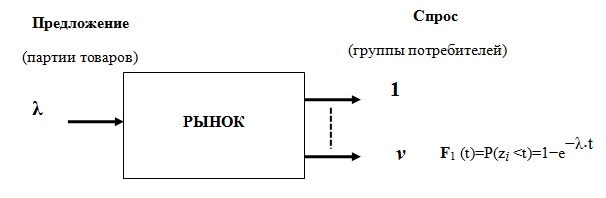
Рынок, на вход которого поступает предложение - партии товаров, а на выходе, которого имеется групп потребителей, каждая из которых обслуживается полнодоступно без приоритетов. Товар может быть приобретён любой из этих групп.

На рынок поступает простейший поток партий товаров

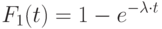( 3.1)

- вероятность поступления товара за время меньше с параметром .

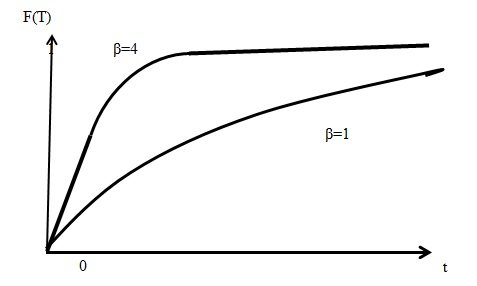
Будем считать, что длительность потребления (длительность занятия любой группы потребителей) - случайная величина и подчиняется показательному закону распределения с параметром (рис. 3.1) .

Рис. 3.1. Показательный закон распределения с параметром

Вероятность того, что за время одна группа потребителей освободится:

,

где - длительность потребления;

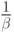- средняя длительность потребления.

Параметр в этом выражении полностью аналогичен параметру показательного закона распределения промежутка 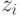между поступлением простейшего потока товаров. Вероятность того, что за время поступит одна партия товара:

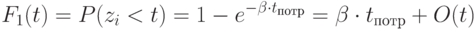( 3.2)

Параметр показывает плотность потока занятий групп потребителей 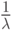- средняя длительность интервала между поставками двух партий товаров).

Аналогично можно рассматривать как плотность потока освобождений потребителей, 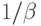- средняя длительность занятия группы потребителей одной партией товара.

В качестве дисциплины обслуживания примем обслуживание партий товаров с явными потерями, то есть при занятости всех потребителей поступивший товар получает отказ в реализации и на рынок не возвращается. Потерянное предложение не оказывает на систему никакого влияния.

Требуется найти вероятность занятия любых линий из числа в фиксированный моментвремени .

Найти 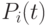- вероятность того, что в момент занято ровно потребителей.

Рис. 3.2. Модель рынка с простейшим поступающим потоком предложений