Рынок как система с явными потерями
3.7. Задачи
Задача 1. Определение интенсивности потребления
Задано: Структурный состав потребителей товара предлагаемой продукции на рынке делится на 5 категорий 
средний объем одной покупки (единиц товара) одним потребителем каждой категории во время наибольшего спроса (ВНС) . 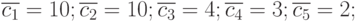 (не учитываются доли покупок с возвратом и другие виды нестандартных действий)
(не учитываются доли покупок с возвратом и другие виды нестандартных действий)
средняя длительность потребления для потребителей разных категорий в днях.  .
.
Максимально возможное потребление одним потребителем товара 20 единиц в месяц.
Рассчитать: интенсивность потребления, поступающих товаров на рассматриваемом рынке от потребителей всех категорий в ВНС.
Решение.
Определим объем товара, который будет приобретен за один месяц всеми категориями покупателей (обслуженное предложение  )
)
 товара
товара
Потребление в отн. единицах равно
 отн.ед.
отн.ед.
Задача. 2. Определение интенсивности поступающего предложения
Задача формулируется следующим образом.
Задано: Структурный состав поставщиков (производителей) товара предлагаемой продукции на рынке делится на 5 категорий 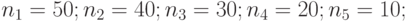
средний объем одной поставки (единиц товара) одним поставщиком каждой категории (ВНС) .
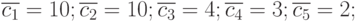
средняя длительность потребления для потребителей разных категорий в днях.

Максимально возможное потребление одним потребителем товара 20 единиц в месяц.
Рассчитать: интенсивность, поступающего предложения товаров на рассматриваемом рынке от потребителей всех категорий в ВНС.
Задача решается, так же как и в предыдущем случае и даёт тот же результат.
Следует специально подчеркнуть, что для определения величины поступающего предложения в относительных единицах применяется величина максимального потребления одним потребителем товара.
Задача 3. Влияние изменения величины предложения на величину потерь в группах потребителей
Полнодоступные группы потребителей  ,
,  и
и  обслуживают простейшие потоки вызовов. На группу потребителей
обслуживают простейшие потоки вызовов. На группу потребителей  в выходной и будний дни поступает предложение интенсивностью
в выходной и будний дни поступает предложение интенсивностью 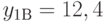 отн.ед,
отн.ед, 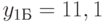 отн.ед. на группу
отн.ед. на группу 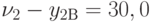 отн.ед,
отн.ед, 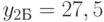 отн.ед. на пучок
отн.ед. на пучок 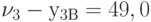 отн.ед,
отн.ед, 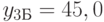 отн.ед.
отн.ед.
Определить:
а) потери по числу поступивших заявок на поставку товара  , потери по объему товара
, потери по объему товара  , потери по времени реализации -
, потери по времени реализации - 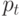 .
.
в группах  ,
, 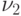 и
и 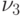 ;
;
б) соотношения между относительными величинами изменения потерь и поступающего предложения в каждой из этих групп.
Решение:
а) Согласно (3.15)  . По таблицам первой формулы Эрланга находим:
. По таблицам первой формулы Эрланга находим:
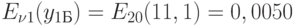 ;
; 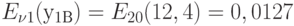 ;
;
 ;
; 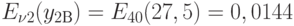 ;
;
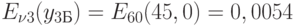 ;
; 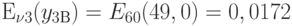 .
.
б) Относительные величины изменения потерь  и изменения предложения
и изменения предложения
 определяются из соотношений
определяются из соотношений
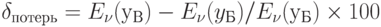

При 
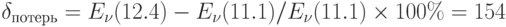

Аналогично определяем:
при 
при  .
.
Соотношения между \delta _{потерь} и \delta _{предлож} для групп  ,
, 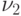 и
и 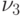 соответственно составляют:
соответственно составляют:
 ;
;
 ;
;
 .
.
Следует подчеркнуть, что при рассмотренных в этой задаче значениях предложениям, увеличение поступающего предложения примерно на 10% (11.1%, 9.1%, 8,9%)приводит к увеличению потерь в 2,5-3 раза, т. е. потери возрастают в 10-25 раз быстрее по сравнению с величиной интенсивности поступающей нагрузки.
Задача 4. Изменение числа групп потребления для сохранениния величины потерь
От трех групп поставщиков поступают товары, образующие простейшие потоки и создающие потоки предложений, интенсивности которых составляют 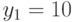 ,
,  и
и 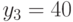 Эрл. Эти потоки товаров обслуживаются полнодоступными группами потребителей.
Эрл. Эти потоки товаров обслуживаются полнодоступными группами потребителей.
Определить: а) требуемое число групп потребления, если потери не должны превышать  и
и 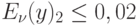 ;
;
б) соотношения между относительными величинами приращения числа групп потребителей и возможностей увеличения интенсивности поступающей нагрузки при сохранении заданного качества обслуживания.
Решение:
а) По таблицам формулы Эрланга при заданных величинах интенсивности поступающего предложения  и заданных значениях потерь
и заданных значениях потерь  определяются требуемые емкости групп потребителей:
определяются требуемые емкости групп потребителей:
| Заданная величина потерь | Число групп потребителей, при интенсивности поступающего предложения, в отн.ед. | ||
Число потребителей 
|
Число потребителей 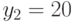
|
Число потребителей 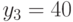
|
|
 |
 |
 |
 |
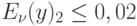 |
 |
 |
 |
б) Относительные величины приращения числа групп потребителей 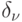 и увеличения интенсивности поступающего предложения \delta _{предлож.} определяются из соотношений:
и увеличения интенсивности поступающего предложения \delta _{предлож.} определяются из соотношений:
\delta _{\nu}= \nu _i - \nu _{i-1}/\nu _{i-1} \times 100\% ; \delta _{предлож}= y_i - y_{i-1}/y_{i-1} \times 100\% i=2 или 3
\delta _{предлож1}= y_2 - y_1/y_1 \times 100\% \delta _{предлож2}= y_3 - y_2/y_2 \times 100\%
При 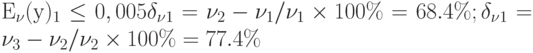 ;
;
При 
 ;
; 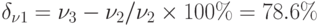 .
.
Решение этой задачи показывает, условия сохранения заданной величины потерь:
а) если на полнодоступную групп потребителей поступают нагрузки интенсивностью 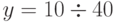 отн.ед., то в области малых потерь увеличение потерь с
отн.ед., то в области малых потерь увеличение потерь с  до
до 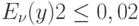 (в 4 раза) позволяет уменьшить требуемые емкости групп потребителей только примерно на 10%;
(в 4 раза) позволяет уменьшить требуемые емкости групп потребителей только примерно на 10%;
б) в области малых потерь и относительно небольших значений интенсивности поступающего предложения (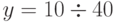 отн.ед) емкости требуемых групп потребителей возрастают медленнее по сравнению с величиной поступающего предложения. При фиксированной величине потерь увеличение интенсивности поступающей нагрузки в 2 раза требует увеличения емкости групп потребителей на 65-80 %.
отн.ед) емкости требуемых групп потребителей возрастают медленнее по сравнению с величиной поступающего предложения. При фиксированной величине потерь увеличение интенсивности поступающей нагрузки в 2 раза требует увеличения емкости групп потребителей на 65-80 %.
