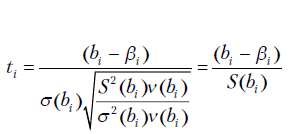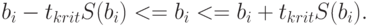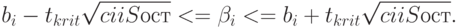|
В дисциплине "Основы эконометрики" тест 6 дается по теме 7. |
Множественная регрессия
3.5. Доверительные интервалы для коэффициентов регрессии и проверка гипотезы об их значимости
В условиях Гаусса - Маркова оценки 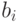 имеют нормальное распределение и, как установлено ранее,
имеют нормальное распределение и, как установлено ранее, 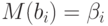 . Обозначим дисперсию этих оценок
. Обозначим дисперсию этих оценок 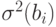 . Тогда случайная величина
. Тогда случайная величина 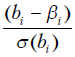 является нормированной нормально распределенной величиной, т.е. имеет нулевое математическое ожидание и единичную дисперсию. Вместе с тем можно показать, что отношение
является нормированной нормально распределенной величиной, т.е. имеет нулевое математическое ожидание и единичную дисперсию. Вместе с тем можно показать, что отношение 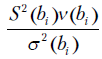 имеет распределение
имеет распределение 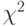 . Поэтому выражение
. Поэтому выражение
имеет распределение Стьюдента с числом степеней свободы 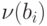 . Если
. Если  выбранный уровень значимости, то по таблицам распределения определяем значение
выбранный уровень значимости, то по таблицам распределения определяем значение  , для которого неравенство
, для которого неравенство 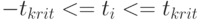 справедливо с вероятностью
справедливо с вероятностью 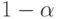 . Из равенства (3.21) и последнего неравенства получаем
. Из равенства (3.21) и последнего неравенства получаем
Учитывая соотношение (3.15), окончательно имеем
Оценка неравенства (3.24) позволяет проверить гипотезу о равенстве нулю неизвестного параметра 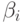 . Если эта гипотеза справедлива, то выборочная оценка
. Если эта гипотеза справедлива, то выборочная оценка 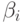 может отличаться от нуля лишь за счет случSайных возмущений. Рассмотрим выражение (3.22) при
может отличаться от нуля лишь за счет случSайных возмущений. Рассмотрим выражение (3.22) при 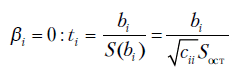 . Определив по таблицам распределения
. Определив по таблицам распределения  по заданному уровню значимости a и известному числу степеней свободы
по заданному уровню значимости a и известному числу степеней свободы 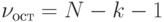 , соответствующему
, соответствующему 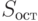 , делаем вывод:
, делаем вывод:
- если
 , то коэффициент
, то коэффициент 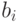 значим, т.е.
значим, т.е.  ;
; - если
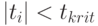 , то коэффициент
, то коэффициент 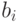 незначимо отличается от нуля и соответствующим слагаемым в регрессионной модели, возможно, следует пренебречь.
незначимо отличается от нуля и соответствующим слагаемым в регрессионной модели, возможно, следует пренебречь.