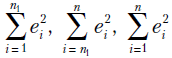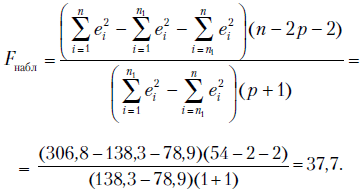|
В дисциплине "Основы эконометрики" тест 6 дается по теме 7. |
Множественная регрессия
3.12. Тест Чоу для проверки структурных изменений модели
Если исследователь предполагает, что за время наблюдений произошли резкие структурные изменения в виде связей между зависимой и независимыми переменными, то для проверки этой гипотезы используют тест Чоу. В этом случае строятся три регрессионные модели: первая по наблюдениям, проведенным до изменений, вторая по наблюдениям после происшедших изменений в структуре связей, а третья по всей выборке наблюдений. Нулевая гипотеза состоит в предположении о равенстве истинных соответствующих параметров регрессии для всех моделей. Нулевая гипотеза отвергается при уровне значимости \alpha , если наблюдаемая  -статистика
-статистика
где
 |
- | число переменных в модели; |
| - | суммы квадратов остатков моделей, построенных по наблюдениям, проведенным до изменений, после изменений и по всей выборке. |
Рассмотрим пример. Пусть  временной ряд урожайности зерновых культур в России, график которого представлен на рис. 3.1.
временной ряд урожайности зерновых культур в России, график которого представлен на рис. 3.1.
Следует проверить гипотезу об изменении в тенденции поведения ряда, которое произошло после распада СССР, т.е. после 1991 г., вследствие ухудшения снабжения сельскохозяйственного производства горюче-смазочными материалами (ГСМ), удобрениями, сельскохозяйственной техникой.
Первая выборка включает все наблюдения за период 1948-2001 гг. При этом уравнение регрессии имеет вид  . То есть в среднем урожайность зерновых в России повышалась на 0,18 ц/га в год. Сумма квадратов остатков для этого уравнения равна
. То есть в среднем урожайность зерновых в России повышалась на 0,18 ц/га в год. Сумма квадратов остатков для этого уравнения равна  О качестве модели можно судить по табл. 3.13.
О качестве модели можно судить по табл. 3.13.
Таблица 3.13
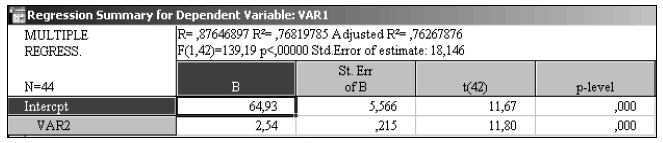
Вторая выборка состоит из наблюдений за 1948-1991 гг. Уравнение регрессии на этом участке имеет следующий вид:  (табл. 3.14).
(табл. 3.14).
Таблица 3.14
Сумма квадратов остатков при этом равна 
Получим уравнение для оставшейся части наблюдений за 1991-2001 гг. (табл. 3.15). Имеем  .
.
Таблица 3.15
Сумма квадратов остатков при этом равна
Наблюдаемая  -статистика Чоу равна
-статистика Чоу равна
При 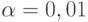

Нулевая гипотеза об отсутствии изменения в тенденции поведения ряда урожайности в России после распада СССР уверенно опровергается на 1%-ном уровне значимости.
3.13. Выбор модели оптимальной сложности. Критерии Акайке и Шварца
При построении модели, адекватно описывающей изучаемый процесс в экономике, очень важную роль играет анализ правильности ее спецификации. Отрицательно на объясняющих свойствах модели сказывается как отсутствие значимой переменной, так и избыточное присутствие незначимой объясняющей переменной.
В случае когда в модель не включена существенная переменная (существенной называют переменную, которая должна быть в модели согласно правильной теории), наблюдаются следующие последствия:
- исчезает возможность правильной оценки и интерпретации уравнений;
- коэффициенты при оставшихся переменных становятся смещенными;
- стандартные ошибки коэффициентов и t-статистики некорректны и поэтому не могут быть использованы для суждения о качестве подгонки предлагаемой модели.
Предположим, к примеру, что из модели  исключена переменная
исключена переменная  . Тогда в новой спецификации фактически рассматривается модель
. Тогда в новой спецификации фактически рассматривается модель  .
.
Если объясняющие переменные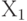 и
и коррелированы, то нарушается предпосылка теоремы Гаусса - Маркова о некоррелированности случайного члена и регрессоров, поскольку в этом случае между
коррелированы, то нарушается предпосылка теоремы Гаусса - Маркова о некоррелированности случайного члена и регрессоров, поскольку в этом случае между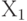 и
и  существует ненулевая корреляция. Оценки, полученные по методу наименьших квадратов для данной модели, уже не являются эффективными среди линейных оценок.
существует ненулевая корреляция. Оценки, полученные по методу наименьших квадратов для данной модели, уже не являются эффективными среди линейных оценок.
Они даже не являются несмещенными, поскольку для МНК-оценки коэффициента  в этом случае получаем:
в этом случае получаем: 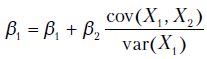 .
.
Наблюдается смещение, равное
Включение несущественной переменной в модель не приводит к смещению оценок коэффициентов, но появляется другой недостаток - растут стандартные ошибки коэффициентов. Оценки становятся статистически незначимыми.
Если точная спецификация модели неизвестна (что практически всегда и бывает), то пользуются критериями, позволяющими выбирать из некоторого множества моделей наилучшую модель.
Наиболее распространенными являются критерий Шварца и критерий Акайке. Они позволяют выбирать наилучшую модель из множества различных спецификаций и численно построены так, чтобы учесть влияние на качество подгонки модели двух противоположных тенденций.
При добавлении переменных в модель качество подгонки в общем случае увеличивается. Заметим, что число регрессоров должно быть разумным, чтобы не вызвать "искусственной подгонки" зависимой переменной. Вместе с тем недостаточное количество переменных, включаемых в модель, дает большую стандартную ошибку, что ведет к снижению качества подгонки.
Рассматриваемые критерии находят по формулам
где
Значение в этом случае равно числу независимых переменных, включая свободный член. Таким образом, если в модели присутствует два регрессора и свободный член, то число ограничений на степени свободы будет равно трем.
в этом случае равно числу независимых переменных, включая свободный член. Таким образом, если в модели присутствует два регрессора и свободный член, то число ограничений на степени свободы будет равно трем.
Первое слагаемое представляет собой штраф за большую дисперсию, второе - штраф за использование дополнительных переменных. Критерии рассчитываются для каждой рассматриваемой спецификации. При сравнении двух типов моделей предпочтение отдается спецификации, которая имеет наименьшие значения критериев.
Рассмотрим пример использования информационных критериев при выборе наилучшей спецификации модели.
В качестве исходных данных возьмем временной ряд длиной 20 наблюдений. Будем подгонять этот ряд линейными регрессиями, в которых регрессоры являются полиномами различных степеней - . Наша задача - выбрать оптимальную степень наибольшего полинома. Для сравнения моделей с различными степенями полиномов воспользуемся критериями Акайке и Шварца. Модель, показывающую наименьшие значения критериев, будем считать оптимальной.
. Наша задача - выбрать оптимальную степень наибольшего полинома. Для сравнения моделей с различными степенями полиномов воспользуемся критериями Акайке и Шварца. Модель, показывающую наименьшие значения критериев, будем считать оптимальной.
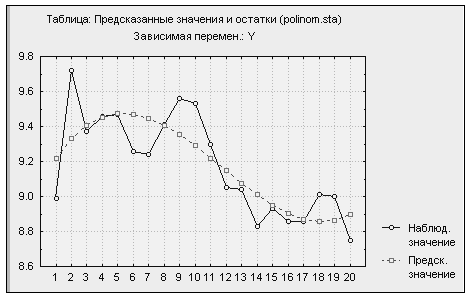
Для регрессии  значения критериев и коэффициенты полинома представлены в табл. 3.16, а график наблюдаемых и предсказанных значений для
значения критериев и коэффициенты полинома представлены в табл. 3.16, а график наблюдаемых и предсказанных значений для 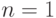 - на рис. 3.2.
- на рис. 3.2.
Таблица 3.16
Для регрессии  значения критериев и коэффициенты полинома представлены в табл. 3.17, а график наблюдаемых и предсказанных значений для
значения критериев и коэффициенты полинома представлены в табл. 3.17, а график наблюдаемых и предсказанных значений для 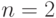 - на рис. 3.3.
- на рис. 3.3.
Таблица 3.17
Для регрессии  значения критериев и коэффициенты полинома представлены в табл. 3.18, а график наблюдаемых и предсказанных значений для
значения критериев и коэффициенты полинома представлены в табл. 3.18, а график наблюдаемых и предсказанных значений для 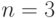 - на рис. 3.4.
- на рис. 3.4.
Таблица 3.18
Для регрессии  значения критериев и коэффициенты полинома представлены в табл. 3.19, а график наблюдаемых и предсказанных значений для
значения критериев и коэффициенты полинома представлены в табл. 3.19, а график наблюдаемых и предсказанных значений для 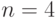 - на рис. 3.5.
- на рис. 3.5.
Таблица 3.19
Для регрессии  значения критериев и коэффициенты полинома представлены в табл. 3.20, а график наблюдаемых и предсказанных значений для
значения критериев и коэффициенты полинома представлены в табл. 3.20, а график наблюдаемых и предсказанных значений для 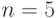 - на рис. 3.6.
- на рис. 3.6.
Таблица 3.20
Для регрессии  значения критериев и коэффициенты полинома представлены в табл. 3.21, а график наблюдаемых и предсказанных значений для
значения критериев и коэффициенты полинома представлены в табл. 3.21, а график наблюдаемых и предсказанных значений для  - на рис. 3.7.
- на рис. 3.7.
Таблица 3.21
Для регрессии  значения критериев и коэффициенты полинома представлены в табл. 3.22, а график наблюдаемых и предсказанных значений для
значения критериев и коэффициенты полинома представлены в табл. 3.22, а график наблюдаемых и предсказанных значений для  - на рис. 3.8.
- на рис. 3.8.
Таблица 3.22
Для регрессии  значения критериев и коэффициенты полинома представлены в табл. 3.23, а график наблюдаемых и предсказанных значений для
значения критериев и коэффициенты полинома представлены в табл. 3.23, а график наблюдаемых и предсказанных значений для  - на рис. 3.9.
- на рис. 3.9.
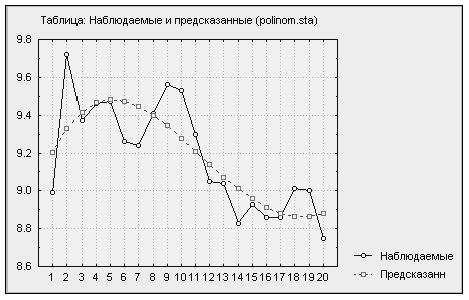
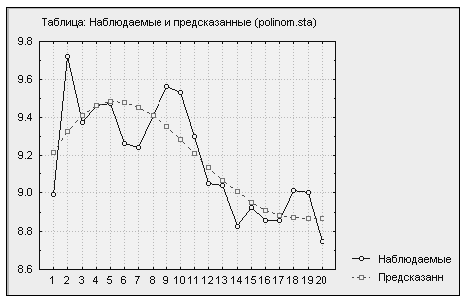
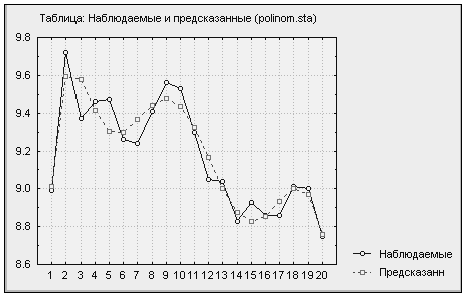
Таблица 3.23. Наблюдаемые и предсказанные(polinom.sta)
Сравнительный график предсказаний для моделей со степенями полиномов  и
и  представлен на рис. 3.10.
представлен на рис. 3.10.
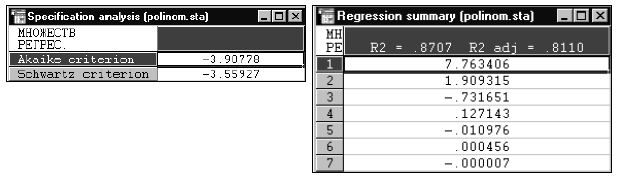
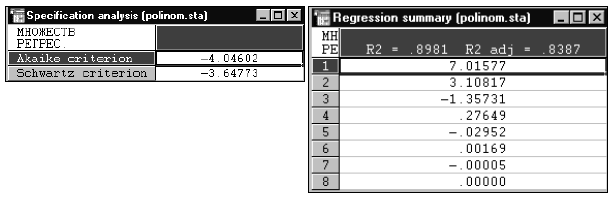
Результаты показывают, что минимум значений критериев Акайке и Шварца наблюдается при самой высокой степени полинома, равной семи. Отсюда вывод: при подгонке исследуемого ряда целесообразно использовать спецификацию с наивысшей степенью полинома, равной семи.
Дополнительным доводом в пользу такого выбора спецификации может служить значение скорректированного 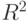 , которое является наибольшим из всех рассматриваемых.
, которое является наибольшим из всех рассматриваемых.
Графический анализ качества подгонки полиномами неизвестной функции дает следующий результат: при повышении степени полинома с 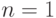 до
до  улучшение объясняющих свойств модели можно наблюдать визуально. На изображенных графиках (см. рис. 3.2-3.10) предсказанные значения приближаются к реальным данным с увеличением степени полинома. При использовании полинома восьмой степени качество подгонки практически не улучшается. На приведенном сравнительном графике предсказаний для моделей со степенями полинома
улучшение объясняющих свойств модели можно наблюдать визуально. На изображенных графиках (см. рис. 3.2-3.10) предсказанные значения приближаются к реальным данным с увеличением степени полинома. При использовании полинома восьмой степени качество подгонки практически не улучшается. На приведенном сравнительном графике предсказаний для моделей со степенями полинома  и
и  (см. рис. 3.10) графики предсказанных значений сливаются, следовательно, использование полинома восьмой степени избыточно и практически не улучшает прогнозных свойств модели. Этот вывод подтверждается и ростом значения критерия Акайке.
(см. рис. 3.10) графики предсказанных значений сливаются, следовательно, использование полинома восьмой степени избыточно и практически не улучшает прогнозных свойств модели. Этот вывод подтверждается и ростом значения критерия Акайке.
Контрольные вопросы
- Напишите линейную модель регрессии с
 -факторами.
-факторами. - Какая матрица называется ковариационной матрицей случайного вектора
 , а какая - корреляционной? В чем их отличие?
, а какая - корреляционной? В чем их отличие? - Каково условие однородности (гомоскедастичности) наблюдений?
- Как посредством МНК получают систему нормальных уравнений? С какой целью составляется и решается система нормальных уравнений МНК?
- Приведите формулу расчета коэффициентов регрессионного уравнения в методе наименьших квадратов.
- Докажите несмещенность МНК-оценок коэффициентов модели.
- Выведите формулу расчета дисперсий и средних квадратических ошибок МНК-коэффициентов модели. Что собой представляет матрица дисперсий-ковариаций векторов-столбцов матрицы наблюдений?
- Как оценивается качество уравнения регрессии с помощью абсолютной и относительной ошибки аппроксимации?
- Дайте определение коэффициента детерминации.
- Как проводится дисперсионный анализ качества модели в случае многих факторов?
- Как проверяется значимость коэффициентов регрессии?
- Приведите формулы для расчета доверительного интервала функции регрессии и для индивидуальных значений зависимой переменной.
- Почему коэффициент детерминации во многих случаях не может помочь при определении числа включаемых в модель переменных?
- Дайте определение частного коэффициента корреляции. Какова его роль в процедуре шаговой регрессии последовательного включения (исключения) переменных?
- В чем заключается проблема мультиколлинеарности факторов?
- Опишите способы устранения мультиколлинеарности, в частности процедуру гребневой регрессии (ридж-регрессии).
- Расскажите о методе главных компонент, эффективной процедуре борьбы с мультиколлинеарностью.
- Какие переменные называются фиктивными, манекенными? Чем вызвана необходимость использования фиктивных переменных?
- Расскажите о тесте Чоу проверки структурной однородности модели.
- Как осуществляется выбор моделей оптимальной сложности на основе критериев Акайке и Шварца?