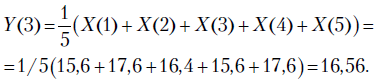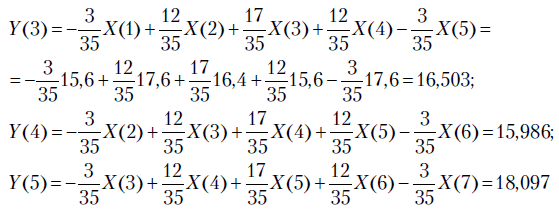Лабораторная работа № 7: Сглаживание временного ряда

Требуется сгладить временной ряд методами:

1. простой скользящей средней;
2. взвешенной средней:
   1. выбором весов в разложении бинома;
   2. с выбором весов из уравнения квадратичной регрессии;
3. простой экспоненциальной средней.

Отчет по лабораторной работе № 7

Задан ряд показателей урожайности зерновых культур в целом по России (ц/га) за 1984-1999 гг.: 15,6; 17,6; 16,4; 15,6; 17,6; 20,3; 15,8; 18,8; 17,9; 15,6; 12,5; 14,0; 17,8; 10,4; 10,6.

Метод простой скользящей средней. Сглаживание производится по формуле (6.2)

Выберем ширину интервала сглаживания .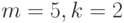

Расчеты будем проводить по рекуррентной формуле

Но вначале найдем Y(3):

Тогда:

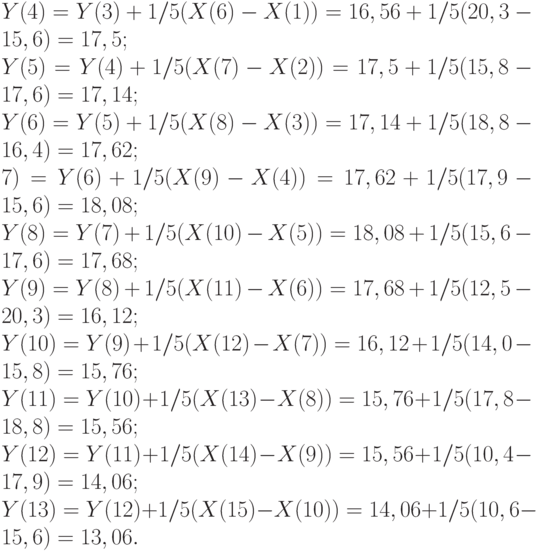
Полученные результаты запишем в таблицу.

Методы взвешенной средней. В случае биномиального сглаживания расчет производится по формулам 6.4-6.7.

При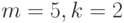

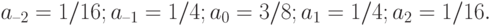
Тогда:

и т.д. Наконец,

Результаты вычислений заносим в четвертую графу таблицы.

В современных вычислительных пакетах сглаживание по биному не представляет труда. Например, в пакете STATISTICA программа сглаживания нашего ряда выглядит следующим образом:

RandomAccess;

			For i: = 3 to 13 do
			begin
			V(i, 4): = (1/16) · V(i - 2,2) + (1/4) · V(i - 1,2) + (3/8) · V(i, 2) + (1/4) · V(i + 1,2) + (1/16) · V(i + 2,2);
		end.

Для расчета сглаженных средних по квадратичной регрессии используется та же формула, но с другими весами (см. (6.10).

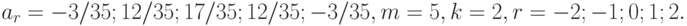
Тогда:

и т.д. Наконец,

Кроме того, используя формулы (6.14)-(6.21), рассчитаем :

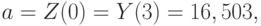
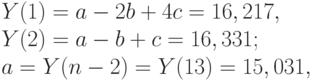
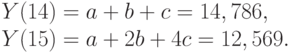
Результаты расчетов занесем в пятую графу таблицы.

Метод простой экспоненциальной средней. Выберем 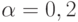(середину интервала [0; 0,3]). Заметим, что, пользуясь пакетом STATISTICA, следует выбирать оптимальное a из интервала [0; 1]. Для расчета применим рекуррентную формулу (6.24)

Получаем:

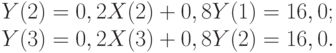
и т.д. Результаты занесем в шестую графу таблицы.

Таблица 1

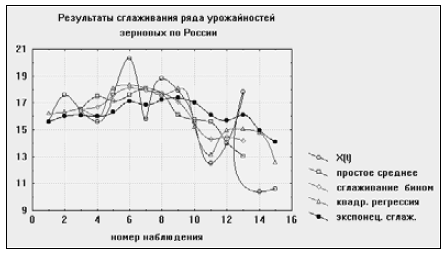
Результаты сглаживания представим в виде графика.

Рис. 1.

Как можно видеть из рисунка, качество сглаживания всех методов удовлетворительное. Но в целях дальнейшего прогноза ряда метод экспоненциального сглаживания представляется более предпочтительным.