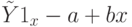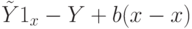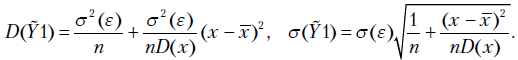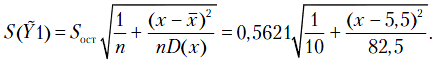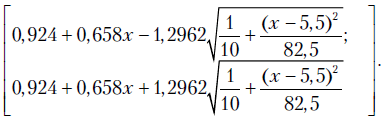Парный регрессионный анализ

2.4. Точечный и интервальный прогнозы по уравнению парной регрессии

Для получения интервалов прогноза по линейному уравнению регрессии преобразуем с учетом формул (2.5) уравнение

(2.22)

в уравнение

(2.23)

Из формулы (2.1) вытекает, что 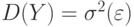, из свойств дисперсии среднего имеем 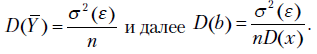Следовательно,

(2.24)

Перейдя от стандартного теоретического отклонения к стандартной выборочной ошибке, получаем

(2.25)

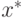Выберем некоторый уровень надежности \gamma , например, равный 0,95, т.е. 95%-ный уровень надежности прогноза. Тогда доверительный интервал для расчета прогноза при данном значении рассчитывается по формуле

(2.26)

где 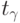находят по таблицам Стьюдента (Приложение 4) для заданного и 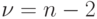(в случае парной регрессии). Например, пр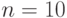и и 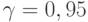получаем 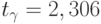. В нашем примере 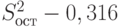. Следовательно, 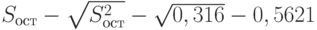. Далее

Получаем окончательную формулу для интервала прогноза :

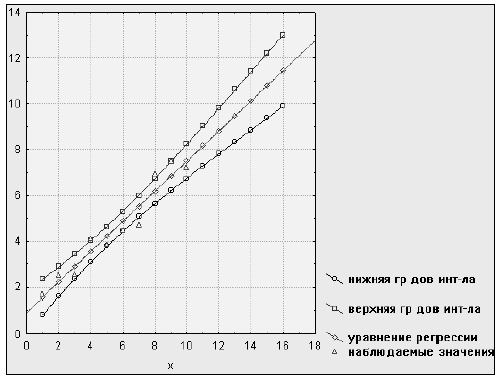
Построим соответствующие графики, используя возможности пакета STATISTICA, на участке [0; 16] (рис. 2.3).

Рис. 2.3.